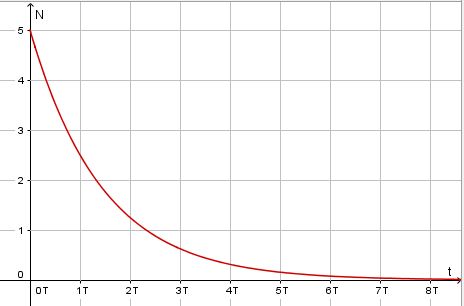
Ph9 Zerfallsgesetz
|
Merke:
In einem bestimmten Zeitraum Wann ein bestimmter Kern zerfällt, kann nicht vorhergesagt werden, er zerfällt zufällig. Man weiß nur, dass bei einer sehr großen Anzahl von radioaktiven Kernen nach Die Aktivität A eines radioaktiven Stoffes ist die Anzahl der Kernzerfälle pro Zeitintervall. Es ist |

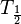 ist die Hälfte aller radioaktiven Kerne zerfallen.
ist die Hälfte aller radioaktiven Kerne zerfallen. 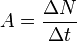 , wobei
, wobei 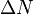 die Anzahl der zerfallenen Kerne ist, die in der Zeit
die Anzahl der zerfallenen Kerne ist, die in der Zeit 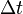 zerfallen sind.
zerfallen sind. .
.

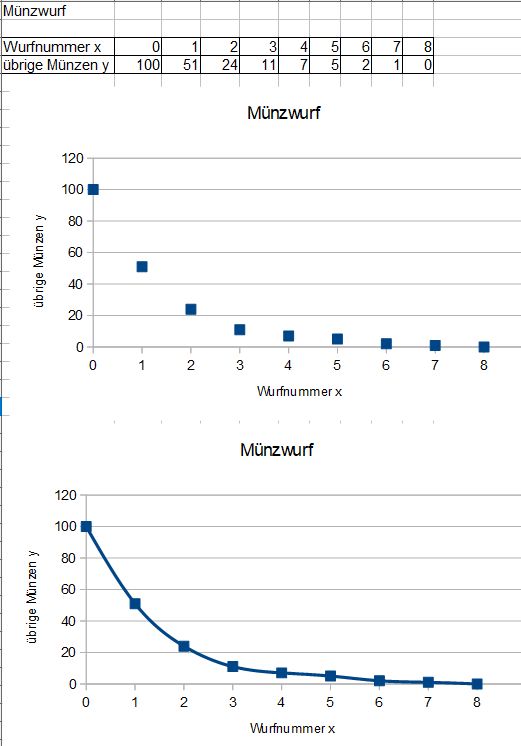
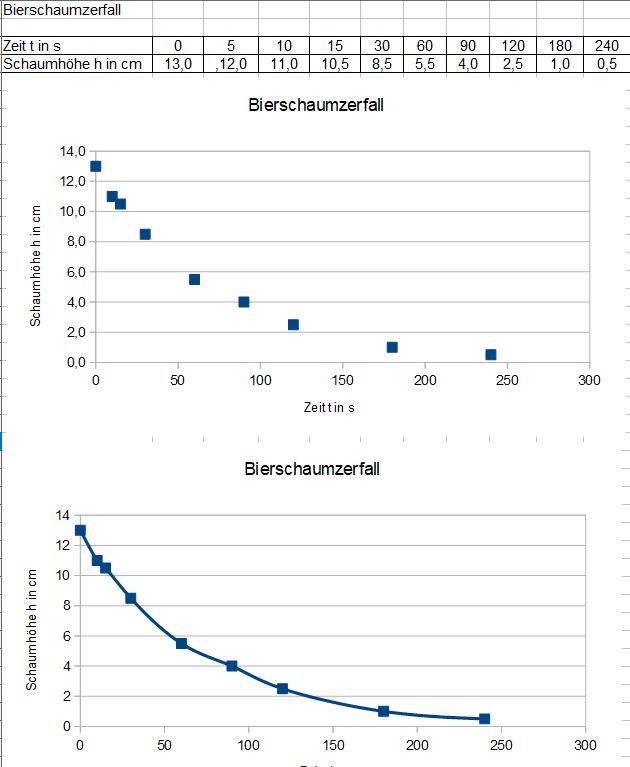
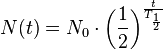
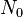 die zur Zeit t = 0s vorhandene Anzahl nicht zerfallener Kerne und
die zur Zeit t = 0s vorhandene Anzahl nicht zerfallener Kerne und