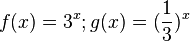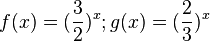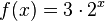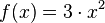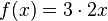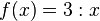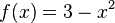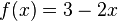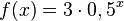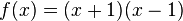Die Funktion 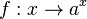
Verändere die Basis a und beobachte die Auswirkungen auf den Verlauf des Graphen.
Notiere die Antworten auf folgende Fragen:
1. Für welche Werte der Basis a ist die Funktion streng monoton steigend und für welche Werte streng monoton fallend?
2. Gibt es einen Wert für a, sodass die Funktion konstant ist?
3. Gibt es Werte für a, sodass der Graph der Funktion unterhalb der x-Achse verläuft?
4. Gibt es für alle Graphen einen gemeinsamen Punkt?
[Lösung anzeigen][Lösung ausblenden]
1. Für 0 < a < 1 ist die Exponentialfunktion streng monoton fallend, für a > 1 ist sie streng monoton steigend.
2. Für a = 1 ist die Funktion konstant.
3. Der Graph der Funktion verläuft für alle Werte von a oberhalb der x-Achse.
4. Alle Graphen gehen durch den Punkt (0:1).
Die Funktion 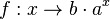
Verändere mit den Schiebereglern den Faktor b und die Basis a.
Notiere die Antworten auf folgende Fragen:
1. Wie beeinflusst der Faktor b den Verlauf des Graphen?
2. Wie hängen die Koordinaten des Schnittpunkts des Graphen mit der y-Achse von den Parametern b und a ab?
[Lösung anzeigen][Lösung ausblenden]
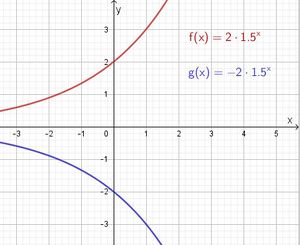
1. Wenn der Faktor b negativ ist, verläuft der Graph der Funktion unterhalb der x-Achse.
2. Der Graph der Funktion f mit f(x) = b·a
x geht stets durch den Punkt (0;b).
1. Drucke dieses Blatt aus und zeichne die Graphen. Übberprüfe deine Zeichnung mit GeoGebra.
2. Ordne richtig zu.
Zusammenfassung
1. Verifiziere die Aussagen des Merksatzes mit Hilfe des Applets.
2.a) Welche Bedeutung hat der Wert des Parameters a für den Verlauf des Graphen?
b) Was ist für a =1?
c) Welche Bedeutung hat der Wert von b für den Verlauf des Graphen?
[Lösung anzeigen][Lösung ausblenden]
2.a) Der Parameter a gibt das Wachstum an. Ist 0 < a < 1, so hat man eine exponentielle Abnahme, für 1 < a eine exponentielle Zunahme.
0 < a < 1: Je kleiner a ist, desto schwächer fällt der Graph. Nähert sich a dem Wert 1, dann fällt der Graph steiler.
1 < a: Je größer a wird, desto steiler wird der Graph.
b) Für a = 1 hat man die konstante Funktion f(x) = b·1x = b·1 = b.
c) Der Parameter b gibt den Startwert bei x = 0 an. Veränderung von b streckt bzw. staucht den Graph der Exponentialfunktion
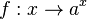
, wenn 0 < b < 1 wird er nach unten in y-Richtung gestaucht, wenn 1 < b ist nach oben in y-Richtung gestreckt. Wenn b negativ ist erfolgt eine Spiegelung an der x-Achse.
Aufgaben
[Lösung anzeigen][Lösung ausblenden]
1. siehe Applet 1 nach der Lösung.
Die Graphen sind achsensymmetrisch zur y-Achse.
Begründung: Ersetzt man x durch -x, dann ist 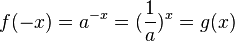
2.a) Exponentialfunktion
b) quadratische Funktion
c) lineare Funktion
d) Bruchfuntkion
e) quadratische Funktion
f) lineare Funktion
g) Exponentialfunktion
h) quadratische Funktion
Graphen siehe Applet 2 nach der Lösung
Applet 1:
Applet 2:
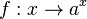
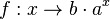
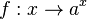 , wenn 0 < b < 1 wird er nach unten in y-Richtung gestaucht, wenn 1 < b ist nach oben in y-Richtung gestreckt. Wenn b negativ ist erfolgt eine Spiegelung an der x-Achse.
, wenn 0 < b < 1 wird er nach unten in y-Richtung gestaucht, wenn 1 < b ist nach oben in y-Richtung gestreckt. Wenn b negativ ist erfolgt eine Spiegelung an der x-Achse.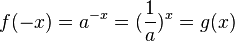

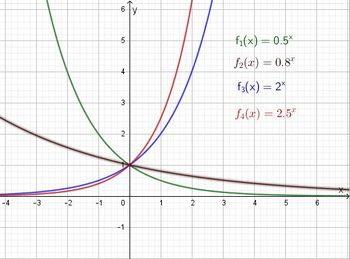
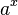 ist stets positiv.
ist stets positiv.
 mit
mit 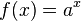 und
und  mit
mit 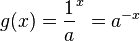 lliegen symmetrisch bezüglich der y-Achse.
lliegen symmetrisch bezüglich der y-Achse.
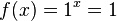 konstant,
konstant,