Bruchterme und Bruchgleichungen

Hinweis:

Der Link öffnet sich in einem eigenen Fenster, wenn du beim Anklicken mit der Maus 

die Shift-Taste drückst.

Bruchterme

• Auf dieser Seite wird erklärt wie man Bruchterme kürzt, erweitert, Bruchterme addiert, subtrahiert, multipliziert und dividiert.

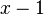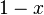• Beachte, dass Terme wie $x-1$ und $1-x$ sehr ähnlich sind und du kannst den einen Term durch Ausklammern von 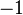$-1$ in den anderen überführen: $1-x=-(-1+x)=-(x-1)$.
  

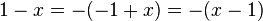Das Minuszeichen vom Nenner kannst du auch vor den Bruch schreiben! 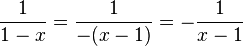$\frac{1}{1-x}= \frac{1}{-(x-1)} = - \frac{1}{x-1}$
Dann ist 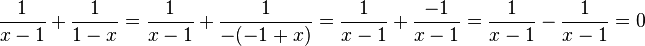$\frac{1}{x-1}+\frac{1}{1-x}=\frac{1}{x-1}+\frac{1}{-(-1+x)}=\frac{1}{x-1}+\frac{-1}{x-1}=\frac{1}{x-1}-\frac{1}{x-1}=0$

• Beachte außerdem, dass du nie aus Summen kürzen darfst!
  

Beispiel 1: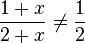$\frac{1+x}{2+x} \not= \frac{1}{2}$ , Beispiel 2: 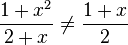$\frac{1+x^2}{2+x} \not= \frac{1+x}{2}$, Beispiel 3: 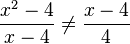$\frac{x^2-4}{x-4} \not= \frac{x-4}{4}$ x darf man nicht kürzen!
Beispiel 4: 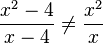$\frac{x^2-4}{x-4} \not= \frac{x^2}{x}$, Beispiel 5: 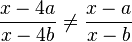$\frac{x-4a}{x-4b} \not= \frac{x-a}{x-b}$ 4 darf man nicht kürzen!

Kürzen und Erweitern, Bruchterme,
von TheSimpleMaths: Bruchterme vereinfachen, Grundlagen, Tipps und Tricks

Aufgaben:
Du brauchst Stift und Papier und rechnest selbst. Wenn du fertig bist, kannst du deine Lösung vergleichen.

Kürzen
Addition
Multiplikation

Binomische_Formeln - Binomische Formeln sind oft hilfreich beim Rechnen mit Bruchtermen.

Bruchgleichungen

• Eine ausführliche Erklärung zu Bruchtermen und Bruchgleichungen mit Umformungen und Rechenbeispielen findest du auf dieser Seite

So löst man Bruchgleichungen

Bruchgleichungen von TheSimpleMaths, Beispiel, Bruchgleichungen, schwierigere Aufgabe

Aufgaben:
Aufgaben mit Lösungen - Bearbeite die Aufgaben 1 und 2!
weitere Aufgaben mit Lösungen