Hefteintrag
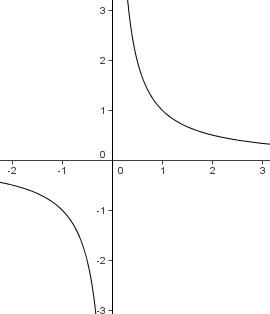
1. Den Graphen der Funktion f mit y = 1/x bezeichnet man als Hyperbel oder Ur-Hyperbel.
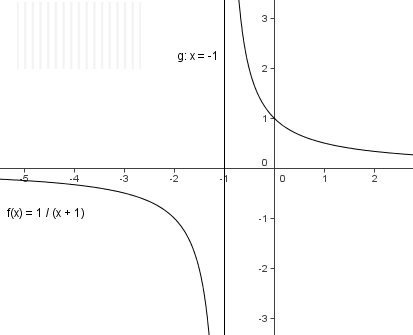
2. Der Graph der Funktion f mit y = 1/(x+a) ist ebenfalls eine Hyperbel. Er entspricht dem Graph der Ur-Hyperbel, verschoben um den Wert a nach links.
Beachte: Für x=-a ist die Funktion nicht definiert.
In diesem Applet kannst du a mit dem Schieberegler variieren.
Für die x-Werte größer als -a gilt, je mehr sich x an -a annähert, desto größer wird y.
Für die x-Werte kleiner als -a gilt, je mehr sich x an -a annähert, desto kleiner wird y.
Die Gerade x = -a ist vertikale Asymptote.
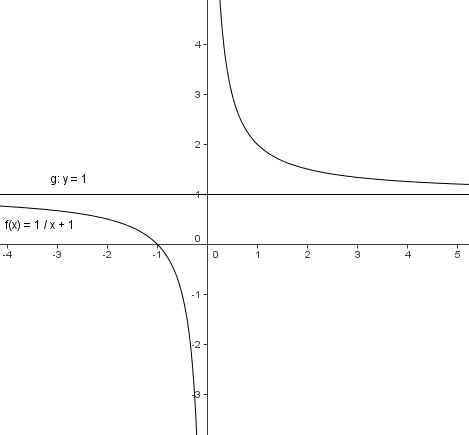
3. Der Graph der Funktion y = 1/x +b ist ebenfalls eine Hyperbel. Er entspricht dem Graph der Orthogonal-Hyperbel, verschoben um den Wert b nach oben.
Beachte: Für x=0 ist die Funktion nicht definiert.
In diesem Applet kannst du b mit dem Schieberegler variieren.
Für die x-Werte sehr viel größer als 0 gilt, je größer x wird, desto mehr nähert sich y an b an.
Für die x-Werte sehr viel kleiner als 0 gilt, je kleiner x wird, desto mehr nähert sich y an b an.
Die Gerade y = b ist horizontale Asymptote.
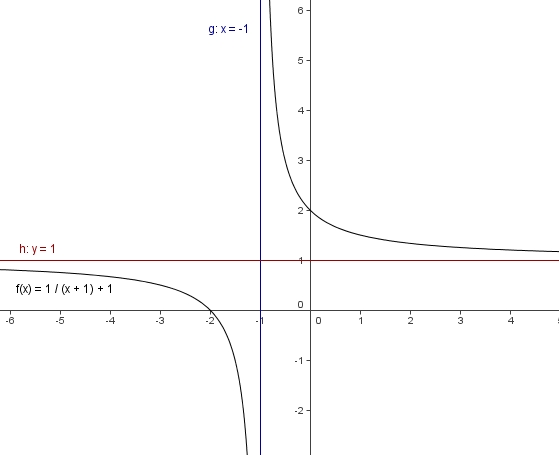
4. Der Graph der Funktion f mit y = c/(x+a) +b ist ebenfalls eine Hyperbel.
Er entspricht dem Graphen der Ur-Hyperbel, verschoben
um den Wert a nach links und um den Wert b nach oben.
Für x = -a ist die Funktion nicht definiert.
In diesem Applet kannst du die drei Parameter a, b, c mit Schiebereglern variieren.
Der Graph hat die Gerade x = -a als vertikale Asymptote und y = b als horizontale Asymptote.