2m14.2020

Hier noch die Überlegungen zur Aufgabe 136/15c:

Nachtrag zur Aufgabe 136/15c

Es wäre schön, wenn Sie als "Hausaufgabe" S. 144/1 machen. Setzen Sie hierzu, wie wir es im Unterricht gemacht haben, die Geradengleichung in die Normalenform der Ebenengleichung ein und betrachten das Ergebnis.

[Lösung anzeigen][Lösung ausblenden]

Bemerkung: Ich verwende statt griechischer Buchstaben deutsche, da sich das leichter schreiben lässt.

1a) 2(-2+k) + (2-k) + 2(1+4k)-5 = 0 hat Lösung k = 5/9, also schneidet die Gerade g die Ebene E im Punkt 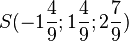$S(-1\frac{4}{9}; 1\frac{4}{9}; 2 \frac{7}{9})$
b) 6(6k)-2(-4+12k)-3(4k)-8=0 hat Lösung 0 = 0. Die Gleichung ist allgemeingültig, also liegt die Gerade g in der Ebene E.
c) 4-2k+2=0 hat als Lösung k = 3, also schneidet die Gerade g die Ebene E im Punkt S(-1;-2;4).
d) Die Normalform lässt sich schreiben als -2x₁+x₂+x₃+6=0.
Die Gleichung -2(1+k) - 2k + 1-k + 6=0 hat die Lösung k = 1, also schneidet die Gerade g die Ebene E im Punkt S(2;-2;0).
e) Normalform: x₁+2x₃=0
Die Gleichung 2-2k +2(3+k)=0 lässt sich umformen zu 6 = 0, also führt zu einer falschen Aussage. Damit ist die Gerade g (echt) parallel zur Ebene E. f) Normalform: x₂+3x₃-5=0
3+k + 3(5+4k)-5 = 0 hat die Lösung k = -1, also schneidet die Gerade g die Ebene E im Punkt S(-1;2,1).

Sie erhalten den Schnittpunkt S, indem Sie den Wert von k in die Geradengleichung einsetzen.