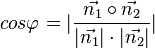Winkelberechnungen
Aus RSG-Wiki
Version vom 22. März 2020, 12:34 Uhr von Karlhaberl (Diskussion | Beiträge)
|
Merke:
Der (spitze oder rechte) Schnittwinkel |
|
Merke:
Der (spitze oder rechte) Schnittwinkel |
|
Merke:
Der (spitze oder rechte) Schnittwinkel |
Zurück zu Abstands-_und_Winkelbestimmungen

 zweier Geraden
zweier Geraden 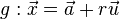 und
und 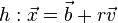 ist gegeben durch
ist gegeben durch 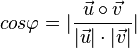
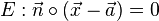 ist gegeben durch
ist gegeben durch 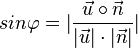
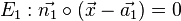 und einer Ebene
und einer Ebene 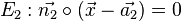 ist gegeben durch
ist gegeben durch