M8 - Beispiele weiterer gebrochen-rationaler Funktionen
Du hast schon verschiedene Graphen gebrochen-rationaler Funktionen gesehen. Hier sollen nun weitere Beispiele gezeigt werden um zu sehen, was alles vorkommen kann.
Du hast für die in direkte Proportionalität 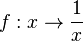 gesehen, dass bei x = 0 eine Defintionslücke ist und der Graph dort eine senkrechte Asymptote x = 0 hat.
gesehen, dass bei x = 0 eine Defintionslücke ist und der Graph dort eine senkrechte Asymptote x = 0 hat.
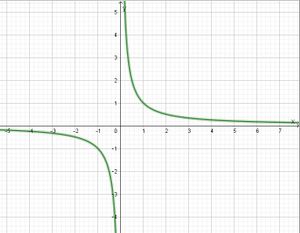
Bei Annäherung von x an 0 gehen die y-Werte, wenn x negativ ist nach 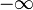 und wenn x positiv ist nach
und wenn x positiv ist nach  und nähern sich der Asympote immer mehr an.
und nähern sich der Asympote immer mehr an.
Anders schaut es schon bei dieser Funktion 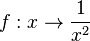 aus. Diese Funktion hat auch bei x = 0 eine Definitionslücke und der Graph eine senkrechte Asymptote x = 0.
aus. Diese Funktion hat auch bei x = 0 eine Definitionslücke und der Graph eine senkrechte Asymptote x = 0.
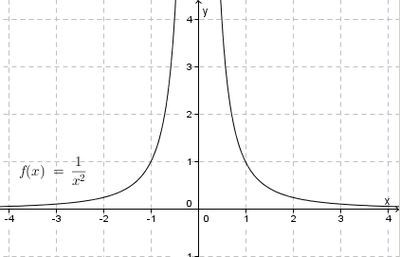
Bei Annäherung von x an 0 , egal ob mit negativen oder positiven x, gehen die y-Werte an 0 nach  und nähern sich der Asymptote immer mehr an.
und nähern sich der Asymptote immer mehr an.
Die Funktion Funktion 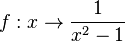 hat wegen x2-1=(x+1)(x-1) zwei Definitionslücken bei x = -1 und x = 1. Ihr Graph schaut dann so aus.
hat wegen x2-1=(x+1)(x-1) zwei Definitionslücken bei x = -1 und x = 1. Ihr Graph schaut dann so aus.
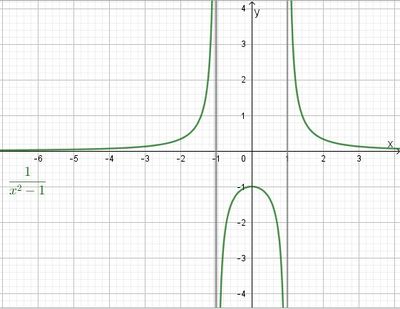
Der Graph hat zwei Asymptoten bei den Definitionslücken x = -1 und x = 1 und nähert sich an diese jeweils unterschiedlich an. Die Funktionswerte gehen je nach Annäherung an die Definitionslücken nach 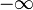 oder
oder  .
.
30px Merke
Hat der Graph einer gebrochen-rationalen Funktion bei einer Definitionslücke x = a eine senkrechte Asymptote x = a, dann heißt die Definitionslücke Polstelle. |
Du hast auch schon gesehen (Aufgabe S. 117/11), dass gebrochen-rationale Funktionen keine senkrechten Asymptoten haben.
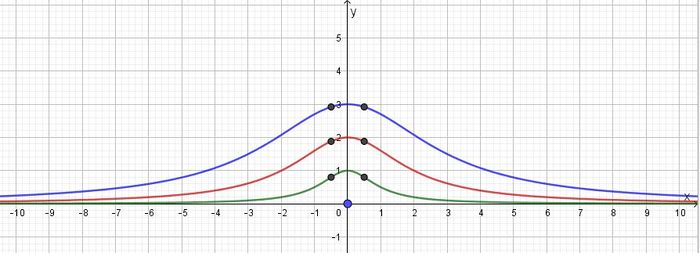
Hier sind die Graphen achsensymmetrisch zur y-Achse.
Beachte, dass eine Postelle als Definitionslücke mit Asymptote hauptsächlich eine Nullstelle des Nenners ist.
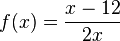 |
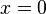
|
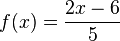 |
keine Polstelle |
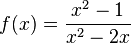 |
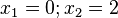
|
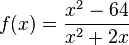 |
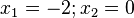
|
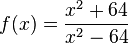 |
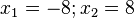
|
Für 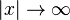 treten waagrechte Asymptoten auf, z.B. die x-Achse oder eine Parallele zu ihr.Es gibt aber auch schräge Asymptoten.
treten waagrechte Asymptoten auf, z.B. die x-Achse oder eine Parallele zu ihr.Es gibt aber auch schräge Asymptoten.
Im folgenden Beispiel stehen in Zähler und Nenner Terme mit x, der Zählerterm ist eine x-Potenz. Man kann den Exponenten der Zählerpotenz ändern und man sieht die Auswirkungen auf den Graphen und die Asymptoten.
Die senkrechte Asymptote ist für alle Fälle bei x = 1 und ändert sich nicht.
Ist n = 1 oder n = 2 (die x-Potenz im Zähler ist x oder x2 ist kleiner als die Zählerpotenz x3 im Nenner), dann die x-Achse y = 0 für  waagrechte Asymptote.
waagrechte Asymptote.
Bei n = 3 (man hat hier x3 als höchste x-Potenz in Zähler und Nenner, also gleiche x-Potenz) ist die waagrechte Asymptote in y-Richtung verschoben und y = 0,5 istfür  waagrechte Asymptote.
waagrechte Asymptote.
 sogar schräg und die Gerade hat die Gleichung y = 0,5x + 1,5.
sogar schräg und die Gerade hat die Gleichung y = 0,5x + 1,5.
30px Merke
Für |
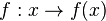 richtig zu!
richtig zu!
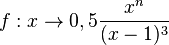 für n = 1, 2, 3, 4. In dem Applet kann man mit dem Schieberegler den Exponenten von x im Zählerpolynom ändern.
für n = 1, 2, 3, 4. In dem Applet kann man mit dem Schieberegler den Exponenten von x im Zählerpolynom ändern.

