M8 Bruchgleichungen

  Aufgabe 1

Bevor du Bruchgleichungen kennenlernst, wiederhole das Lösen von Gleichungen mit Äquivalenzumformungen aus der 7. Klasse.
Bearbeite dazu in Mathegym den Arbeitsauftrag Wiederholung 7. Klasse: Lösen von Gleichungen

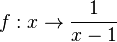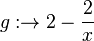Zu Beginn der Bruchterme haben wir gebrochen-rationale Funktionen betrachtet. Im folgenden Bild sind die zwei Graphen der Funktionen $f:x\rightarrow \frac{1}{x-1}$ und $g: \rightarrow 2 - \frac{2}{x}$ gezeichnet.

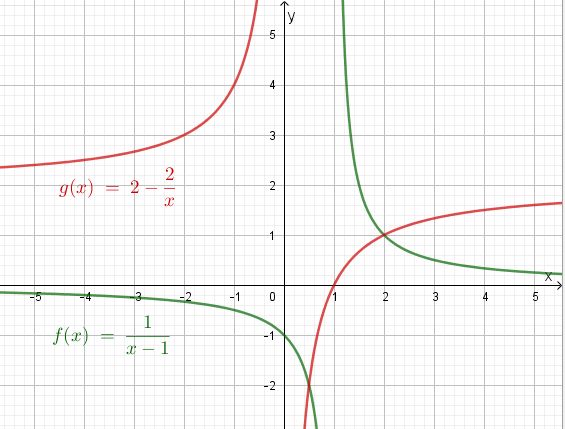
Die zwei Graphen schneidet sich in zwei Punkten. Die Koordinaten des rechten Schnittpunkts S kann man ablesen. Es ist S(2;1). Die Koordinaten des zweiten Schnittpunkte T kann man nicht so leicht ablesen. Es könnte T(0,5;-2) sein. Aber ist man sich sicher?
Eine Überprüfung wäre hier durch Einsetzen von x im Funktionsterm möglich. Wenn der richtige y-Wert herauskommt, dann hat man die richtigen Koordinaten des Schnittpunkts. Es ist f(2)= 1 = g(2) und f(0,5) = -1 = g(0,5). Also richtig abgelesen!

Bei der Behandlung linearer Funktionen hatten wir auch schon den Schnittpunkt zweier Geraden. Wir haben die Geraden gezeichnet und aus dem Diagramm den Schnittpunkt abgelesen. Wir haben aber auch den Schnittpunkt berechnet, indem wir die zwei Geradengleichungen gleichgesetzt haben. Dieses Rechenverfahren wollen wir nun hier bei unseren zwei Hyperbeln auch anwenden. Im Schnittpunkt haben beide Funktionsgraphen den gleichen x- und den gleichen y-Wert. Wir setzen die beiden Funktionsterme (gleiche y-Werte) gleich 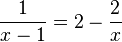$\frac{1}{x-1} = 2 - \frac{2}{x}$ . Nun muss man diese Gleichung lösen und erhält die x-Koordinate des Schnittpunktes.

Merke: Eine Bruchgleichung ist eine Gleichung mit mindestens einem Bruch, der die Unbekannte im Nenner enthält.

Wie löst man nun die Bruchgleichung 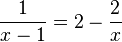$\frac{1}{x-1} = 2 - \frac{2}{x}$? Wie löst man überhaupt eine Bruchgleichung?

Wir haben jetzt gelernt wie man mit Bruchtermen rechnet. Dies wenden wir nun mit dem Lösen von Gleichungen zusammen an. Zuerst schreiben wir den Term auf der rechten Seite als Bruch. Es ist 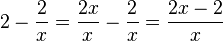$2 - \frac{2}{x}=\frac{2x}{x}- \frac{2}{x}=\frac{2x-2}{x}$ .

Dann hat man die Glelichung 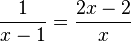$\frac{1}{x-1} = \frac{2x-2}{x}$.
Immer wenn man Bruchterme hat muss man sich zuerst überlegen, welche Zahlen man für x einsetzen darf. Das liefert die Definitionsmenge der Bruchgleichung. Hier stehen die Terme x-1 und x in den Nennern. Nenner dürfen nicht Null werden, also darf man x = 1 und x = 0 nicht einsetzen. Die Definitionsmenge hier ist also D = Q\{0;1}.

Nun kann man daran gehen die Gleichung 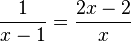$\frac{1}{x-1} = \frac{2x-2}{x}$ zu lösen. Was bei Bruchgleichungen immer stört sind die Brüche. Mulitpliziert man die Gleichung mit dem Term (x-1)x, dann erhält man
$\frac{1}{x-1} = \frac{2x-2}{x} \quad \mid \cdot (x-1)x$
$\frac{(x-1)x}{x-1} = \frac{(2x-2)(x-1)x}{x}$
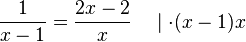
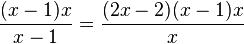
Im Zähler und Nenner des Bruchs auf der linken Seite der Gleichung steht der gleiche Faktor x-1 und auf der rechten Seite der
Gleichung der gleiche Faktor x. Gleiche Faktoren kann man kürzen!
$x = (2x-2)(x-1)$
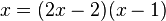
Dies ist eine Gleichung, die man nun lösen muss.
$x = 2x^2 - 2x - 2x +2$
$x = 2x^2 - 4x + 2 \quad \mid -x$ $0 = 2x^2 - 5x + 2 \quad \mid :2$ $0 = x^2 - 2,5x + 1 \quad \mid :2$

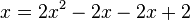
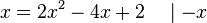
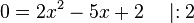
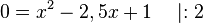
Diese Art von Gleichung lernst du in der 9. Klasse zu lösen. Aber wir haben ja schon zwei Lösungen x = 2 und x = 0,5.
Setzt man für x diese Werte ein, dann ist die Gleichung richtig.
Man kann den Term 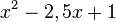$x^2 - 2,5x + 1$ auch als Produkt schreiben: $x^2 - 2,5x + 1=(x-2)(x-0,5)$.
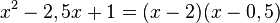(Multipliziere das Produkt 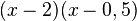$(x-2)(x-0,5)$aus, dann erhältst du den Term auf der linken Seite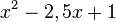 $x^2 - 2,5x + 1$
Ein Produkt hat den Wert 0, wenn ein Faktor den Wert 0 annimmt. Der erste Faktor x-2 hat für x = 2 den Wert 0,
der zweite Faktor x-0,5 hat für x = 0,5 den Wert 0. Das sind unsere beiden Lösungen vom Ablesen am Graphen.

Zuletzt gibt man noch die Lösungsmenge an: L = {0,5; 2}