Asymptoten bei rationalen Funktionen: Unterschied zwischen den Versionen
| Zeile 28: | Zeile 28: | ||
<ggb_applet width="710" height="656" version="4.0" ggbBase64="UEsDBBQACAAIADtGPEEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAA7RjxBAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbNVZW5PbthV+dn7FGXYm420sCeBNkiM5k6RN66mTdGbdTicP6UAkJCFLggwBaqmdPPan9Gf0zX+sBwBJUXtR9uK4rsZaAMTBOTjfuVJefNHkGex4pUQhlx4dEw+4TIpUyM3Sq/V6NPO+ePXJYsOLDV9VDNZFlTO99EJDKdKlRxjhZBrwEZ/F4Shk82A0S0kwIvMwiQKyDlfh1ANolHgpi+9YzlXJEn6ebHnO3hQJ01bwVuvy5WRyeXk57kSNi2oz2WxW40alHuA1pVp67eQlsjs6dBlYcp8QOvnHt28c+5GQSjOZcA+MCrV49cmzxaWQaXEJlyLV26U3pTMPtlxstqjTdBZ6MDFEJQJS8kSLHVd4dLC0Ouu89CwZk2b/mZtB1qvjQSp2IuUV4jMOoohGgU+CIPRjamQUleBSt7S0lTnpuC12gl86tmZmJeIhXRTZihmO8Msv4BOfwAszUDf4OMSx2yLuGQnc4LshdEPkaEJ3PHSkoaMJHU0YeLATSqwyvvTWLFOIoJDrCq3Xr5XeZ9zep31w0J6+QJ2UuELigKCbOMjxOSEvzDfGb2g2JsdK0oFUXdUPFNqJnNIHiPSfpGjQyfSj6KZMP7pDzfiEUKf3ffSk0UBPFGX/2e8NicEpNa9LdOunCYzDD6LiYtKFyqKNDlBbQ9t6j+a5MvESzCGaG7enEGFsxFP08gjoHIepDxgNQCMII1zSGcRmnEIwxY0QApiBoaMB2OCIZvgnnFpmMUTIzDydYkwCRUEhRAFQG1MhYCSBjUuMUT9AiiiCCA8Z8dQ3LIIYwhhXwQxCvKMJySlFwgAP4hrF+xBQCMxhOgU/htjwo6EJ9Xhmro4sfYgJxNQwxKjGiHbRjPQzCIw2cQuXkGWtjyBK8rSb6qLsbYHUmI8OWc/lp6Ok+GyRsRXPsE6cG0sC7FhmIsIKWhdSQ2dE3z3bVKzcikSdc63xlIKf2I69YZo33yC16mRb2qSQ6q9Vob8usjqXCiApMtLfucjoYO73t8ZFMNgIhxvRYCMezKe3yi1wB2rFUX5RqY6cpelrQ3FIDYjk9zLbf1VxdlEW4liNxcSWnAWvk0ykgsm/o7MaKQYXOFQgcqhAsT/rLlJU6fleoQdD8wOvCswx89l4Gs77D1bVvduJQn/sD3awpKmEmdAL5+P58INZat9uRWRMhp/WcnzX24c1vFd9U4l0OH+tviqytAfC6v41K3Vd2cYBE2NlNPpSbjJu/cOmWqzKycWqaM6dYwSO19t9iSvi5K82FnOo2qS6aceVGy2NuVhPRSwNsRSk8zSR9vt07lsKO67caKnQdd3VWkVppyUlnRihXIvjHcWM9ful13hQS6HfuBXGj0guWlWpO/Bdna/4wX0MwR+E60hcq3Usht4qZv9exCwm17xwccErybPW6dHgdVErF8ODeEh5InJcuo0WOGaM+je8k3ua8k3FW3qW2dbNwWp3ydCfbzy2rL6pivy13L1Fj7l2gcWku+VCJZUojV/CCgvFBT/4XioUwzqTDs+ZKEU0ElNPEBBt0ML4rfW2qGx3hmkHRxOcGc+xFwNtnVDWOa9E0oMvbZuHl6rbe/dWM8BDsfoJ8+E1g9mFpcHtO9wUWFZumWkOaeuMbM+rI2gst2+LtBPcis1MVwm5cGUyZ43tDdlKYabU2FajKeShrXYXazMN9iSmaW9MDJjJ3oSgna1FMwAUMRJX6BPsSJlDuGjM4hfYqiob07qNXjv5s0hTLvvbMoneY22Aiax0Dlty7ny9P1ii8jZrDOzemuWGgcwteqSZ93hLRNTlFBIOjEFOGuP79VpxbfAbhdTCF8xvtZV/u/bG2PfTv40XZW3Vmsra7gpl9y74GIvwn6U7olwKEXmZiUToB6C+uol618Fdhx3DMBUOAVMpW+o/mUbgn/Quy+C70o0oOW2Y3wh50gVJizw5CXzwMOB582Dgk/cDvP9/B/yIjKP/KfLp+0E+eH/IH3JRMLVYTX97s1gzHNkFJ2TYeJL4Q5tpha99nMneEF1uuVa2B/p8mMI9tI9vQYuik4U9webZGMg++1Lt81IXmsP63X8qkLDEN1cmr/AtgcvHAOJ/VIC44hnFs6cA4j8JkOCjAqT1kNmTAAnuBqQpKwxBc7hV5C1vNFoBN5bepz/Xhf78PNkKjq8RHBvyCq7qHN79S2KrKSHlCj79HSWf/7EpC4kcOd4BWTUgcvjh3b+3eOClY2IFH8OPr/faOxZ7GuOBIe4D8n0LVPfCcWujDLbRclaYxb8O37qFbv28OUPkMS/C76H58bk8gwk8b2AE9OzH5/6Z+yHlGJB1Le1ryUHhR3WxtmQ8ApGD2xkGqO8oPpmXbk3l4alUfgo6wLzeYsevYeefwWfoU58BdcX+12Dj94bt9pK8+UjboIfXzvvnvs0HyHr371tcvMXk9qxHbsl6rM16QiVbDn+pq90g/4V35r/J8OcA+7tc+19Mr/4LUEsHCFCwFBE6BwAA/xoAAFBLAQIUABQACAAIADtGPEFFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAO0Y8QVCwFBE6BwAA/xoAAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAADSBwAAAAA=" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | <ggb_applet width="710" height="656" version="4.0" ggbBase64="UEsDBBQACAAIADtGPEEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAA7RjxBAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbNVZW5PbthV+dn7FGXYm420sCeBNkiM5k6RN66mTdGbdTicP6UAkJCFLggwBaqmdPPan9Gf0zX+sBwBJUXtR9uK4rsZaAMTBOTjfuVJefNHkGex4pUQhlx4dEw+4TIpUyM3Sq/V6NPO+ePXJYsOLDV9VDNZFlTO99EJDKdKlRxjhZBrwEZ/F4Shk82A0S0kwIvMwiQKyDlfh1ANolHgpi+9YzlXJEn6ebHnO3hQJ01bwVuvy5WRyeXk57kSNi2oz2WxW40alHuA1pVp67eQlsjs6dBlYcp8QOvnHt28c+5GQSjOZcA+MCrV49cmzxaWQaXEJlyLV26U3pTMPtlxstqjTdBZ6MDFEJQJS8kSLHVd4dLC0Ouu89CwZk2b/mZtB1qvjQSp2IuUV4jMOoohGgU+CIPRjamQUleBSt7S0lTnpuC12gl86tmZmJeIhXRTZihmO8Msv4BOfwAszUDf4OMSx2yLuGQnc4LshdEPkaEJ3PHSkoaMJHU0YeLATSqwyvvTWLFOIoJDrCq3Xr5XeZ9zep31w0J6+QJ2UuELigKCbOMjxOSEvzDfGb2g2JsdK0oFUXdUPFNqJnNIHiPSfpGjQyfSj6KZMP7pDzfiEUKf3ffSk0UBPFGX/2e8NicEpNa9LdOunCYzDD6LiYtKFyqKNDlBbQ9t6j+a5MvESzCGaG7enEGFsxFP08gjoHIepDxgNQCMII1zSGcRmnEIwxY0QApiBoaMB2OCIZvgnnFpmMUTIzDydYkwCRUEhRAFQG1MhYCSBjUuMUT9AiiiCCA8Z8dQ3LIIYwhhXwQxCvKMJySlFwgAP4hrF+xBQCMxhOgU/htjwo6EJ9Xhmro4sfYgJxNQwxKjGiHbRjPQzCIw2cQuXkGWtjyBK8rSb6qLsbYHUmI8OWc/lp6Ok+GyRsRXPsE6cG0sC7FhmIsIKWhdSQ2dE3z3bVKzcikSdc63xlIKf2I69YZo33yC16mRb2qSQ6q9Vob8usjqXCiApMtLfucjoYO73t8ZFMNgIhxvRYCMezKe3yi1wB2rFUX5RqY6cpelrQ3FIDYjk9zLbf1VxdlEW4liNxcSWnAWvk0ykgsm/o7MaKQYXOFQgcqhAsT/rLlJU6fleoQdD8wOvCswx89l4Gs77D1bVvduJQn/sD3awpKmEmdAL5+P58INZat9uRWRMhp/WcnzX24c1vFd9U4l0OH+tviqytAfC6v41K3Vd2cYBE2NlNPpSbjJu/cOmWqzKycWqaM6dYwSO19t9iSvi5K82FnOo2qS6aceVGy2NuVhPRSwNsRSk8zSR9vt07lsKO67caKnQdd3VWkVppyUlnRihXIvjHcWM9ful13hQS6HfuBXGj0guWlWpO/Bdna/4wX0MwR+E60hcq3Usht4qZv9exCwm17xwccErybPW6dHgdVErF8ODeEh5InJcuo0WOGaM+je8k3ua8k3FW3qW2dbNwWp3ydCfbzy2rL6pivy13L1Fj7l2gcWku+VCJZUojV/CCgvFBT/4XioUwzqTDs+ZKEU0ElNPEBBt0ML4rfW2qGx3hmkHRxOcGc+xFwNtnVDWOa9E0oMvbZuHl6rbe/dWM8BDsfoJ8+E1g9mFpcHtO9wUWFZumWkOaeuMbM+rI2gst2+LtBPcis1MVwm5cGUyZ43tDdlKYabU2FajKeShrXYXazMN9iSmaW9MDJjJ3oSgna1FMwAUMRJX6BPsSJlDuGjM4hfYqiob07qNXjv5s0hTLvvbMoneY22Aiax0Dlty7ny9P1ii8jZrDOzemuWGgcwteqSZ93hLRNTlFBIOjEFOGuP79VpxbfAbhdTCF8xvtZV/u/bG2PfTv40XZW3Vmsra7gpl9y74GIvwn6U7olwKEXmZiUToB6C+uol618Fdhx3DMBUOAVMpW+o/mUbgn/Quy+C70o0oOW2Y3wh50gVJizw5CXzwMOB582Dgk/cDvP9/B/yIjKP/KfLp+0E+eH/IH3JRMLVYTX97s1gzHNkFJ2TYeJL4Q5tpha99nMneEF1uuVa2B/p8mMI9tI9vQYuik4U9webZGMg++1Lt81IXmsP63X8qkLDEN1cmr/AtgcvHAOJ/VIC44hnFs6cA4j8JkOCjAqT1kNmTAAnuBqQpKwxBc7hV5C1vNFoBN5bepz/Xhf78PNkKjq8RHBvyCq7qHN79S2KrKSHlCj79HSWf/7EpC4kcOd4BWTUgcvjh3b+3eOClY2IFH8OPr/faOxZ7GuOBIe4D8n0LVPfCcWujDLbRclaYxb8O37qFbv28OUPkMS/C76H58bk8gwk8b2AE9OzH5/6Z+yHlGJB1Le1ryUHhR3WxtmQ8ApGD2xkGqO8oPpmXbk3l4alUfgo6wLzeYsevYeefwWfoU58BdcX+12Dj94bt9pK8+UjboIfXzvvnvs0HyHr371tcvMXk9qxHbsl6rM16QiVbDn+pq90g/4V35r/J8OcA+7tc+19Mr/4LUEsHCFCwFBE6BwAA/xoAAFBLAQIUABQACAAIADtGPEFFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAO0Y8QVCwFBE6BwAA/xoAAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAADSBwAAAAA=" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
</center> | </center> | ||
| − | + | Da das Nennerpolynom Grad 2 hat sieht man für n = 4 die asymptotische Parabel, an die sich der Graph für <math> x \rightarrow \pm \infty</math> annähert. | |
<br><br> | <br><br> | ||
[http://www.chemgapedia.de/vsengine/vlu/vsc/de/ma/1/mc/ma_04/ma_04_02/ma_04_02_02.vlu/Page/vsc/de/ma/1/mc/ma_04/ma_04_02/ma_04_02_19.vscml.html Hier] sind die Überlegungen nochmals zusammengefasst. | [http://www.chemgapedia.de/vsengine/vlu/vsc/de/ma/1/mc/ma_04/ma_04_02/ma_04_02_02.vlu/Page/vsc/de/ma/1/mc/ma_04/ma_04_02/ma_04_02_19.vscml.html Hier] sind die Überlegungen nochmals zusammengefasst. | ||
Version vom 28. September 2012, 18:58 Uhr
|
Eine Gerade |
Anschaulich kann man es sich so vorstellen, dass der Graph und die Gerade für 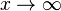 beliebig nahe kommen ohne sich zu schneiden.
beliebig nahe kommen ohne sich zu schneiden.
30px Aufgabe
Wir betrachten im folgenden Applet die Funktion Was kannst du über die Asymptoten mit Änderung des Zählerexponenten aussagen? |
|
Bezeichnet z den Grad den Zählerpolynoms und n den Grad des Nennerpolynoms, dann gilt:
|
Im folgenden Applet ist eine ähnliche Funktionenschar wie oben dargestellt: 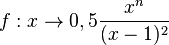 für n = 1, 2, 3, 4. Der Grad des Nennerpolynoms ist diesmal 2.
für n = 1, 2, 3, 4. Der Grad des Nennerpolynoms ist diesmal 2.
n lässt sich wieder mit dem Schieberegler variieren.
Da das Nennerpolynom Grad 2 hat sieht man für n = 4 die asymptotische Parabel, an die sich der Graph für  annähert.
annähert.
Hier sind die Überlegungen nochmals zusammengefasst.
Zusammenfassung mit Beispielen:
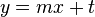 heißt Asymptote für
heißt Asymptote für  , wenn
, wenn ![\lim_{x \to \infty}[f(x)-(mx+t)]=0](/images/math/f/5/c/f5cd18892342f11d8223eaae23b54111.png) ist.
ist.
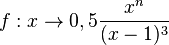 für n = 1, 2, 3, 4. In dem Applet kann man mit dem Schieberegler den Exponenten von x im Zählerpolynom ändern.
für n = 1, 2, 3, 4. In dem Applet kann man mit dem Schieberegler den Exponenten von x im Zählerpolynom ändern.
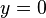 Asymptote.
Asymptote.
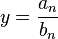 Asymptote.
Asymptote.
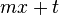 und einen Restbruch umwandeln. Der lineare Term
und einen Restbruch umwandeln. Der lineare Term 
