Aufgaben zur Lagebezeihung zweier Ebenen: Unterschied zwischen den Versionen

Aus RSG-Wiki
Wechseln zu: Navigation, Suche
Zeile 84: Zeile 84:
 
(II) -1 + 2k = 3 - r - 2s<br>
 
(II) -1 + 2k = 3 - r - 2s<br>
 
(III) 2k = -2 + r + s<br>
 
(III) 2k = -2 + r + s<br>
−
 
+
Zusammenfassen liefert:<br>
−
 
+
(I)    k - 2s = -4<br>
−
 
+
(II)  2k + r + 2s = 4<br>
−
   
+
(III) 2k - r - s = -2<br>
−
}}
+
Gleichung (I) liefert k = 2s -4. Also setzt man 2s - 4 für k in die Gleichungen (II) und (III) und erhält<br>
 +
(II) 6s + r = 12<br>
 +
(III)3s - r = 6<br>
 +
Addiert man beide Gleichungen ergibt sich 9s = 18 und s = 2. Dies führt zu r = 0 und ebenso k = 0. Einsetzen in die Geradengleichung oder Ebenengleichung ergibt den angegebenen Schnittpunkt.}}
  
 
146/13
 
146/13

Version vom 20. März 2020, 15:46 Uhr

Wenn Sie DreiDGeo heruntergeladen haben, können Sie die Ebenen dort schön darstellen und Ihr Ergebnis überprüfen.

S. 146/7
Bei dieser Aufgabe ist sind die Ebenen, diesmal E2 in Normalenform und Ebene E1 in Parameterform gegeben. Also kann man relativ einfach die "Parameterform in die Normalenform" einsetzen. Man setzt die Koordinaten des Ortsvektors 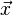\vec{x} eines Punktes X der Ebene E1 in die Normalenform der Ebene E2.

Da griechische Buchstaben sich hier nur sehr umständlich schreiben lassen, verwende ich k und m.

a) -4(1+m) + 3(2+k-2m) - (-1+3k+2m) = 3
-4 - 4m +6 +3k -6m + 1 - 3k - 2m = 3
3 - 12m = 3
m = 0
Nun ersetzt man m in die Parametergleichung der Ebene E1 durch 0:
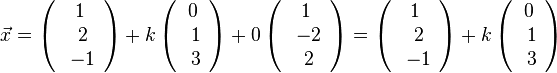\vec{x} = \left( \begin{array}{c} 1 \\\ 2 \\\ -1 \end{array}\right) + k \left( \begin{array}{c} 0 \\\ 1 \\\ 3 \end{array}\right) + 0 \left( \begin{array}{c} 1 \\\ -2 \\\ 2 \end{array}\right) = \left( \begin{array}{c} 1 \\\ 2 \\\ -1 \end{array}\right) + k \left( \begin{array}{c} 0 \\\ 1 \\\ 3 \end{array}\right) ist die Gleichung der Schnittgeraden.


b) 1+m + 2(-1+3k+2m) = 5
1 + m - 2 + 6k + 4m = 5
5m + 6k = 6
k = 1 - 5/6 m
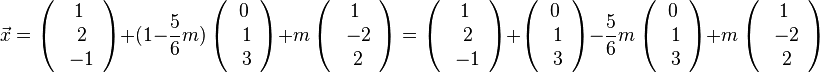
\vec{x} = \left( \begin{array}{c} 1 \\\ 2 \\\ -1 \end{array}\right) + (1 - \frac{5}{6}m) \left( \begin{array}{c} 0 \\\ 1 \\\ 3 \end{array}\right) + m \left( \begin{array}{c} 1 \\\ -2 \\\ 2 \end{array}\right) = \left( \begin{array}{c} 1 \\\ 2 \\\ -1 \end{array}\right) + \left( \begin{array}{c} 0 \\\ 1 \\\ 3 \end{array}\right) - \frac{5}{6}m \left( \begin{array}{c} 0 \\\ 1 \\\ 3 \end{array}\right) + m \left( \begin{array}{c} 1 \\\ -2 \\\ 2 \end{array}\right)
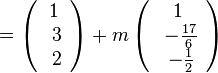
= \left( \begin{array}{c} 1 \\\ 3 \\\ 2 \end{array}\right) + m \left( \begin{array}{c} 1 \\\ -\frac{17}{6} \\\ -\frac{1}{2} \end{array}\right)


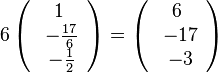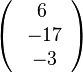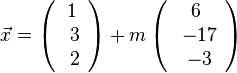Da der Richtungsvektor durch Multiplikation nur die Länge ändert, nicht aber die Richtung , hier z.B. 6 \left( \begin{array}{c} 1 \\\ -\frac{17}{6} \\\ -\frac{1}{2} \end{array}\right) = \left( \begin{array}{c} 6 \\\ -17 \\\ -3 \end{array}\right) könnte man hier auch als Richtungsvektor der Schnittgeraden \left( \begin{array}{c} 6 \\\ -17 \\\ -3 \end{array}\right) und die Schnittgerade ist dann \vec{x} = \left( \begin{array}{c} 1 \\\ 3 \\\ 2 \end{array}\right) + m \left( \begin{array}{c} 6 \\\ -17 \\\ -3 \end{array}\right) .
So wird es in DreiDGeo auch angezeigt.


d) Die Normalform lässt sich umformen in -4x1 +3x2 +x3 - 6 = 0. Vorgehen wie in a) und b) liefert 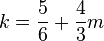k = \frac{5}{6} + \frac{4}{3} m . Setzt man dies in die Parameterform der Ebene E1 ein so ergibt sich als Schnittgerade g: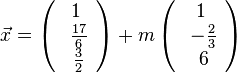 \vec{x} = \left( \begin{array}{c} 1 \\\ \frac{17}{6} \\\ \frac{3}{2} \end{array}\right) + m \left( \begin{array}{c} 1 \\\ -\frac{2}{3} \\\ 6 \end{array}\right)


e) die Normalform lässt sich schreiben als 8x1 + 3x2 - x3 =0.
Einsetzen der Koordinaten der Parameterform liefert 4 = 0, was als falsche Aussage liefert, dass die beiden Ebenen E1 und E2 echt parallel sind.


g) Einsetzen der Koordinaten der Parametergleichung in die Normalenform 8(1+m) + 3(2+k-2m) - (-1+3k+2m) -15 = 0. Vereinfachen der Gleichung liefert 0 = 0, also eine allgemeingültige Gleichung, was bedeutet, dass die beiden Ebenen E1 und E2 identisch sind.

Aufgabe 146/8

E1 ist die x1x2-Ebene.
E2 ist die x2x3-Ebene.
E3 ist die x1x3-Ebene.
E4 ist eine Parallelebene zur x1x3-Ebene bei x2=1.
E5 ist eine Parallelebene zur x1x2-Ebene bei x3=1.
E6 ist eine Parallelebene zur x2x3-Ebene bei x1=1.

Die E1-Ebene schneidet Ebene E2. Die Schnittgerade ist die x2-Achse.
Die E1-Ebene schneidet Ebene E3. Die Schnittgerade ist die x1-Achse.
Die E1-Ebene schneidet Ebene E4. Die Schnittgerade ist eine Parallel zur x1-Achse bei x2=1.
Die E1-Ebene ist echt parallel zur Ebene E5. Die E1-Ebene schneidet Ebene E6. Die Schnittgerade ist eine Parallel zur x2-Achse bei x1=1.

....

Man kann diese Aufgabe auch gut mit DreiDGeo lösen!

146/9

Die Schnittgerade ist g: 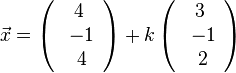\vec{x} = \left( \begin{array}{c} 4 \\\ -1 \\\ 4 \end{array}\right) + k \left( \begin{array}{c} 3 \\\ -1 \\\ 2 \end{array}\right) und die Parallele zu ihr durch P(1;-2;1) ist p: 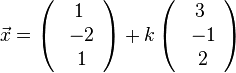\vec{x} = \left( \begin{array}{c} 1 \\\ -2 \\\ 1 \end{array}\right) + k \left( \begin{array}{c} 3 \\\ -1 \\\ 2 \end{array}\right). Die Parallele muss ja einen kollinearen Richtungsvektor haben, also kann man auch gleich den Richtungsvektor von g nehmen. Als Stützvektor nimmt man den Ortsvektor von P.

146/10

Die Ebene E ist in Normalenform x1 - x2 + x3 - 2 = 0 gegeben.
Der Vektor 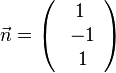\vec{n} = \left( \begin{array}{c} 1 \\\ -1 \\\ 1 \end{array}\right) ist Normalenvektor der Ebene E. Eine Parallelebene E* der Ebene E hat den gleichen Normalenvektor (oder einen zu \vec{n} kollinearen Vektor).
Die Konstante in der Normalenform ergibt sich als Skalarprodukt des Normalenvektor mit dem Stützvektor. Also rechnet man für die Ebene E* das Skalarprodukt 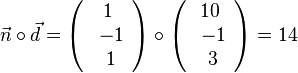\vec{n}\circ \vec{d}= \left( \begin{array}{c} 1 \\\ -1 \\\ 1 \end{array}\right) \circ \left( \begin{array}{c} 10 \\\ -1 \\\ 3 \end{array}\right) = 14. Die Normalenform der Ebenengleichung für E* ist
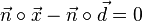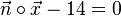\vec{n}\circ \vec{x} - \vec{n}\circ \vec{d} = 0 oder \vec{n}\circ \vec{x} - 14 = 0 oder x1 - x2 + x3 - 14 = 0.

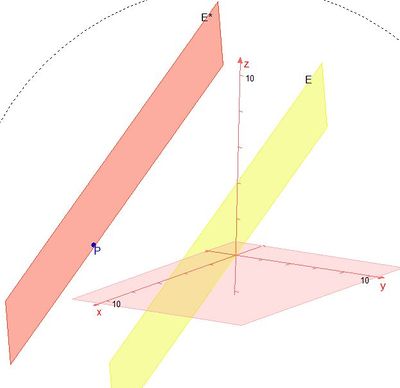
Lagebeziehung von Ebenen

146/11

In beiden Fällen ergibt sich als Schnittpunkt S(3;-1;0).
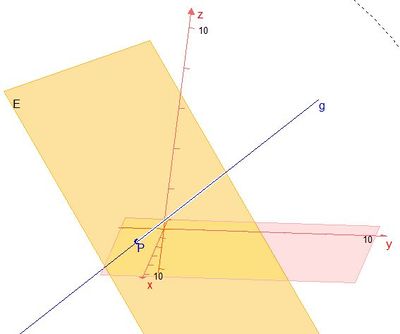
Gerade und Ebene
Nun doch die Lösung:
a) Der Vektor 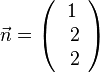\vec{n} = \left( \begin{array}{c} 1 \\\ 2 \\\ 2 \end{array}\right) ist Normalenvektor der Ebene. Als Normalenform der Ebenengleichung erhält man x1 + 2x2 + 2x3 -1 = 0. Setzt man die Koordinaten der Geradengleichung ein, erhält man r = 0 und auch den genannten Punkt S (ist hier der Stützpunkt der Gerade g).
b) Schwieriger wird es bei dieser Aufgabe: Man sucht einen Punkt X, der sowohl auf der Geraden g, also auch in der Ebene E liegt. Man setzt die beiden Vektordarstellungen von Gerade und Ebene gleich, da X sowohl ein Punkt von g als auch von E ist.
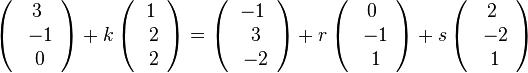
\left( \begin{array}{c} 3 \\\ -1 \\\ 0 \end{array}\right)+k \left( \begin{array}{c} 1 \\\ 2 \\\ 2 \end{array}\right) = \left( \begin{array}{c} -1 \\\ 3 \\\ -2 \end{array}\right) + r \left( \begin{array}{c} 0 \\\ -1 \\\ 1 \end{array}\right) + s \left( \begin{array}{c} 2 \\\ -2 \\\ 1 \end{array}\right)
Man hat also ein Gleichungssystem von 3 Gleichungen mit 3 Unbekannten k, r und s.
(I) 3 + k = -1 + 2s
(II) -1 + 2k = 3 - r - 2s
(III) 2k = -2 + r + s
Zusammenfassen liefert:
(I) k - 2s = -4
(II) 2k + r + 2s = 4
(III) 2k - r - s = -2
Gleichung (I) liefert k = 2s -4. Also setzt man 2s - 4 für k in die Gleichungen (II) und (III) und erhält
(II) 6s + r = 12
(III)3s - r = 6

Addiert man beide Gleichungen ergibt sich 9s = 18 und s = 2. Dies führt zu r = 0 und ebenso k = 0. Einsetzen in die Geradengleichung oder Ebenengleichung ergibt den angegebenen Schnittpunkt.

146/13

Der Vektor 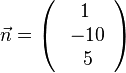\vec{n} = \left( \begin{array}{c} 1 \\\ -10 \\\ 5 \end{array}\right) ist Normalenvektor der Ebene E. Richtungsvektoren der Ebene müssen senkrecht zum Normalenvektor stehen. Das Skalarprodukt aus Richtungsvektor und Normalenvektor ist dann 0. Man überprüft also die entsprechenden Skalarprodukte.
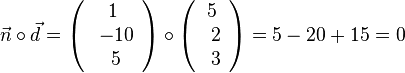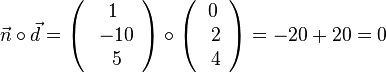a) \vec{n}\circ \vec{d}= \left( \begin{array}{c} 1 \\\ -10 \\\ 5 \end{array}\right) \circ \left( \begin{array}{c} 5 \\\ 2 \\\ 3 \end{array}\right) = 5 - 20 + 15 = 0 und \vec{n}\circ \vec{d}= \left( \begin{array}{c} 1 \\\ -10 \\\ 5 \end{array}\right) \circ \left( \begin{array}{c} 0 \\\ 2 \\\ 4 \end{array}\right) = - 20 + 20 = 0. Also sind die beiden Vektoren mögliche Richtungsvektoren der Ebene E.

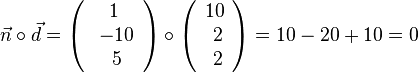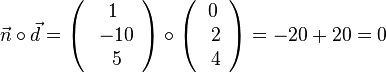b) \vec{n}\circ \vec{d}= \left( \begin{array}{c} 1 \\\ -10 \\\ 5 \end{array}\right) \circ \left( \begin{array}{c} 10 \\\ 2 \\\ 2 \end{array}\right) = 10 - 20 + 10 = 0 und \vec{n}\circ \vec{d}= \left( \begin{array}{c} 1 \\\ -10 \\\ 5 \end{array}\right) \circ \left( \begin{array}{c} 0 \\\ 2 \\\ 4 \end{array}\right) = - 20 + 20 = 0. Also sind die beiden Vektoren mögliche Richtungsvektoren der Ebene E.

c) 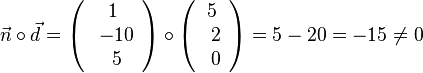\vec{n}\circ \vec{d}= \left( \begin{array}{c} 1 \\\ -10 \\\ 5 \end{array}\right) \circ \left( \begin{array}{c} 5 \\\ 2 \\\ 0 \end{array}\right) = 5 - 20 = -15 \neq 0. Dieser Vektor ist nicht geeignet, also auch das Paar nicht. Der zweite Vektor würde gehen, da 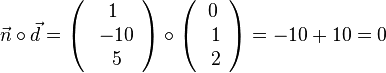\vec{n}\circ \vec{d}= \left( \begin{array}{c} 1 \\\ -10 \\\ 5 \end{array}\right) \circ \left( \begin{array}{c} 0 \\\ 1 \\\ 2 \end{array}\right) = - 10 + 10 = 0 ist.

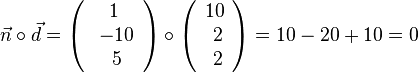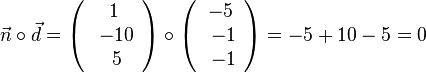d) \vec{n}\circ \vec{d}= \left( \begin{array}{c} 1 \\\ -10 \\\ 5 \end{array}\right) \circ \left( \begin{array}{c} 10 \\\ 2 \\\ 2 \end{array}\right) = 10 - 20 + 10 = 0 und \vec{n}\circ \vec{d}= \left( \begin{array}{c} 1 \\\ -10 \\\ 5 \end{array}\right) \circ \left( \begin{array}{c} -5 \\\ -1 \\\ -1 \end{array}\right) = -5 + 10 -5 = 0. Also sind die beiden Vektoren mögliche Richtungsvektoren der Ebene E.

Was macht man, wenn beide Ebenen in Parameterform dargestellt sind?
Man kann die beiden Gleichungen gleichsetzen und erhält 3 Gleichungen mit 4 Unbekannten.

Oder was macht man, wenn beide Ebenen in Normalenform angegeben sind?

S. 146/14

Die Normalenformen der Ebene E1 ist 3x1 + x2 - 2x3 - 6 = 0 und die Normalenform der Ebene E2 ist x1 - x2 -3 x3 - 12 = 0. Verwandelt man eine Normalenform in eine Parameterform, dann kann man für die Lagebeziehung wieder das uns bekannte Verfahren anwenden.
In dieser Aufgabe geht es darum die beiden Normalenformen der Ebenengleichungen in Punkt-Richtungsformen (Parameterformen) überzuführen.

Am Beispiel der Ebene E2 wird ein Weg dargestellt.
Man setzt x2 = r und x3 = 2. Dann hat man folgende Gleichung x1 - r - 3x - 12 = 0.
Diese Gleichung löst man nach x1 auf, es ist dann x1 = 12 + r + 3s.
Jetzt geht es relativ einfach weiter. Jeder Punkt X der Ebene E2 hat einen Ortsvektor 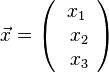\vec{x} = \left( \begin{array}{c} x_1 \\\ x_2 \\\ x_3 \end{array}\right). Setzt man nun für x1 die den gerade erhaltenen Term 12 + r + 3s ein, für x2 = r und für x3 = s, so ist
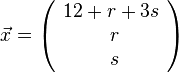\vec{x} = \left( \begin{array}{c} 12+r+3s \\\ r \\\ s \end{array}\right). Disen Vektor kann man nun aufspalten in Vektoren ohne r und s und Vektoren, bei denen man r bzw. s aus dem Vektor herausziehen kann (S-Multiplikation!). Es ist dann

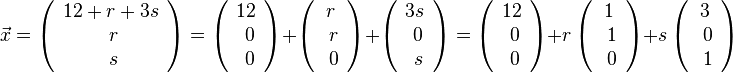\vec{x} = \left( \begin{array}{c} 12+r+3s \\\ r \\\ s \end{array}\right) = \left( \begin{array}{c} 12 \\\ 0 \\\ 0 \end{array}\right) + \left( \begin{array}{c} r \\\ r \\\ 0 \end{array}\right) + \left( \begin{array}{c} 3s \\\ 0 \\\ s \end{array}\right) = \left( \begin{array}{c} 12 \\\ 0 \\\ 0 \end{array}\right) + r \left( \begin{array}{c} 1 \\\ 1 \\\ 0 \end{array}\right) + s\left( \begin{array}{c} 3 \\\ 0 \\\ 1 \end{array}\right) . Und das ist eine Ebenengleichung in Parameterform mit Stützvektor und zwei Richtungsvektoren.
Von „http://rsg.zum.de/index.php?title=Aufgaben_zur_Lagebezeihung_zweier_Ebenen&oldid=8672“