Aufgaben zur Lagebezeihung zweier Ebenen

Wenn Sie DreiDGeo heruntergeladen haben, können Sie die Ebenen dort schön darstellen und Ihr Ergebnis überprüfen.

S. 146 / 7
Bei dieser Aufgabe ist sind die Ebenen, diesmal E₂ in Normalenform und Ebene E₁ in Parameterform gegeben. Also kann man relativ einfach die "Parameterform in die Normalenform" einsetzen. Man setzt die Koordinaten des Ortsvektors 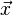$\vec{x}$ eines Punktes X der Ebene E₁ in die Normalenform der Ebene E₂.

[Lösung anzeigen][Lösung ausblenden]

Da griechische Buchstaben sich hier nur sehr umständlich schreiben lassen, verwende ich k und m.

a) -4(1+m) + 3(2+k-2m) - (-1+3k+2m) = 3
-4 - 4m +6 +3k -6m + 1 - 3k - 2m = 3
3 - 12m = 3
m = 0
Nun ersetzt man m in die Parametergleichung der Ebene E₁ durch 0:
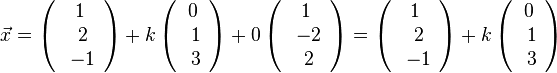$\vec{x} = \left( \begin{array}{c} 1 \\\ 2 \\\ -1 \end{array}\right) + k \left( \begin{array}{c} 0 \\\ 1 \\\ 3 \end{array}\right) + 0 \left( \begin{array}{c} 1 \\\ -2 \\\ 2 \end{array}\right) = \left( \begin{array}{c} 1 \\\ 2 \\\ -1 \end{array}\right) + k \left( \begin{array}{c} 0 \\\ 1 \\\ 3 \end{array}\right)$ ist die Gleichung der Schnittgeraden.

b) 1+m + 2(-1+3k+2m) = 5
1 + m - 2 + 6k + 4m = 5
5m + 6k = 6
k = 1 - 5/6 m
$\vec{x} = \left( \begin{array}{c} 1 \\\ 2 \\\ -1 \end{array}\right) + (1 - \frac{5}{6}m) \left( \begin{array}{c} 0 \\\ 1 \\\ 3 \end{array}\right) + m \left( \begin{array}{c} 1 \\\ -2 \\\ 2 \end{array}\right) = \left( \begin{array}{c} 1 \\\ 2 \\\ -1 \end{array}\right) + \left( \begin{array}{c} 0 \\\ 1 \\\ 3 \end{array}\right) - \frac{5}{6}m \left( \begin{array}{c} 0 \\\ 1 \\\ 3 \end{array}\right) + m \left( \begin{array}{c} 1 \\\ -2 \\\ 2 \end{array}\right)$
$= \left( \begin{array}{c} 1 \\\ 3 \\\ 2 \end{array}\right) + m \left( \begin{array}{c} 1 \\\ -\frac{17}{6} \\\ -\frac{1}{2} \end{array}\right)$

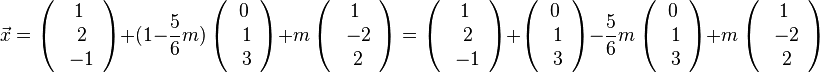
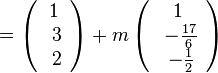
Da der Richtungsvektor durch Multiplikation nur die Länge ändert, nicht aber die Richtung , hier z.B. 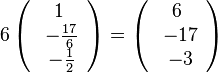$6 \left( \begin{array}{c} 1 \\\ -\frac{17}{6} \\\ -\frac{1}{2} \end{array}\right) = \left( \begin{array}{c} 6 \\\ -17 \\\ -3 \end{array}\right)$ könnte man hier auch als Richtungsvektor der Schnittgeraden 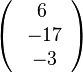$\left( \begin{array}{c} 6 \\\ -17 \\\ -3 \end{array}\right)$ und die Schnittgerade ist dann $\vec{x} = \left( \begin{array}{c} 1 \\\ 3 \\\ 2 \end{array}\right) + m \left( \begin{array}{c} 6 \\\ -17 \\\ -3 \end{array}\right)$ .
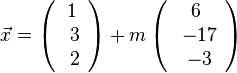So wird es in DreiDGeo auch angezeigt.

d) Die Normalform lässt sich umformen in -4x₁ +3x₂ +x₃ - 6 = 0. Vorgehen wie in a) und b) liefert 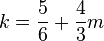$k = \frac{5}{6} + \frac{4}{3} m$. Setzt man dies in die Parameterform der Ebene E₁ ein so ergibt sich als Schnittgerade g: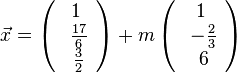 $\vec{x} = \left( \begin{array}{c} 1 \\\ \frac{17}{6} \\\ \frac{3}{2} \end{array}\right) + m \left( \begin{array}{c} 1 \\\ -\frac{2}{3} \\\ 6 \end{array}\right)$

e) die Normalform lässt sich schreiben als 8x₁ + 3x₂ - x₃ =0.
Einsetzen der Koordinaten der Parameterform liefert 4 = 0, was als falsche Aussage liefert, dass die beiden Ebenen E₁ und E₂ echt parallel sind.

g) Einsetzen der Koordinaten der Parametergleichung in die Normalenform 8(1+m) + 3(2+k-2m) - (-1+3k+2m) -15 = 0. Vereinfachen der Gleichung liefert 0 = 0, also eine allgemeingültige Gleichung, was bedeutet, dass die beiden Ebenen E₁ und E₂ identisch sind.