Gebrochen-rationale Funktionen 8: Unterschied zwischen den Versionen
| Zeile 2: | Zeile 2: | ||
Eine Funktion f ist eine gebrochen-rationale Funktion, wenn ihr Funktionsterm einen Bruch enthält, in dessen Nenner die Variable x vorkommt.<br> | Eine Funktion f ist eine gebrochen-rationale Funktion, wenn ihr Funktionsterm einen Bruch enthält, in dessen Nenner die Variable x vorkommt.<br> | ||
Der Wert für x für den der Nenner Null wird heißt Definitionslücke.}} | Der Wert für x für den der Nenner Null wird heißt Definitionslücke.}} | ||
| + | |||
| + | Der Graph der indirekten Proportionalität <math>f: x \rightarrow \frac{1}{x}</math> für <math> x \not= 0 </math> ist eine Hyperbel.<br> | ||
| + | Mehr zu Hyperbeln lernst du in diesem Lernpfad kennen | ||
| + | [[Datei:lernpfad.jpg]] [http://www.matheprisma.uni-wuppertal.de/Module/Hyperbel/index.htm Hyperbeln] | ||
Im folgenden Applet ist zuerst die Funktion <math> f: x\rightarrow \frac{1}{x}</math> dargestellt. Es gibt zwei Schieberegler. Damit kannst du den Wert der Parameter <math>b</math> und <math>c</math> verändern. <math>b</math> ist ein Parameter, der im Nenner der Funktion als <math> x-b</math> hinzugefügt wird, <math>c</math> wird beim Funktionsterm addiert, so dass du die Funktion <math> f: x\rightarrow \frac{1}{x-b}+c</math> betrachten kannst. | Im folgenden Applet ist zuerst die Funktion <math> f: x\rightarrow \frac{1}{x}</math> dargestellt. Es gibt zwei Schieberegler. Damit kannst du den Wert der Parameter <math>b</math> und <math>c</math> verändern. <math>b</math> ist ein Parameter, der im Nenner der Funktion als <math> x-b</math> hinzugefügt wird, <math>c</math> wird beim Funktionsterm addiert, so dass du die Funktion <math> f: x\rightarrow \frac{1}{x-b}+c</math> betrachten kannst. | ||
| Zeile 24: | Zeile 28: | ||
2. Die x-Achse wird um c in y-Richtung verschoben. Die Gerade y = c ist, da sich die Hyperbeläste für große x an sie annähern, Asymptote für <math> x \rightarrow \pm\infty</math>.<br> | 2. Die x-Achse wird um c in y-Richtung verschoben. Die Gerade y = c ist, da sich die Hyperbeläste für große x an sie annähern, Asymptote für <math> x \rightarrow \pm\infty</math>.<br> | ||
Die Gerade y = c ist waagrechte Asymptote.<br>}} | Die Gerade y = c ist waagrechte Asymptote.<br>}} | ||
| + | |||
| + | {{Merke| | ||
| + | Eine Gerade heißt Asymptote zur Funktion f, wenn der Graph der Funktion f der Geraden beliebig nahe kommt ohne sie zu schneiden.}} | ||
| + | |||
| + | {{Aufgabe-M|1= | ||
| + | Im folgenden Applet betrachten wir die Funktion <math>f:x\rightarrow 0,5\frac{x^n}{(x-1)^3}</math> für n = 1, 2, 3, 4. In dem Applet kann man mit dem Schieberegler den Exponenten von x im Zählerpolynom ändern. | ||
| + | |||
| + | Was kannst du über die Asymptoten mit Änderung des Zählerexponenten aussagen? | ||
| + | }} | ||
| + | <center> | ||
| + | <ggb_applet width="736" height="487" version="4.0" ggbBase64="UEsDBBQACAAIANU+PEEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACADVPjxBAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbNVZ2Y7jthJ9nnxFQQGCmWBsiyIl2RN7gux3gMkC9CQI8pCAlmibaYlSJMotN/J4PyWfcd/mx26RlGS5N/SsSYx2kxSLtZxaWOpeftrmGexFVctCrTwy9T0QKilSqbYrr9Gbydz79OkHy60otmJdcdgUVc71ymOGUqYrz+e+8GMqJmIesQnjCzqZpz6d+AuWhNTfsDWLPYC2lk9U8R3PRV3yRJwlO5Hz50XCtRW807p8MptdXFxMe1HTotrOttv1tK1TD1BNVa+8bvIE2Z0cuqCWPPB9Mvv52+eO/USqWnOVCA+MCY18+sGD5YVUaXEBFzLVu5UXM+bBTsjtDm2KSOjBzBCVCEgpEi33osajo6W1WeelZ8m4MvsP3AyywRwPUrmXqagQn2nAWBTQKAwXhC7iOcooKimU7mhJJ3PWc1vupbhwbM3MSkQtdVFka244wp9/QuAHPjw2A3FDgEMUuS3fPfOpGwI3MDeEjoa548yRMkfDHA2jHuxlLdeZWHkbntWIoFSbCr03rGt9yITVp3twtJ48RptqeYnE1McwcZDjc99/bL4RfpnZmJ0aSUZSddW8otBeZEyj+4sM3shQ2ssk8+C6zCC8xczoDqHO7vvYScIRtCjK/tjvNYn0LjOvSnTrNxMYsfdi4nLWp8qyyw6od4a2ix4t8trkC11AuDBhTyDE3IhijPIQyAKHOADMBiAhsBCXZA6RGWOgMW4woDAHQ0co2OQI5/iLxZZZBCEyM09jzEkgKIhBSIHYnGKAmQQ2LzFHA4oUYQghHjLiSWBY0AhYhCs6B4Y6mpSMCRJSPIhrFB8AJUDNYRJDEEFk+BFmUj2aG9WRZQCRDxExDDGrMaNdNiP9HKixJurgkqps9AlESZ72U12Ugy+QGuvRseq5+nRSFB8sM74WGd4TZ8aTAHuemYywgjaF0tA7MXDPthUvdzKpz4TWeKqG3/meP+datF8jdd3LtrRJoeofqkJ/UWRNrmqApMj8QeciI6N5MGiNCzraYOONcLQRjebxjXIL3IGmFii/qOqenKfpM0NxLA2I5PcqO3xeCX5eFvLUjOXMXjlL0SSZTCVXP2GwGikGFxhuIFOu+huIhYtekaJKzw41RjC0v4iqwFK1YNOYLYYP3qqHbmce4yVz3ImQY51wk3tsMV2MP5iXh24r9Kf++NO5SewHB/FWDLZvK5mO58/qz4ssHZCwxn/BS91UtnPAylgZkz5T20zYALG1Fq/l5HxdtGcuMqjj9eJQ4sp38tdbCzpgYQhCvCu33bh2o6Uxig1UvqXxLYXfh5pMh32yCCyFHddutFQYu061zlDSW0n8XoysXY/jnSSNDfyV13rQKKmfuxUmkEzOO1OJO/Bdk6/FMX4MwZfStSSu1zoVQ24Uc3grYpazK2G4PBeVElkX9ejwpmhql8SjhEhFInNcuo0OOG6c+iPq5J6mYluJjp5ntndzsNpdfxzQ1x5bVl9XRf5M7V9gxFxRYDnrtVzWSSVLE5ewxpviXBxjL5U1x4smHZ8zaYpoJOZCQUC0QQsTuNG7orLtGdYdHE12ZiLHZgy0DULV5KKSyQC+sn0eKtV0eg9eM8BDsf4dC+IVh9mFpcHtW8IUeFbuuOkOSReM/CCqE2gst2+LtBfcic1MWwm5dPdkzlvbHPJ1jaVSY1+NrlDHvtop1pUabEpM196aHDCTg0lBO9vIdgQoYiQvMSb4iTHHdNFYxs+xV61tTusue+3kPzJNhRq05Qqjx/oAK1npArYUwsX6cLBE423VGPm9c8s1BxktBqS59/qeCImrKT4bOcO/0xnfbza10Aa/CSMWPrq40VfBzdYbZ9/P/i5fauurzlXWd5coewjB1/GI+EO5I7UrITIvM5lIfQ31tqyQn1G+A3ODb4ataREeto9gBf40hI+h/fWhegQzeNjCBMijXx/SR657OPXaplE2Fb0js9fxHAnpLVl0X8cZBojlJLozyW4Elt0F7D0Ddn3d7L77vWo3VrBUuuAxXUZH/Y1pon4jtwW1BeiVoHlHQev39aULWv/OmKWvFrMYhjfH7O3AJ28H+OBfB/wE8/RvRT59O8jTt4f8sRrQ2GIVv3u3WDec+IW8f7+s8R1Z8GMR7ovJlRZnZMD7aXJGDlm46KU0uNEnHZ/+NaLvW0YhhK8gxleW+rP6kJe60AI2L/9XgcJbi0Bh2iczDYCrS3zvEup1UAv+SajNFw61kL0b1OgbQUX/UVDNHVTxO4KK3Q7VtY7qhWg16bqqj/5oCv3JWbKTAt/lBL4VVXDZ5PDyvwoDVkEqavjoQ+J/8lVbFgo5CtQBWbUgc/jl5V87PPDEMfGu918aJXmnYu9Gf+Si+8B/36uuf+u78W0FbLcbWP/Mo6vwzcavdPaPK93/CZ7+H1BLBwjtuV/UAgcAAMQYAABQSwECFAAUAAgACADVPjxBRczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIANU+PEHtuV/UAgcAAMQYAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAmgcAAAAA" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | </center> | ||
| + | |||
| + | {{Lösung versteckt| 1= | ||
| + | Bezeichnet z den Grad den Zählerpolynoms und n den Grad des Nennerpolynoms, dann gilt:<br> | ||
| + | * Ist z < n, dann ist für <math>x \rightarrow \pm \infty</math> die x-Achse <math> y = 0</math> Asymptote. | ||
| + | * Ist z = n und ist <math>a_n </math> der Koeffizient von <math>x^n</math> im Zählerpolynom und <math>b_n</math> der Koeffizient von <math>x^n</math> im Nennerpolynom, dann ist für <math>x \rightarrow \pm \infty</math> die Gerade <math>y = \frac{a_n}{b_n}</math> Asymptote. | ||
| + | * Ist z = n+1,dann gibt es eine schräge Asymptote. | ||
| + | |||
| + | }} | ||
Version vom 20. April 2016, 07:27 Uhr
|
Eine Funktion f ist eine gebrochen-rationale Funktion, wenn ihr Funktionsterm einen Bruch enthält, in dessen Nenner die Variable x vorkommt. |
Der Graph der indirekten Proportionalität 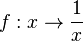 für
für 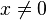 ist eine Hyperbel.
ist eine Hyperbel.
Mehr zu Hyperbeln lernst du in diesem Lernpfad kennen
![]() Hyperbeln
Hyperbeln
Im folgenden Applet ist zuerst die Funktion 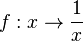 dargestellt. Es gibt zwei Schieberegler. Damit kannst du den Wert der Parameter
dargestellt. Es gibt zwei Schieberegler. Damit kannst du den Wert der Parameter 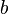 und
und  verändern.
verändern. 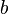 ist ein Parameter, der im Nenner der Funktion als
ist ein Parameter, der im Nenner der Funktion als 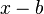 hinzugefügt wird,
hinzugefügt wird,  wird beim Funktionsterm addiert, so dass du die Funktion
wird beim Funktionsterm addiert, so dass du die Funktion 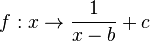 betrachten kannst.
betrachten kannst.
|
1. Ändere den Wert von b, indem du am Schieberegler für b ziehst. |
1. Die Gerade x = b ist an der Stelle der Defintionslücke x = b. Bei Veränderung von b, ändert sich die Definitionslücke, die Gerade wandert mit.
Die Gerade x = b ist eine senkrechte Asymptote.
2. Die x-Achse wird um c in y-Richtung verschoben. Die Gerade y = c ist, da sich die Hyperbeläste für große x an sie annähern, Asymptote für  .
.
|
Eine Gerade heißt Asymptote zur Funktion f, wenn der Graph der Funktion f der Geraden beliebig nahe kommt ohne sie zu schneiden. |
|
Im folgenden Applet betrachten wir die Funktion Was kannst du über die Asymptoten mit Änderung des Zählerexponenten aussagen? |
Bezeichnet z den Grad den Zählerpolynoms und n den Grad des Nennerpolynoms, dann gilt:
- Ist z < n, dann ist für
 die x-Achse
die x-Achse 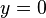 Asymptote.
Asymptote.
- Ist z = n und ist
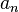 der Koeffizient von
der Koeffizient von 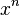 im Zählerpolynom und
im Zählerpolynom und 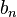 der Koeffizient von
der Koeffizient von 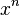 im Nennerpolynom, dann ist für
im Nennerpolynom, dann ist für  die Gerade
die Gerade 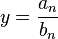 Asymptote.
Asymptote.
- Ist z = n+1,dann gibt es eine schräge Asymptote.
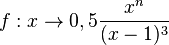 für n = 1, 2, 3, 4. In dem Applet kann man mit dem Schieberegler den Exponenten von x im Zählerpolynom ändern.
für n = 1, 2, 3, 4. In dem Applet kann man mit dem Schieberegler den Exponenten von x im Zählerpolynom ändern.

