Gebrochen-rationale Funktionen 8: Unterschied zwischen den Versionen
| Zeile 68: | Zeile 68: | ||
{{Aufgaben-blau||2=Veränderte in obigen Applet den Wert von a indem du den Schieberegler betätigst. <br> | {{Aufgaben-blau||2=Veränderte in obigen Applet den Wert von a indem du den Schieberegler betätigst. <br> | ||
| − | a) Was passiert mit dem gezeichneten Graphen?<br> | + | a) Wo hat die Funktion eine Definitionslücke? Gib die Definitionsmenge an. |
| − | + | b)Was passiert mit dem gezeichneten Graphen?<br> | |
| − | + | c) Welchen besonderen Namen hat auch dieser Graph?<br> | |
| + | d) Lies aus dem Applet die Geradengleichung der senkrechten roten Geraden ab. <br> | ||
| + | e) Was passiert mit der eingezeichneten senkrechten Asymptote. | ||
| + | f) Fasse deine Überlegungen zusammen.}} | ||
| − | + | {{Lösung versteckt|1=a) Die Funktion hat bei x = a eine Definitionslücke. D = Q\[a}. a nimmt stets den durch den Schieberegler eingestellten Wert an.<br> | |
| − | + | b)Der Graph wird für positive a nach rechts (in positive x-Richtung) verschoben. Für negative a wird er nach links (in negative x-Richtung verschoben.<br> | |
| − | {{Lösung versteckt|1=a) Der Graph wird für positive a nach rechts (in positive x-Richtung) verschoben. Für negative a wird er nach links (in negative x-Richtung verschoben.<br> | + | c) Es handelt sich auch hier um eine Hyperbel.<br> |
| − | + | d) x = a, wobei a der gerade am Schieberegler eingestellte Wert ist. <br> | |
| − | + | e) Die senkrecht Asymptote wird wie der Graph verschoben, also für a > 0 nach rechts und für a < 0 nach links. | |
| − | + | f) Die Funktion <math>f: x\rightarrow \frac{2}{x-a}, x\neq a</math> ist nicht definiert für x = a, dort hat sie eine Defintionslücke, ihre Definitionsmenge ist D = Q\{0}. Ihr Graph ist eine Hyperbel. Man erhält diese Hyperbel, indem man den Hyperbel der Funktion <math>f: x\rightarrow \frac{2}{x}, x\neq 0</math> um a in Richtung der x-Achse verschiebt.}} | |
| − | }} | + | |
Version vom 23. März 2020, 09:58 Uhr
|
Eine Funktion f ist eine gebrochen-rationale Funktion, wenn ihr Funktionsterm einen Bruch enthält, in dessen Nenner die Variable x vorkommt. |
Beispiele für Funktionsterme gebrochen-rationaler Funktionen sind 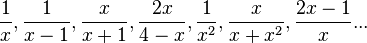 .
.
Im Nenner eines Bruches darf nie 0 stehen. Deshalb muss man diese Wert aus der Grundmenge Q (Menge der rationalen Zahlen) herausnehmen. Alle Zahlen, die man in den Term einsetzen darf stehen auch bei gebrochen-rationalen Funktionen in der Definitionsmenge D.
Um die Definitionslücke zu finden musst du den Nenner gleich 0 setzen und diese Gleichung lösen. Die erhaltenen Zahlen sind aus der Grundmenge Q zu entfernen.
 hat D = Q\{0},
hat D = Q\{0},
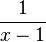 hat D = Q \{1},
hat D = Q \{1},
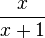 hat D = Q\{-1},
hat D = Q\{-1},
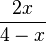 hat D = Q\{4},
hat D = Q\{4},
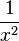 hat D = Q\{0},
hat D = Q\{0},
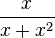 hat D = Q\{-1;1},
hat D = Q\{-1;1},
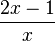 hat D = Q\{0}
hat D = Q\{0}Die Funktion der indirekten Proportionalität 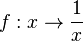 für
für 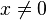 ist die einfachste gebrochen-rationale Funktion.
ist die einfachste gebrochen-rationale Funktion.
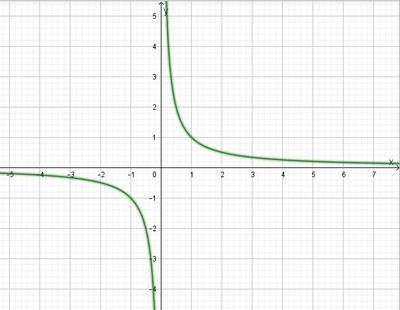
Ihr Graph ist eine Hyperbel und besteht aus zwei Hyperbelästen.
An der Stelle x = 0 ist die Funktion nicht definiert. Ihr Graph nähert sich der y-Achse (x = 0) beliebig nahe an. Die y-Achse ist eine senkrechte Asymptote. Betrachtet man die Funktion für sehr große x, d.h. 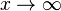 oder sehr kleine x, d.h.
oder sehr kleine x, d.h. 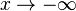 dann nähert sich der Graph beliebig nahe an die x-Achsse an. Die x-Achse ist eine waagrechte Asymptote.
dann nähert sich der Graph beliebig nahe an die x-Achsse an. Die x-Achse ist eine waagrechte Asymptote.
|
Eine Gerade heißt Asymptote zum Funktionsgraf Gf, wenn sich der Funktionsgraph beliebig nahe an die Gerade annähert ohne sie zu berühren. |
a) Hier sind viele lineare Funktionen dabei. Die musst du richtig herausfinden. Desweiteren ist Graph 2 eine Hyperbel und Graph 4 eine Parabel.
Den Geraden kannst du leicht die richtigen Funktionsgleichungen zuordnen:
Graph 1 und Gleichung II, Graph 3 und Gleichung V, Graph 5 und Gleichung I, Graph 6 und Term VI.
Die Hyperbel (Graph 2) gehört zu einer Bruchgleichung, also Gleichung IV.
Dann bleibt für die Parabel (Graph 4) nur die Gleichung III.
Im Nenner steht der Term x. Dieser nimmt für x=0 den Wert 0 an, also darf man 0 nicht in den Term  einsetzen. x=0 ist Definitionslücke und D = Q\{0}.
einsetzen. x=0 ist Definitionslücke und D = Q\{0}.
Wertetabelle:
![]()
Für x = 0 ist der Term nicht definiert, also taucht 0 auch nicht in der Wertetabelle auf. Falls du 0 in der Wertetabelle hast, dann schreibe beim zugehörigen y-Wert n.d. für nicht definiert.
Graph:
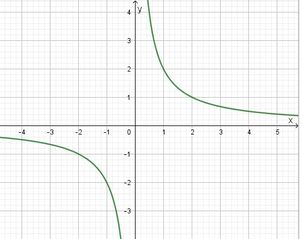
b) y = 0 (x-Achse) ist waagrechte Asymptote, x = 0 (y-Achse) ist senkrechte Asymptote. Der Graph nähert sich den Koordinatenachsen beliebig nahe an ohne sie zu erreichen.
c) In der Wertetabelle siehst du f(4) = 0,5. Wird x größer, dann werden die y-Werte kleiner. Das siehst du auch im Graph. Also für x > 4 sind die Funktionswerte f(x) kleiner 0,5.
d) yP = -0,5 und yP* 0 0,5. Die Gerade durch P und P* hat die Gleichung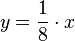 , ist eine Ursprungsgerade und geht also durch den Ursprung.
, ist eine Ursprungsgerade und geht also durch den Ursprung.Im folgenden Graph ist für a = 0 die Funktion 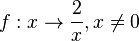 dargestellt. Diese Funktion ist dir aus der letzten Aufgabe bekannt. Ihre senkrechte Asymptote (x=0) ist rot eingezeichnet.
dargestellt. Diese Funktion ist dir aus der letzten Aufgabe bekannt. Ihre senkrechte Asymptote (x=0) ist rot eingezeichnet.
Eigentlich siehst du den Graph der Funktion 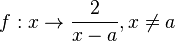 . Für a ist nur der Wert 0 eingestellt. Mit dem Schieberegler (a = 0) kannst du den Wert von a verändern.
. Für a ist nur der Wert 0 eingestellt. Mit dem Schieberegler (a = 0) kannst du den Wert von a verändern.
a) Die Funktion hat bei x = a eine Definitionslücke. D = Q\[a}. a nimmt stets den durch den Schieberegler eingestellten Wert an.
b)Der Graph wird für positive a nach rechts (in positive x-Richtung) verschoben. Für negative a wird er nach links (in negative x-Richtung verschoben.
c) Es handelt sich auch hier um eine Hyperbel.
d) x = a, wobei a der gerade am Schieberegler eingestellte Wert ist.
e) Die senkrecht Asymptote wird wie der Graph verschoben, also für a > 0 nach rechts und für a < 0 nach links.
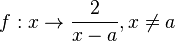 ist nicht definiert für x = a, dort hat sie eine Defintionslücke, ihre Definitionsmenge ist D = Q\{0}. Ihr Graph ist eine Hyperbel. Man erhält diese Hyperbel, indem man den Hyperbel der Funktion
ist nicht definiert für x = a, dort hat sie eine Defintionslücke, ihre Definitionsmenge ist D = Q\{0}. Ihr Graph ist eine Hyperbel. Man erhält diese Hyperbel, indem man den Hyperbel der Funktion 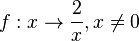 um a in Richtung der x-Achse verschiebt.
um a in Richtung der x-Achse verschiebt.
Im folgenden Applet ist zuerst die Funktion 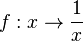 dargestellt. Es gibt zwei Schieberegler. Damit kannst du den Wert der Parameter
dargestellt. Es gibt zwei Schieberegler. Damit kannst du den Wert der Parameter 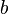 und
und  verändern.
verändern. 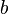 ist ein Parameter, der im Nenner der Funktion als
ist ein Parameter, der im Nenner der Funktion als 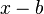 hinzugefügt wird,
hinzugefügt wird,  wird beim Funktionsterm addiert, so dass du die Funktion
wird beim Funktionsterm addiert, so dass du die Funktion 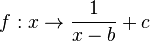 betrachten kannst.
betrachten kannst.
|
1. Ändere den Wert von b, indem du am Schieberegler für b ziehst. |
1. Die Gerade x = b ist an der Stelle der Defintionslücke x = b. Bei Veränderung von b, ändert sich die Definitionslücke, die Gerade wandert mit.
Die Gerade x = b ist eine senkrechte Asymptote.
2. Die x-Achse wird um c in y-Richtung verschoben. Die Gerade y = c ist, da sich die Hyperbeläste für große x an sie annähern, Asymptote für  .
.
Ausblick
|
Im folgenden Applet betrachten wir die Funktion Was kannst du über die Asymptoten mit Änderung des Zählerexponenten aussagen? |
Bezeichnet z den Grad den Zählerpolynoms und n den Grad des Nennerpolynoms, dann gilt:
- Ist z < n, dann ist für
 die x-Achse
die x-Achse  Asymptote.
Asymptote.
- Ist z = n und ist
 der Koeffizient von
der Koeffizient von 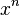 im Zählerpolynom und
im Zählerpolynom und 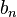 der Koeffizient von
der Koeffizient von 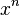 im Nennerpolynom, dann ist für
im Nennerpolynom, dann ist für  die Gerade
die Gerade 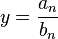 Asymptote.
Asymptote.
- Ist z = n+1,dann gibt es eine schräge Asymptote.
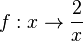 die Definitionsmenge an und zeichne mit Hilfe einer Wertetabelle den Graphen.
die Definitionsmenge an und zeichne mit Hilfe einer Wertetabelle den Graphen.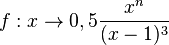 für n = 1, 2, 3, 4. In dem Applet kann man mit dem Schieberegler den Exponenten von x im Zählerpolynom ändern.
für n = 1, 2, 3, 4. In dem Applet kann man mit dem Schieberegler den Exponenten von x im Zählerpolynom ändern.

