M11 Anwendungen und Aufgaben zum Rechnen mit Vektoren: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
| + | __NOCACHE__ | ||
In den folgenden Bildern sind die Vektoren ohne Vektorpfeil angegeben. Leider macht GeoGebra das nicht. | In den folgenden Bildern sind die Vektoren ohne Vektorpfeil angegeben. Leider macht GeoGebra das nicht. | ||
| Zeile 15: | Zeile 16: | ||
Wie kommt man vom Ursprung zu M?<br> | Wie kommt man vom Ursprung zu M?<br> | ||
Man geht zuerst mit dem Vektor <math> \vec a</math> zum Punkt A und dann die Hälfte der Strecke [AB], dies geht mit dem Vekor <math>\frac{1}{2} \vec {AB} = \frac{1}{2} (\vec b -\vec a)</math>. Also insgesamt <math> \vec m = \vec a + \frac{1}{2} \vec {AB} = \vec a + \frac{1}{2} (\vec b - \vec a)=\vec a + \frac{1}{2} \vec b - \frac {1}{2} \vec a = \frac{1}{2} \vec a + \frac{1}{2} \vec b=\frac{1}{2}(\vec a +\vec b)</math>. | Man geht zuerst mit dem Vektor <math> \vec a</math> zum Punkt A und dann die Hälfte der Strecke [AB], dies geht mit dem Vekor <math>\frac{1}{2} \vec {AB} = \frac{1}{2} (\vec b -\vec a)</math>. Also insgesamt <math> \vec m = \vec a + \frac{1}{2} \vec {AB} = \vec a + \frac{1}{2} (\vec b - \vec a)=\vec a + \frac{1}{2} \vec b - \frac {1}{2} \vec a = \frac{1}{2} \vec a + \frac{1}{2} \vec b=\frac{1}{2}(\vec a +\vec b)</math>. | ||
| + | |||
| + | {{Aufgaben-blau|1|2=a) Bestimme den Mittelpunkt der Strecke mit den Endpunkten A(1,2,3) und B(6,5,4).<br> | ||
| + | b) Bestimme den Mittelpunkt der Strecke mit den Endpunkten A(-1,2,3) und B(6,0,-4). }} | ||
| + | |||
| + | {{Lösung versteckt|1=<math>\vec m = \frac{1}{2} \left [ \left ( \begin{array}{c} 1 \\\ 2 \\\ 3 \end{array}\right) + \left ( \begin{array}{c} 6 \\\ 5 \\\ 4 \end{array}\right) \right ] = \frac{1}{2} \left ( \begin{array}{c} 7 \\\ 7 \\\ 7 \end{array}\right) = \left ( \begin{array}{c} 3,5 \\\ 3,5 \\\ 3,5 \end{array}\right)</math> , also M(3,5;3,5;3,5)<br> | ||
| + | b) <math>\vec m = \frac{1}{2} \left [ \left ( \begin{array}{c} -1 \\\ 2 \\\ 3 \end{array}\right) + \left ( \begin{array}{c} 6 \\\ 0 \\\ -4 \end{array}\right) \right ] = \frac{1}{2} \left ( \begin{array}{c} 5 \\\ 2 \\\ -1 \end{array}\right) = \left ( \begin{array}{c} 2,5 \\\ 1 \\\ -0,5 \end{array}\right)</math> , also M(2,5;1;-0,5)}} | ||
| + | |||
Ein ähnliches Ergebnis erhält man für den Schwerpunkt S eines Dreiecks mit den Eckpunkten A, B, C. | Ein ähnliches Ergebnis erhält man für den Schwerpunkt S eines Dreiecks mit den Eckpunkten A, B, C. | ||
| Zeile 32: | Zeile 40: | ||
Hinweis: <math>\vec {MbS}=\frac{1}{3} \vec {MbB}</math> [https://mathepedia.de/Seitenhalbierende.html erhält man aus dem Strahlensatz!] | Hinweis: <math>\vec {MbS}=\frac{1}{3} \vec {MbB}</math> [https://mathepedia.de/Seitenhalbierende.html erhält man aus dem Strahlensatz!] | ||
| + | |||
| + | {{Aufgaben-blau|2|2=Bestimme die Koordinaten des Schwerpunkts S des Dreiecks mit den Eckpunkten A(1;2;3), B(6;5;4) und C(5;2;-1).}} | ||
| + | |||
| + | {{Lösung versteckt|1=<math>\vec s = \frac{1}{3} \left [ \left ( \begin{array}{c} 1 \\\ 2 \\\ 3 \end{array}\right) + \left ( \begin{array}{c} 6 \\\ 5 \\\ 4 \end{array}\right) + \left ( \begin{array}{c} 5 \\\ 2 \\\ -1 \end{array}\right) \right ] = \frac{1}{3} \left ( \begin{array}{c} 12 \\\ 9 \\\ 6 \end{array}\right) =\left ( \begin{array}{c} 4 \\\ 3 \\\ 2 \end{array}\right) </math>, also S(4;3;2). | ||
| + | <ggb_applet height="400" width="500" | ||
| + | filename="Schwerpunkt.ggb" /> }} | ||
Version vom 16. Januar 2021, 17:24 Uhr
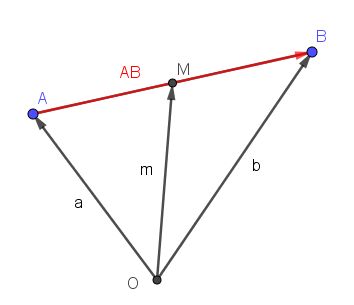
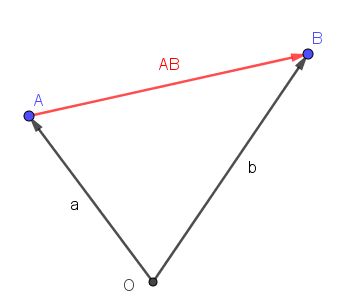
In den folgenden Bildern sind die Vektoren ohne Vektorpfeil angegeben. Leider macht GeoGebra das nicht.
Die Strecke [AB] hat einen Mittelpunkt M, dessen Ortsvektor ist 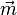 .
.
|
Merke:
Der Ortsvektor 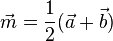 |
Wie kommt man vom Ursprung zu M?
Man geht zuerst mit dem Vektor  zum Punkt A und dann die Hälfte der Strecke [AB], dies geht mit dem Vekor
zum Punkt A und dann die Hälfte der Strecke [AB], dies geht mit dem Vekor 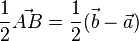 . Also insgesamt
. Also insgesamt 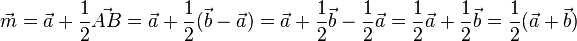 .
.
![\vec m = \frac{1}{2} \left [ \left ( \begin{array}{c} 1 \\\ 2 \\\ 3 \end{array}\right) + \left ( \begin{array}{c} 6 \\\ 5 \\\ 4 \end{array}\right) \right ] = \frac{1}{2} \left ( \begin{array}{c} 7 \\\ 7 \\\ 7 \end{array}\right) = \left ( \begin{array}{c} 3,5 \\\ 3,5 \\\ 3,5 \end{array}\right)](/images/math/a/3/c/a3c7b12f5314a6b152960748520bf2a5.png) , also M(3,5;3,5;3,5)
, also M(3,5;3,5;3,5)
![\vec m = \frac{1}{2} \left [ \left ( \begin{array}{c} -1 \\\ 2 \\\ 3 \end{array}\right) + \left ( \begin{array}{c} 6 \\\ 0 \\\ -4 \end{array}\right) \right ] = \frac{1}{2} \left ( \begin{array}{c} 5 \\\ 2 \\\ -1 \end{array}\right) = \left ( \begin{array}{c} 2,5 \\\ 1 \\\ -0,5 \end{array}\right)](/images/math/f/3/0/f306226783f22a7c9c91ce329df9c42e.png) , also M(2,5;1;-0,5)
, also M(2,5;1;-0,5)
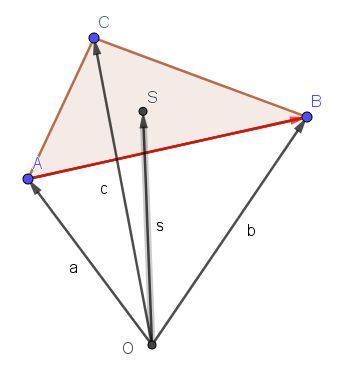
Ein ähnliches Ergebnis erhält man für den Schwerpunkt S eines Dreiecks mit den Eckpunkten A, B, C.
|
Merke:
Der Schwerpunkt S eines Dreiecks mit den Eckpunkten A, B, C und deren Ortsvektoren 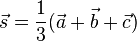 . . |
Wie kommt man vom Urpsung zu S?
Sind Ma, Mb und Mc die Mittelpunkte der Dreiecksseiten a, b, c.
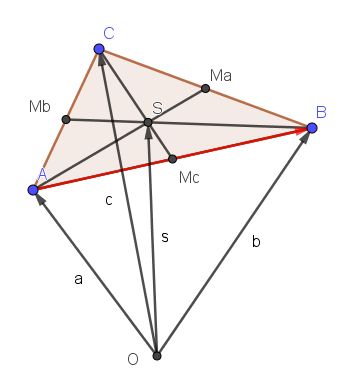
Man geht zurest mit dem Vektor  zum Punkt A, dann von A nach Mb und von Mb nach S, also
zum Punkt A, dann von A nach Mb und von Mb nach S, also
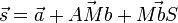
Nun ist 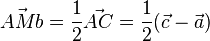 und
und ![\vec {MbS}=\frac{1}{3} \vec {MbB} = \frac{1}{3}(\vec b - \vec {Mb})=\frac{1}{3}[\vec b - \frac{1}{2}(\vec c + \vec a)]](/images/math/d/7/a/d7a561887d1ea3a28dc61125d5e3bea7.png)
Damit ist ![\vec s = \vec a+ \vec {AMb} + \vec {MbS} = \vec a + \frac{1}{2}(\vec c -\vec a) + \frac{1}{3}[\vec b - \frac{1}{2}(\vec c + \vec a)]=\vec a + \frac{1}{2} \vec c - \frac{1}{2} \vec a + \frac{1}{3} \vec b - \frac{1}{6} \vec c - \frac{1}{6}\vec a = \frac{1}{3} \vec c + \frac{1}{3} \vec b + \frac{1}{3} \vec b = \frac{1}{3} (\vec a + \vec b + \vec c)](/images/math/8/b/6/8b61a33bf8f1d7262d008bbe91303e66.png)
Hinweis: 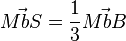 erhält man aus dem Strahlensatz!
erhält man aus dem Strahlensatz!
![\vec s = \frac{1}{3} \left [ \left ( \begin{array}{c} 1 \\\ 2 \\\ 3 \end{array}\right) + \left ( \begin{array}{c} 6 \\\ 5 \\\ 4 \end{array}\right) + \left ( \begin{array}{c} 5 \\\ 2 \\\ -1 \end{array}\right) \right ] = \frac{1}{3} \left ( \begin{array}{c} 12 \\\ 9 \\\ 6 \end{array}\right) =\left ( \begin{array}{c} 4 \\\ 3 \\\ 2 \end{array}\right)](/images/math/8/d/4/8d44ac09238feb21c794a23f61b312ff.png) , also S(4;3;2).
, also S(4;3;2).

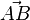 der zwei Punkte mit den Ortsvektoren
der zwei Punkte mit den Ortsvektoren 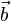 ist
ist 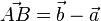 .
.
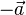 gehen und dann in Richtung
gehen und dann in Richtung 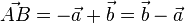 .
.
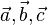 hat den Ortsvektor
hat den Ortsvektor 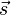 . Es ist
. Es ist 
