M11 Anwendungen und Aufgaben zum Rechnen mit Vektoren
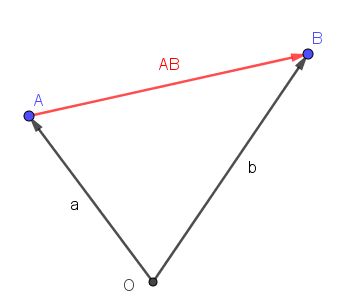
In den folgenden Bildern sind die Vektoren ohne Vektorpfeil angegeben. Leider macht GeoGebra das nicht.
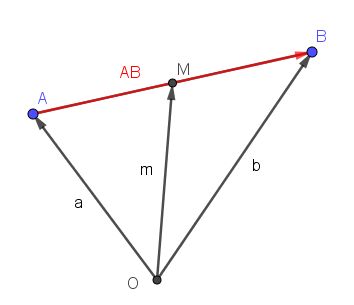
Die Strecke [AB] hat einen Mittelpunkt M, dessen Ortsvektor ist 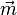 .
.
|
Merke:
Der Ortsvektor 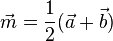 |
Wie kommt man vom Ursprung zu M?
Man geht zuerst mit dem Vektor  zum Punkt A und dann die Hälfte der Strecke [AB], dies geht mit dem Vekor
zum Punkt A und dann die Hälfte der Strecke [AB], dies geht mit dem Vekor 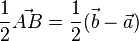 . Also insgesamt
. Also insgesamt 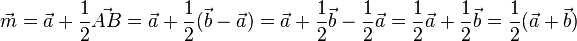 .
.
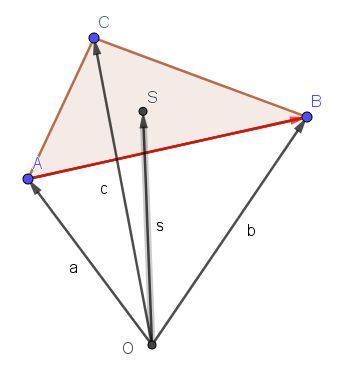
Ein ähnliches Ergebnis erhält man für den Schwerpunkt S eines Dreiecks mit den Eckpunkten A, B, C.
|
Merke:
Der Schwerpunkt S eines Dreiecks mit den Eckpunkten A, B, C und deren Ortsvektoren 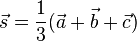 . . |
Wie kommt man vom Urpsung zu S?
Sind Ma, Mb und Mc die Mittelpunkte der Dreiecksseiten a, b, c.
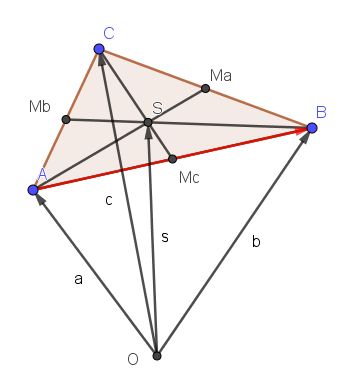
Man geht zurest mit dem Vektor  zum Punkt A, dann von A nach Mb und von Mb nach S, also
zum Punkt A, dann von A nach Mb und von Mb nach S, also
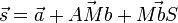
Nun ist 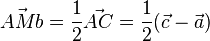 und
und ![\vec {MbS}=\frac{1}{3} \vec {MbB} = \frac{1}{3}(\vec b - \vec {Mb})=\frac{1}{3}[\vec b - \frac{1}{2}(\vec c + \vec a)]](/images/math/d/7/a/d7a561887d1ea3a28dc61125d5e3bea7.png)
Damit ist ![\vec s = \vec a+ \vec {AMb} + \vec {MbS} = \vec a + \frac{1}{2}(\vec c -\vec a) + \frac{1}{3}[\vec b - \frac{1}{2}(\vec c + \vec a)]=\vec a + \frac{1}{2} \vec c - \frac{1}{2} \vec a + \frac{1}{3} \vec b - \frac{1}{6} \vec c - \frac{1}{6}\vec a = \frac{1}{3} \vec c + \frac{1}{3} \vec b + \frac{1}{3} \vec b = \frac{1}{3} (\vec a + \vec b + \vec c)](/images/math/8/b/6/8b61a33bf8f1d7262d008bbe91303e66.png)
Hinweis: 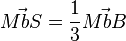 erhält man aus dem Strahlensatz!
erhält man aus dem Strahlensatz!

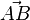 der zwei Punkte mit den Ortsvektoren
der zwei Punkte mit den Ortsvektoren 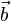 ist
ist 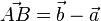 .
.
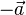 gehen und dann in Richtung
gehen und dann in Richtung 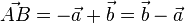 .
.
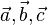 hat den Ortsvektor
hat den Ortsvektor 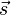 . Es ist
. Es ist 
