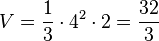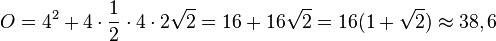M11 Aufgabe zu Vektoren
Buch S. 93 / 1 d, e
d) 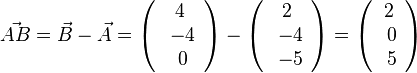
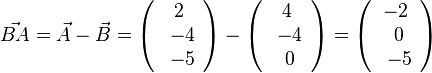
e) 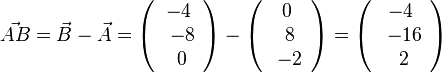
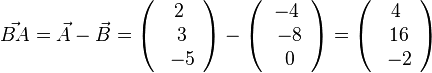
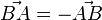
Buch S. 93 / 2
a) 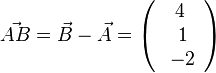 , also
, also 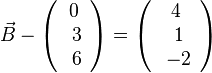 oder
oder 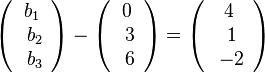 liefert
liefert 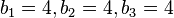 .
.
b) 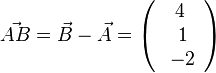 , also
, also 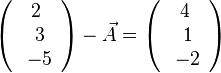 oder
oder 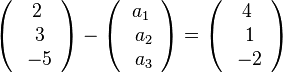 liefert
liefert 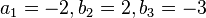 .
.
c) 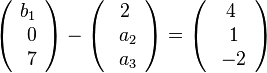 liefert
liefert 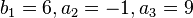
d) 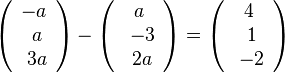 liefert
liefert
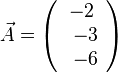 und
und 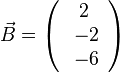
Buch S. 93 / 3b
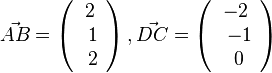
Buch S. 93 / 4
a) Die Punkte werden im Gegenuhrzeigersinn bezeichnet. Die untere Grundfläche hat die Punkte H, A, M, I, die obere Grundfläche die Punkte L, T, O, N. Also liegt H und L, A unter T, M unter O und I unter N.
T,O,N werden durch L(4;-4;0) zu einem Quadrat ergänzt.
O(0,0,0) und M(0,0,-4) bedeuten, dass die untere Fläche 4 unterhalb der oberen Fläche liegt.
Damit: T(4;0;0) liefert A(4;0;-4), N(0;-4;0) liefert I(0;-4;-4)
Nun ergeben sich noch H(4;-4;-4), A(4;0;-4), M(0,0,-4).
Also insgesamt: H(4;-4;4), A(4;0;-4), M(0;0;-4), I(0;-4;-4) und L((4;-4;0), T(4;0;0), O(0;0;0), N(0;-4;0)
Da O der Ursprung ist, ist ein Vektor 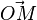 mit Startpunkt O der Ortsvektor
mit Startpunkt O der Ortsvektor 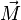 .
Fehler beim Parsen(Syntaxfehler): \vec {OM}= \vec M = \left ( \begin{array}{c} 0 \\\ 0 \\\ -4 \end{array}\right), \vec {OL} = \vec L = \left ( \begin{array}{c} 4 \\\ -4 \\\ 0 \end{array}\right), \vec {MH}=\vec H - \vec M = \left ( \begin{array}{c} 4 \\\ -4 \\\ 0 \end{array}\right), \vec {IA}=}vec A - \vec I = \left ( \begin{array}{c} 4 \\\ -4 \\\ 0 \end{array}\right)
.
Fehler beim Parsen(Syntaxfehler): \vec {OM}= \vec M = \left ( \begin{array}{c} 0 \\\ 0 \\\ -4 \end{array}\right), \vec {OL} = \vec L = \left ( \begin{array}{c} 4 \\\ -4 \\\ 0 \end{array}\right), \vec {MH}=\vec H - \vec M = \left ( \begin{array}{c} 4 \\\ -4 \\\ 0 \end{array}\right), \vec {IA}=}vec A - \vec I = \left ( \begin{array}{c} 4 \\\ -4 \\\ 0 \end{array}\right)
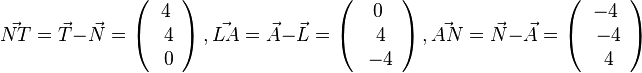
b) Die Pyramide hat ein Quadrat mit Seitenlänge a = 4 als Grundfläche und die Pyramidenhöhe 2, also ist