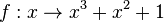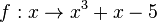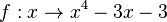M11 Das Newtonsche Iterationsverfahren: Unterschied zwischen den Versionen

Aus RSG-Wiki
Wechseln zu: Navigation, Suche
Zeile 9: Zeile 9:
 
In diesem [https://www.geogebra.org/m/sKQqtWq3 Applet] wird das Verfahren schrittweise dargestellt. }}
 
In diesem [https://www.geogebra.org/m/sKQqtWq3 Applet] wird das Verfahren schrittweise dargestellt. }}
  
−
{{Aufgaben-blau|2|2=Mache jeweils den ersten Schritt des Newton-Verfahrens für die Funktionen<br>
+
{{Aufgaben-blau|2|2=Machen Sie jeweils den ersten Schritt des Newton-Verfahrens für die Funktionen<br>
 +
Verwenden Sie jeweils als Startwert x<sub>0</sub> = 5.
 
a) <math>f:x \rightarrow x^3+x^2+1</math><br>
 
a) <math>f:x \rightarrow x^3+x^2+1</math><br>
 
b) <math>f:x \rightarrow x^3+x-5</math><br>
 
b) <math>f:x \rightarrow x^3+x-5</math><br>
 
c) <math>f:x \rightarrow x^4-3x-3</math><br>}}
 
c) <math>f:x \rightarrow x^4-3x-3</math><br>}}
  
−
{{Lösung versteckt|1=a) x1 = 0,4<br>
+
{{Lösung versteckt|1=a) x1 = 3,2235<br>
−
b) x1 = 1,75<br>
+
b) x1 = 3,3552<br>
−
c) x1 = 6 }}
+
c) x1 = 3,77876 }}
  
 
{{Aufgaben-blau|3|2=Ermitteln Sie jeweils alle Nullstellen der Funktion f nach dem Newton-Verfahren auf zwei Nachkommastellen genau.<br>
 
{{Aufgaben-blau|3|2=Ermitteln Sie jeweils alle Nullstellen der Funktion f nach dem Newton-Verfahren auf zwei Nachkommastellen genau.<br>
 +
Hierzu eignet sich eine Tabellenkalkulation!<br>
 
a) <math>f:x \rightarrow x^3+x^2+1</math><br>
 
a) <math>f:x \rightarrow x^3+x^2+1</math><br>
 
b) <math>f:x \rightarrow x^3+x-5</math><br>
 
b) <math>f:x \rightarrow x^3+x-5</math><br>
 
c) <math>f:x \rightarrow x^4-3x-3</math><br>}}
 
c) <math>f:x \rightarrow x^4-3x-3</math><br>}}
  
−
{{Lösung versteckt|1=a) x = - 1,466<br>
+
{{Lösung versteckt|1=a) x = - 1,46557<br>
−
b) x = 1,516<br>
+
b) x26 = 1,51598<br>
−
c) x = 1,685 }}
+
c) x7 = 1,6846 }}

Version vom 10. Dezember 2020, 15:24 Uhr

Für lineare und quadratische Funktionen hat man zur Bestimmung der Nullstellen Gleichungen zu lösen. Bei quadratischen Funktionen gibt es hierzu die Lösungsformel. Für Polynome höheren Grades kann man meist nur Nullstellen erraten und dann per Polynomdivision versuchen auf ein Polynom 2. Grades zu kommen.
Bei vielen Funktionen hat man Probleme die Nullstellen zu bestimmen. Oftmals reicht es aus, wenn man einen Näherungswert hat. Ein Verfahren um einen Näherungswert für die Nullstelle einer Funktion zu finden ist das Newtonsche Iterationsverfahren.


Bleistift 35fach.jpg   Aufgabe 1

Lesen Sie im Buch auf S.73 den gelb unterlegten Text durch. Schauen Sie sich danach die zwei Beispiele Auf S.73-74 an.

In diesem Video wird das Newton-Verfahren erkärt.

In diesem Applet wird das Verfahren schrittweise dargestellt.


Bleistift 35fach.jpg   Aufgabe 2

Machen Sie jeweils den ersten Schritt des Newton-Verfahrens für die Funktionen
Verwenden Sie jeweils als Startwert x0 = 5. a) f:x \rightarrow x^3+x^2+1
b) f:x \rightarrow x^3+x-5
c) f:x \rightarrow x^4-3x-3

a) x1 = 3,2235
b) x1 = 3,3552

c) x1 = 3,77876


Bleistift 35fach.jpg   Aufgabe 3

Ermitteln Sie jeweils alle Nullstellen der Funktion f nach dem Newton-Verfahren auf zwei Nachkommastellen genau.
Hierzu eignet sich eine Tabellenkalkulation!
a) f:x \rightarrow x^3+x^2+1
b) f:x \rightarrow x^3+x-5
c) f:x \rightarrow x^4-3x-3

a) x = - 1,46557
b) x26 = 1,51598

c) x7 = 1,6846
Von „http://rsg.zum.de/index.php?title=M11_Das_Newtonsche_Iterationsverfahren&oldid=10639“