M9 Zusammenfassung zum Lösen quadratischer Gleichungen: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „==Zusammenfassung wie man quadratische Gleichungen löst== {{Merksatz|MERK=Wie löst man eine quadratische Gleichung <math>ax^2+bx+c=0</math>? 1. Man kann e…“) |
(→Zusammenfassung wie man quadratische Gleichungen löst) |
||
| Zeile 11: | Zeile 11: | ||
i) Dazu bringt man zuerst die quadratische Gleichung, die sich bei der Lösung eines Problems ergibt auf die Form | i) Dazu bringt man zuerst die quadratische Gleichung, die sich bei der Lösung eines Problems ergibt auf die Form | ||
<center><math>ax^2+bx+c=0</math>,</center> | <center><math>ax^2+bx+c=0</math>,</center> | ||
| − | also man bringt alles auf die linke Seite. Auf der rechten Seite steht 0. Die linke Seite sortiert man nach x | + | also man bringt alles auf die linke Seite. Auf der rechten Seite steht 0. Die linke Seite sortiert man nach x<sup>2</sup>, x und der Zahl. |
ii) Wenn man ganz sicher gehen will notiert man sich a =, b=, c= und achtet dabei, dass man die Rechenzeichen als Vorzeichen zu den Zahlen nimmt. | ii) Wenn man ganz sicher gehen will notiert man sich a =, b=, c= und achtet dabei, dass man die Rechenzeichen als Vorzeichen zu den Zahlen nimmt. | ||
Version vom 10. Februar 2021, 12:36 Uhr
Zusammenfassung wie man quadratische Gleichungen löst
|
Merke:
Wie löst man eine quadratische Gleichung 1. Man kann es mit der Zerlegung in Linearfaktoren oder mit dem Satz von Vieta probieren. Dazu muss 2. Man findet immer die oder keine Lösung(en), wenn man die Lösungsformel anwendet. 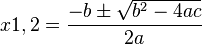 i) Dazu bringt man zuerst die quadratische Gleichung, die sich bei der Lösung eines Problems ergibt auf die Form 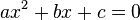 , ,also man bringt alles auf die linke Seite. Auf der rechten Seite steht 0. Die linke Seite sortiert man nach x2, x und der Zahl. ii) Wenn man ganz sicher gehen will notiert man sich a =, b=, c= und achtet dabei, dass man die Rechenzeichen als Vorzeichen zu den Zahlen nimmt. iii) Nun setzt man die Zahlen in die Lösungsformel ein. |

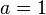 sein. Dann funktioniert es meistens sehr gut. Dann schaut man sich b und c an und findet durch einfaches Ausprobieren die Lösungen.
sein. Dann funktioniert es meistens sehr gut. Dann schaut man sich b und c an und findet durch einfaches Ausprobieren die Lösungen.
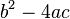 unter der Wurzel negativ ist, ist man fertig. Dann gibt es keine Lösung.
unter der Wurzel negativ ist, ist man fertig. Dann gibt es keine Lösung.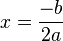 berechnet.
Wenn der Wert des Terms
berechnet.
Wenn der Wert des Terms 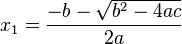 und
und 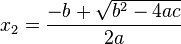 .
.

