10-Zusammenfassung Parameter bei den trigonometrischen Funktionen - Lösung
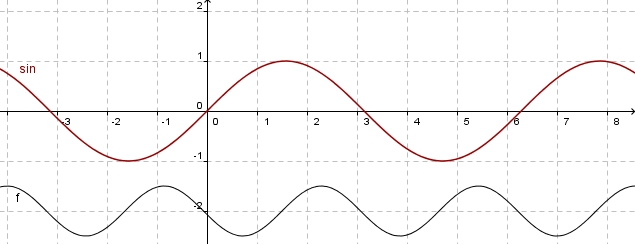
Ausgangspunkt ist dieses Bild:
Man sieht, dass der Graph um -2 (um 2 nach unten) entlang der y-Achse verschoben ist. Also ist d = -2. Also ist f(x) = a sin( bx + c )- 2.
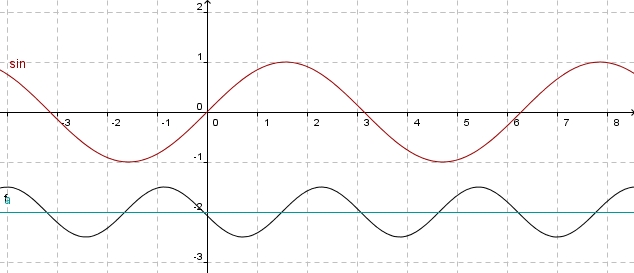
Die Sinuskurve verläuft um die Gerade y = -2, welche blau eingezeichnet ist.
Der Kurve ist außerdem in y-Richtung gestaucht. Man kann aus dem Koordinatensystem ablesen, dass a = 0,5 ist.
Also ist f(x) = 0,5 sin( bx + c ) - 2
Schwieriger wird es bei der Verschiebung entlang der x-Achse und der Stauchung in x-Richtung.
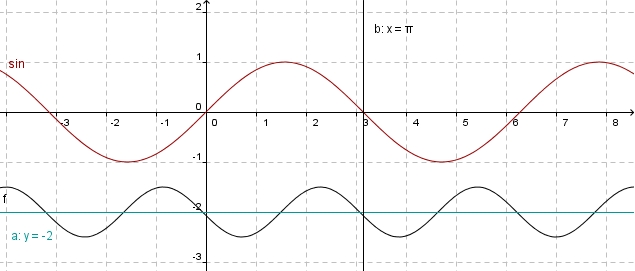
Zeichnet man die senkrechte Gerade x = PI ein, so erkennt man:
Wieso diese Gerade?
Bei x = PI hat die Sinusfuntion eine Nullstelle und die halbe Periodenlänge ist vorbei.
Die Sinuskurve ist um den Fakor 1/2 gestaucht. Also ist b = 2 und f(x) = 0,5 sin( 2x + c ) - 2
Was passiert mit der ersten Nullstelle (0;0) der Sinuskurve?
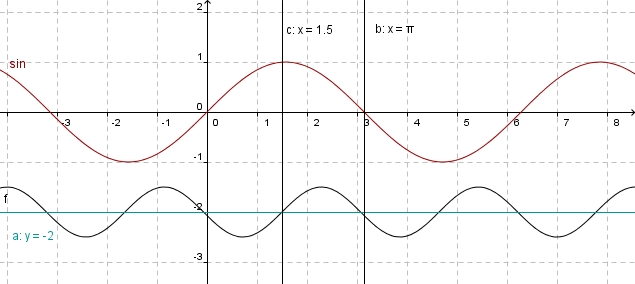
Zeichnet man die senkrechte Gerade x = 1,5 ein, so sieht man
dass diese Gerade die waagrechte Gerade y = -2 im Schnittpunkt mit dem Graphen von f schneidet. Also ist 0,5sin( 2(x-1,5)) - 2 = -2,
da sin( 2(x-1,5))= 0 ist.
Multipliziert man 2(x-1,5) aus, so erhält man 2x - 3.
Damit ist die Funktionsgleichung f(x) = 0,5 sin( 2x - 3 ) - 2.