Abstands- und Winkelbestimmungen
Dieses Thema ist im Buch auf S. 151 ausführlich beschrieben. Lesen Sie bitte diese Seite aufmerksam.
Die Hessesche Normalenform (HNF)
Aufgaben
S. 153/1
[Lösung anzeigen][Lösung ausblenden]
a) Die Ebene E hat als HNF 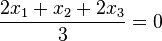 .
.
Der Ursprung O hat den Abstand von der Ebene E 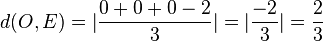 .
.
Man kann die Rechnung auch ohne Betragstriche machen. Ergibt sich ein negatives Ergebnis wie hiernimmt man hiervon den Betrag.
Der Abstand des Punktes P(6;-1;9) von der Ebene E ist 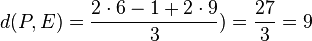
b) Die Ebene E hat als HNF 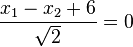 .
.
Der Ursprung O hat den Abstand von der Ebene E 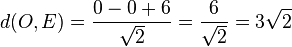 .
.
Der Punkt P(7;7;2) hat von E den Abstand 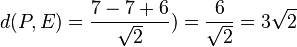 .
.
c) Die Ebene E hat als HNF 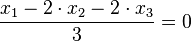 .
.
Der Ursprung O hat den Abstand von der Ebene E 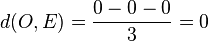 . Der Ursprung liegt in der Ebene E.
. Der Ursprung liegt in der Ebene E.
Der Punkt P(-1;1;3) hat von E den Abstand 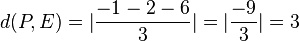 .
.
d) Die Ebene E hat als HNF 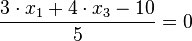 .
.
Der Ursprung O hat den Abstand von der Ebene E 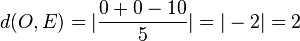 .
.
Der Punkt P(4;-1;2) hat von E den Abstand 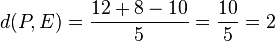 .
.
O und P liegen jeweils im Abstand 2 in verschiedenen Halbräumen zur Ebene E.
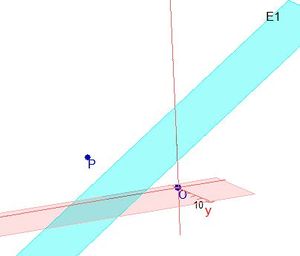
S. 153/2
[Lösung anzeigen][Lösung ausblenden]
(1) Wegen 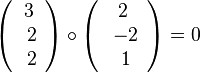 steht der Richtungsvektor
steht der Richtungsvektor  der Geraden g senkrecht zum Normalenvektor
der Geraden g senkrecht zum Normalenvektor  der Ebene E.
der Ebene E. 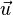 ist also komplanar zu den Richtungsvektoren der Ebene E.
ist also komplanar zu den Richtungsvektoren der Ebene E.
Die Ebene E hat als HNF 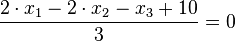 .
Für den Stützpunkt A(7;-13;-4) der Gerade g berechnet man
.
Für den Stützpunkt A(7;-13;-4) der Gerade g berechnet man 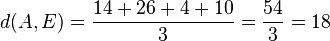 , also liegt A nicht in E und g ist echt parallel zu E. Das g echt parallel zu E ist, hat g auch den Abstand 18 zur Ebene E.
, also liegt A nicht in E und g ist echt parallel zu E. Das g echt parallel zu E ist, hat g auch den Abstand 18 zur Ebene E.
Wird g senkrecht auf E projeziert, dann wird in Richtung des Normalenvektors projeziert. Fällt man von A das Lot 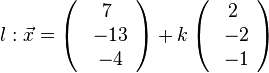 auf E, dann erhält man den Lotfusspunkt L durch 2(7+2k)-2(-13-2k)-(-4-k)+10=0 und k = -6 und L(-5;-1;2). Damit hat man für g* den Stützpunkt. Ihr Richtungsvektor ist derselbe wie bei g, da er "in E liegt" (ist komplanar zu den Richtungsvektoren von E). Die senkrechte Projektion von g in die Ebene E ist dann
auf E, dann erhält man den Lotfusspunkt L durch 2(7+2k)-2(-13-2k)-(-4-k)+10=0 und k = -6 und L(-5;-1;2). Damit hat man für g* den Stützpunkt. Ihr Richtungsvektor ist derselbe wie bei g, da er "in E liegt" (ist komplanar zu den Richtungsvektoren von E). Die senkrechte Projektion von g in die Ebene E ist dann 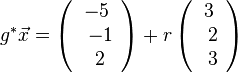 .
.
(2) Analog geht man hier vor.
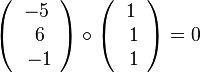 .
.
HNF von E: 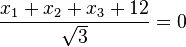 .
.
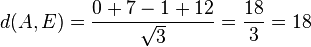
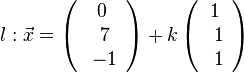
k + (7+k) + (-1+k) + 12 = 0 --> k = -6 und L(-6;1;-7)
S. 154/4
[Lösung anzeigen][Lösung ausblenden]
Die Ebene E hat HNF 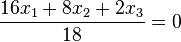 .
Für diese Gleichung hat man also einen Normaleneinheitsvektor
.
Für diese Gleichung hat man also einen Normaleneinheitsvektor 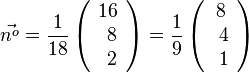 .
.
Zu einer zu E parallelen Ebene im Abstand 9 kommt man, wenn man neun mal diesen Normaleneinheitsvektor 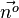 oder
oder 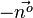 aneinandersetzt.
aneinandersetzt.
Deren HNF sind dann 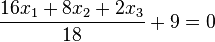 oder
oder 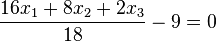 . (Berechnet man den Abstand des Ursprungs O (liegt in E) von diesen Ebenen kommt jeweils 9 heraus!)
. (Berechnet man den Abstand des Ursprungs O (liegt in E) von diesen Ebenen kommt jeweils 9 heraus!)
Schreibt man die Ebenengleichungen nur als Normalenform analog der Ebenengleichung für E, dann lauten sie 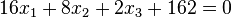 und
und 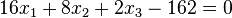 .
.
|
Bei gleichen Objekten (Gerade - Gerade) bzw. (Ebene - Ebene) wird cos zur Winkelberechnung verwendet. Bei ungleichen Objekten (Gerade - Ebene) wird sin zur Winkelberechnung verwendet. |
S. 154/6
[Lösung anzeigen][Lösung ausblenden]
a) Gleichsetzen der zwei Geradengleichungen liefert den Schnittpunkt (S(1;-1;0).
Für den Schnittwinkel interessieren nur die Richtungsvektoren der Geraden. Man erhält ihn aus 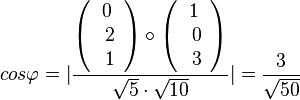 . Es ist
. Es ist 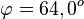 .
.
Ich lasse die Betragsstriche meist weg. Ist das Ergebnis für cos oder sin negativ, dann nimmt man einfach hier den Betrag
und erhält dann den spitzen Winkel.
b) S(0;2;-1) und 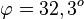
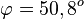
S. 154/7
[Lösung anzeigen][Lösung ausblenden]
a) Setzt man g in E ein, erhält man diese Gleichung 3(1+k) - (-2) - (-k) = 1 und k = -1. S(0;-2;1)
Für den Schnittwinkel interessieren der Richtungsvektor von g und der Normalenvektor der Ebene E. 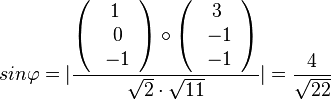 und
und 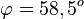
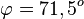
S. 154/8
[Lösung anzeigen][Lösung ausblenden]
a) Für den Schnittwinkel interessieren die zwei Normalenvektoren der Ebene. 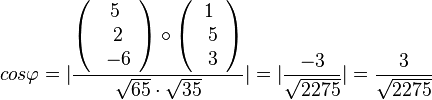 und
und 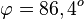
b) 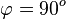
c) 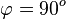
d) Hier ist es sinnvoll beide Ebenengleichungen in Normalenform zu schreiben;
E1: 5x1 - 6x2 - 2x3 + 3 = 0 und E2: 2x1 + x3 -3 = 0
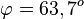
S. 154/9
[Lösung anzeigen][Lösung ausblenden]
a) Man hat die Gleichung 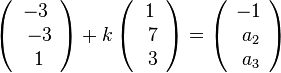
Aus der 1. Koordinatengleichung -3 + k = -1 folgt k = 2.
Für die 2. Koordinatengleichung ergibt sich -3 + 14 = a2, also a2=11.
Für die 3. Koordinatengleichung ergibt sich 1 + 6 = 3, also a3=7.
Also ist A(-1;11;7)
b) X ist ein Punkt auf g und hat dem Ortsvektor 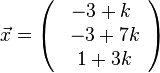 . Soll X Lotfusspunkt F des Lotes von P auf g sein, dann steht der Vektor
. Soll X Lotfusspunkt F des Lotes von P auf g sein, dann steht der Vektor 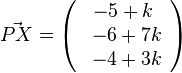 senkrecht auf dem Richtungsvektor
senkrecht auf dem Richtungsvektor  der Geraden. Also muss
der Geraden. Also muss 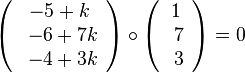 sein. Dies führt zur Gleichung
sein. Dies führt zur Gleichung
-5 + k + 7(-6 + 7k) + 3(-4+3k) = 0 und -59 + 59k = 0, also k = 1 und F(-2;4;4).
c) Den Spiegelpunkt A* von A bei Punktspiegelung am Zentrum Z = F(-2;4;4) erhält man durch 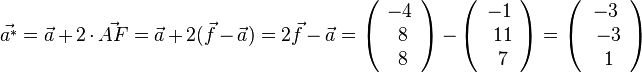 , also A*(-3;-3;1) .
, also A*(-3;-3;1) .
Analog erhält man P*(-6;5;3)
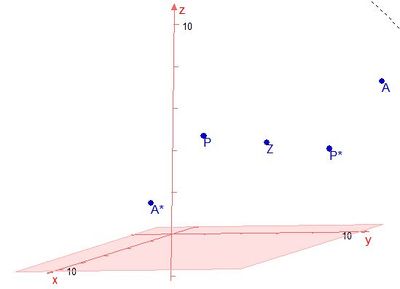
Den Flächeninhalt dieses Parallelogramms kann man nun berechnen.
elementar: Den Flächeninhalt eines Parallelogramms berechnet man mit der Formel A = g·h . Also muss man sich überlegen was ist g und was ist h. Die Punkte A, Z und A* liegen auf der Geraden g.
Man sieht, dass die beiden Dreiecke AA*P und AA*P* das Parallelogramm ergeben. Z = F ist der Lotfusspunkt des Lotes von P auf g, also ist die 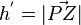 die Höhe des Dreiecks AA*P und
die Höhe des Dreiecks AA*P und 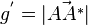 die Grundlinie des Dreiecks . Damit ergbit
die Grundlinie des Dreiecks . Damit ergbit 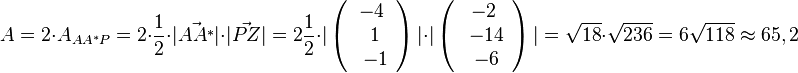
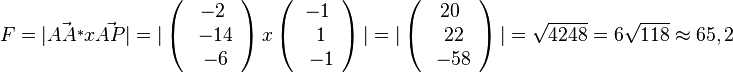
S. 155/10
[Lösung anzeigen][Lösung ausblenden]
a) Es ist 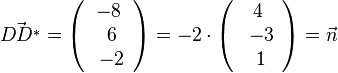 (
( ist der Normalenvektor der Ebene E), also steht der Vektor
ist der Normalenvektor der Ebene E), also steht der Vektor  senkrecht zur Ebene E.
senkrecht zur Ebene E.
Der Mittelpunkt M der Strecke [DD*] erhält man durch seinen Ortsvektor 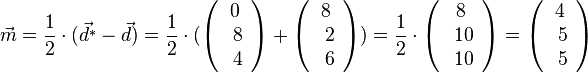 , also M(4;5;5) und M liegt wegen 4·4 - 3·4 + 5 -6 = 0 in der Ebene E, also sind die beiden Punkte D und D* symmetrisch zur Ebene E.
, also M(4;5;5) und M liegt wegen 4·4 - 3·4 + 5 -6 = 0 in der Ebene E, also sind die beiden Punkte D und D* symmetrisch zur Ebene E.
Man kann auch den Abstand der beiden Punkte von der Ebene E berechnen. Die HNF der Ebene E ist 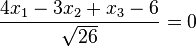
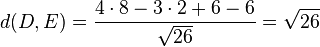 und
und 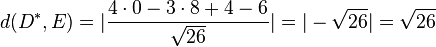 . Damit liegen D und D* auch symmetrisch zur Ebene E.
. Damit liegen D und D* auch symmetrisch zur Ebene E.
b) Das Vorgehen für die Spiegelung eines Punktes S an einer Ebene ist:
- Fälle von S das Lot auf die Ebene. Dabei ist das Lot l eine Gerade durch S in Richtung des Normalenvektors der Ebene E.
- Bestimme den Lotfußpunkt F als Schnittpunkt der Lotgeraden l mit der Ebene E.
- Den Spiegelpunkt erhält man, indem man den Verbindungsvektor der Punkte S und F über F hinaus nochmals anträgt.
c) Das Vorgehen ist in b) erklärt. Das Lot von P auf E schneidet die Ebene in F(3;1;2) und der Spiegelpunkt ist P*(-4;3;1).
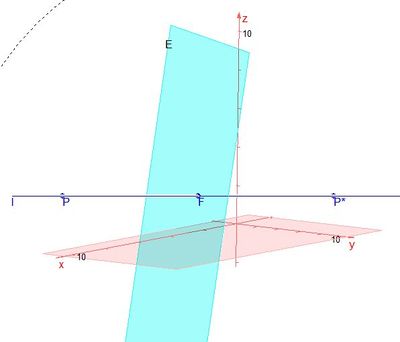
S. 155/12
[Lösung anzeigen][Lösung ausblenden]
S. 155/13
[Lösung anzeigen][Lösung ausblenden]
a) Der Mittelpunkt der Kugel ist der Ursprung M(0;0;0). Der Normalenvektor <marh>\vec{n}</math> der Ebene E ist 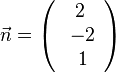 und hat den Betrag 3.
und hat den Betrag 3.
Mit der HNF der Ebene E kann man den Abstand von M zur Ebene E berechnen. Es ist 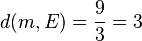 . Damit die Kugel die Ebene berührt muss ihr Radius 3 sein.
. Damit die Kugel die Ebene berührt muss ihr Radius 3 sein.
Den Berührpunkt erhält man, indem man von M aus ein Lot l auf E errichtet. Dieses Lot hat als Stützpunkt M und als Richtungsvektor den Normalenvektor der Ebene, also 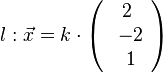 . Setzt man die Koordinaten von l in die Ebenengleichung, erhält man 2·2k - 2(-2k) + k - 9 = 0 und k = 1. Der Berührpunkt B hat die Koordinaten B(2;-2;1).
. Setzt man die Koordinaten von l in die Ebenengleichung, erhält man 2·2k - 2(-2k) + k - 9 = 0 und k = 1. Der Berührpunkt B hat die Koordinaten B(2;-2;1).
Analog geht man bei den Aufgaben b) und c) vor.
b) r = 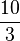 und
und 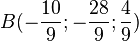 .
.
S. 155/15
[Lösung anzeigen][Lösung ausblenden]
a) Wie wir es schon öfter gemacht haben, macht man auch hier von Q ein Lot auf g. Der Lotfußpunkt F auf g hat einen Ortsvektor 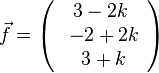 und der Vektor
und der Vektor 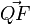 steht senkrecht auf dem Richtungsvektor
steht senkrecht auf dem Richtungsvektor 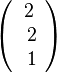 der Geraden g. Es ist also
der Geraden g. Es ist also 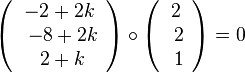 . Dies führt zur Gleichung 2(-2+2k) + 2(-8+2k) + 2+k =0 und k = 2 und F(7;2;5). Der Abstand der beiden Geraden ist dann
. Dies führt zur Gleichung 2(-2+2k) + 2(-8+2k) + 2+k =0 und k = 2 und F(7;2;5). Der Abstand der beiden Geraden ist dann 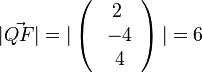 .
.
b) g und h spannen eine Ebene auf. g kann man gleich nehmen und man braucht noch einen zweiten Richtungsvektor, dafür eignet sich der Verbindungsvektor 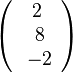 der beiden Stützpunkte, so dass sich diese Parameterdarstellung
der beiden Stützpunkte, so dass sich diese Parameterdarstellung 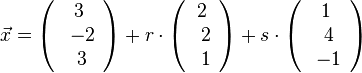 der Ebene E ergibt. Für die Normalenform der Ebenengleichung rechnet man zuerst
der Ebene E ergibt. Für die Normalenform der Ebenengleichung rechnet man zuerst 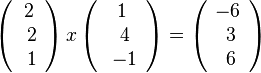 . Also ist
. Also ist 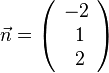 ein Normalenvektor und -2x1 + x2 + 2x3 + 2 = 0 .
ein Normalenvektor und -2x1 + x2 + 2x3 + 2 = 0 .
Den Schnittwinkel der Geraden k mit der Ebene E erhält man 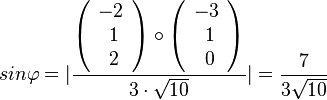 und
und 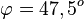 .
.
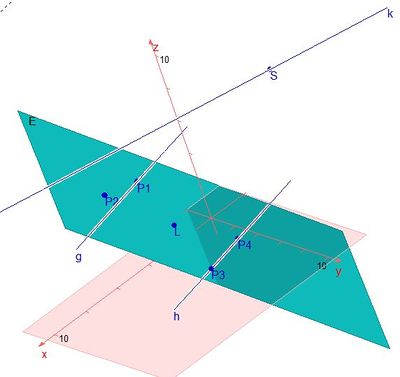
c) Gegeben ist eine gerade Pyramide. Dies bedeutet, dass die Spitze genau über dem Mittelpunkt des Grundquadrats ist.
Das Lot von S auf die Ebene E muss dann die Ebene auf der Mittelparallele m zu g und h schneiden. Der Mittelpunkt der Strecke [PQ] liegt auf dieser Mittelparallele. Es ist M(4;2;2) und 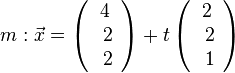 .
.
Macht man von einem passenden Punkt X auf m ein Lot zur Ebene, dann muss dieses Lot die Gerade k in S schneiden. Das Lot hat die Gleichung 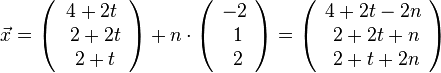 .
.
Setzt man das Lot gleich k, dann hat man ein Gleichungssystem von drei Gleichungen mit 3 Unbekannten.
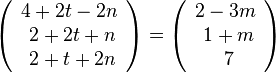
Wenn man dies löst, erhält man Lösungen m = 2, n = 3, t = -1.
m = 2 liefert S(-4;3;7), n = 3 würde die Höhe der Pyramide liefern (interessiert hier aber nicht!), t = -1 liefert den Lotfußpunkt L(2;0;1). (Die Gerade SL steht senkrecht zur Ebene E!)
L ist Mittelpunkt des Grundquadrats (es handelt sich um eine gerade Pyramide.). Nun macht man ein Lot auf g und h. In a) hat man sich schon überlegt, dass der Vektor 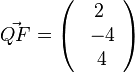 ist. Also muss man von L den halben Vektor jeweils zur einen und zur anderen Seite gehen um auf g und h zu kommen.
ist. Also muss man von L den halben Vektor jeweils zur einen und zur anderen Seite gehen um auf g und h zu kommen.
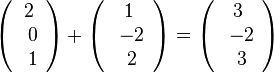 F1(3;-2;3) auf g und
F1(3;-2;3) auf g und 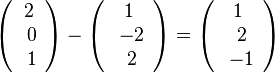 F2(1;2;-1) auf h.
F2(1;2;-1) auf h.
Da die Geraden g und h den Abstand 6 haben, muss man nun von den Punkten F1 und F2 noch 3 Einheiten auf g und h jeweils in verschiedene Richtungen der Geraden gehen und man hat die Eckpunkte der Pyramide. Da der Richtungsvektor von g und h Betrag 3 hat, nimmt man hier statt einem Einheitsvektor gleich den Richtungsvektor.
Die Eckpunkte der Pyramide werden mit P1, P2, P3 und P4 bezeichnet. Es ist dann:
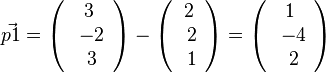 , also P1(1;-4;2)
, also P1(1;-4;2)
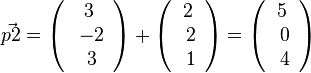 , also P2(5;0;5)
, also P2(5;0;5)
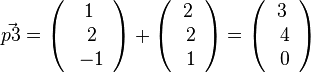 , also P3(3;4;0)
, also P3(3;4;0)
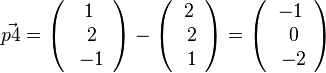 , also P4(-1;0;-2)
, also P4(-1;0;-2)
S. 156/16
[Lösung anzeigen][Lösung ausblenden]
Die Ebene E hat Normalenvektor 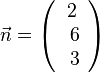 . Der Normaleneinheitsvektor ist
. Der Normaleneinheitsvektor ist 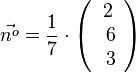 . Der Radius der Kugel ist 7. Geht man nun von S aus 7 mal in Richtung
. Der Radius der Kugel ist 7. Geht man nun von S aus 7 mal in Richtung 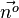 oder
oder 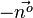 , dann erhält man die zwei Mittelpunkte M und M*.
, dann erhält man die zwei Mittelpunkte M und M*.
Also 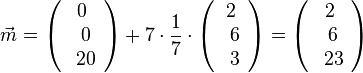 und M(2;6;23)
und M(2;6;23)
Also 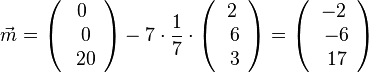 und M(-2;-6;17).
und M(-2;-6;17).
b) Die Gerade m hat als Stützpunkt M und ihr Richtungsvektor ist der Vektor 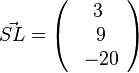 . Damit ist
. Damit ist 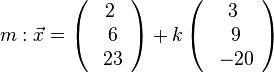 .
.
c) Die Ebene E* ist parallel zur x1x2-Ebene im Abstand 7 (Radius der Kugel), also x3 - 7 = 0 .
Setzt man die x3-Koordinate von m in die Ebenengleichung ein erhält man 23 - 20k - 7 = 0 und 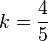 . Die Koordinaten von T erhält man, wenn man diesen Wert von k in die Geradengleichung von m einsetzt, also T(4,4;13,2;7) .
. Die Koordinaten von T erhält man, wenn man diesen Wert von k in die Geradengleichung von m einsetzt, also T(4,4;13,2;7) .
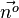 zu M gegangen. Nun erhält man den Berührpunkt, wenn man von T aus 7 mal in Richtung
zu M gegangen. Nun erhält man den Berührpunkt, wenn man von T aus 7 mal in Richtung 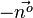 geht. Dann ist
geht. Dann ist 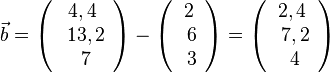 und B(2,4;7,2;4).
und B(2,4;7,2;4).
