M10 Die Exponentialfunktion
Bei den Beispielen zum exponentiellen Wachstum war der Term immer von der Form 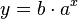 . Dabei war b der Anfangsbestand und a der Wachstumsfaktor. Diese Gleichung beschreibt einen neuen Funktionstyp. Bei diesen Funktionen steht die Variable x im Exponenten, daher heißen diese Funktionen Exponentialfunktionen.
. Dabei war b der Anfangsbestand und a der Wachstumsfaktor. Diese Gleichung beschreibt einen neuen Funktionstyp. Bei diesen Funktionen steht die Variable x im Exponenten, daher heißen diese Funktionen Exponentialfunktionen.
|
Merke:
Die Funktion 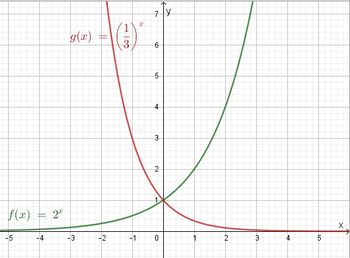 Der Graph ist eine Exponentialkurve. |
Aus den Beispielen kennst du, dass x irgendeine reelle Zahl, also eine negative oder positive Zahl oder 0 sein kann.
Wenn a=0 wäre, was ist dann 0^0 oder 0-1?
00 ist nicht definiert, ebenso wäre 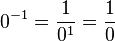 ein nicht definierter Term.
ein nicht definierter Term.
Wenn a eine negative Zahl wäre, z.B. a = -2, was ist dann 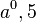 ?
?
Für a = -2 hätte man den Term 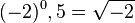 , was in den reellen Zahlen nicht möglich ist, dies ist nicht definiert.
, was in den reellen Zahlen nicht möglich ist, dies ist nicht definiert.
2. Wenn a > 1 ist, dann hat man eine monoton steigenden Graphen, wenn a < 1 ist, dann ist der Graph monoton fallend.
3. Alle Graphen haben den Punkt (0;1) gemeinsam.
4. Es ist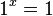 , daher ist diese Funktion die konstante 1, also die Funktion, die jedem x fir Zahl 1 zuordnet.
, daher ist diese Funktion die konstante 1, also die Funktion, die jedem x fir Zahl 1 zuordnet.30px Merke
Bei einem Funktionsgraphen geht man bei der Betrachtung immer in x-Richtung von links nach rechts, d.h. die x-Werte nehmen zu, sie werden größer. 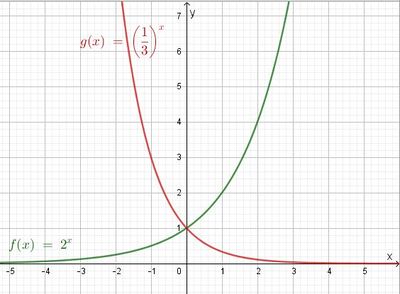 Beim grünen Graphen werden die y-Werte immer größer, wenn die x-Werte auch größer werden, der grüne Graph ist streng monoton steigend, |
a) 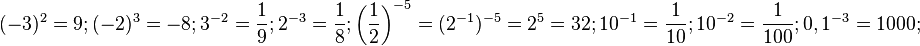
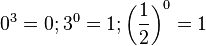
b) ![25^{\frac{1}{2}}=\sqrt 25 = 5; 25^{-\frac{1}{2}}=\frac{1}{5}=0,2; 9^{\frac{3}{2}}=27; 0,125^{\frac{1}{3}}=0,5; 0,125^{-\frac{2}{3}}=4; 4^{0,5}=\sqrt 4 = 2; 32^{0,2}=32^{\frac{1}{5}}=\sqrt [5] {32}=2;](/images/math/f/9/6/f9636ee63fe20e270dc910e8abd0d2f4.png)
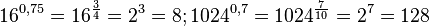
c) Ein Bruch als Exponent ist z.B.  . Dies bedeutet, dass man aus der Basis die Wurzel zieht. Unter der Wurzel darf aber keine negative Zahl stehen, also darf die Basis nicht negativ sein. Die Basis ist deshalb positiv oder 0.
. Dies bedeutet, dass man aus der Basis die Wurzel zieht. Unter der Wurzel darf aber keine negative Zahl stehen, also darf die Basis nicht negativ sein. Die Basis ist deshalb positiv oder 0.
d) ... = 4
e) 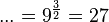
f) ... = 0,25-0,5 = 0,5-1 = 2
g) 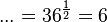
h) ... = 5-1 = 0,2
i) ... 32-0,4 = 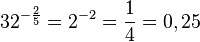
k) 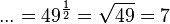
l) 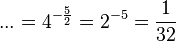
m) 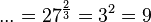
n) ... = (9 - 4)-2 = 5-2 = 0,04
o) 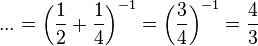
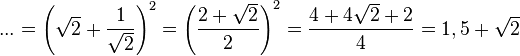
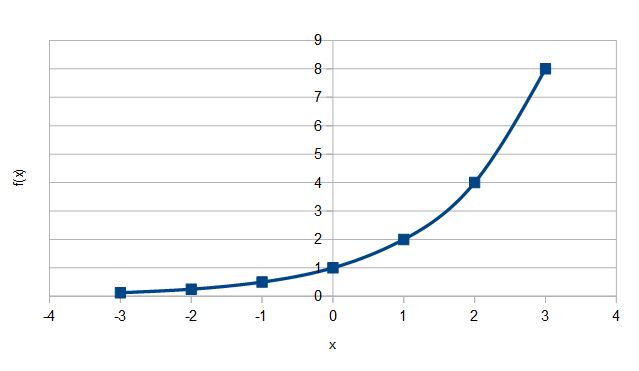
c) Die Funktionswerte f(x) werden, wenn man nach links geht immer kleiner und nähern sich 0 an. Wenn man nach rechts geht, werden die Funktionswerte f(x) immer größer.
Wenn man nach links geht, erhält man den nächsten Funktionswert f(x-1), indem man den Funktionswert f(x) durch 2 dividiert.
Wenn man nach rechts geht, erhält man den nächsten Funktionswert f(x+1), indem man den Funktionswert f(x) mit 2 multipliziert.
d) 
Es sind die gleichen Funktionswerte nur absteigend, also in umgekehrter Reihenfolge.
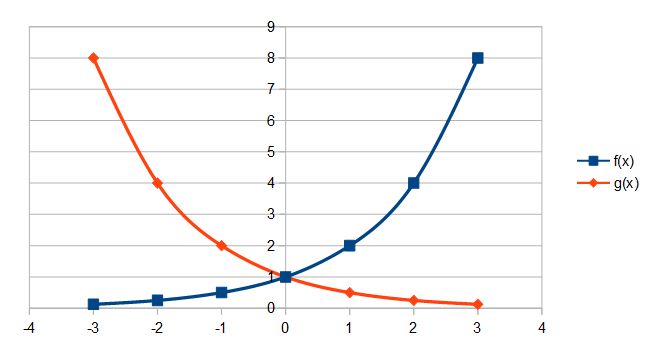
Die Graphen sind achsensymmetrisch zur y-Achse.

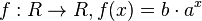 (b ∈ R+\{0}, a ∈ R+) heißt Exponentialfunktion zur Basis a.
(b ∈ R+\{0}, a ∈ R+) heißt Exponentialfunktion zur Basis a.
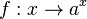 gemeinsam?
gemeinsam?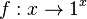 ?
?
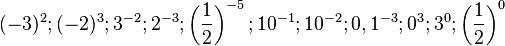
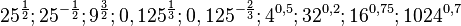
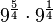
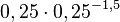
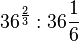
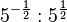
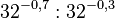
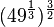
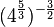
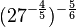
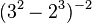
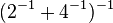
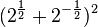
 mit
mit 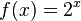 .
. 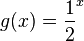 .
.