M10 Wahrscheinlichkeitsrechnung
Inhaltsverzeichnis |
Mehrstufige Zufallsexperimente
In der neunten Klasse habt ihr schon mehrstufige Zufallsexperimente behandelt.
|
Merke:
Es gelten bei mehrstufgen Zufallsexperimenten die drei Pfadregeln: 1. Der Summenwert der Wahrscheinlichkeiten auf den Teilpfaden, die von einem Verzweigungspunkt ausgehen, ist 1. 2. Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem produtk der Wahrscheinlichkeiten auf dem Pfad, der zu diesem Ergebnis führt. 3. Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten für die zugehörigen Ergebnisse. |
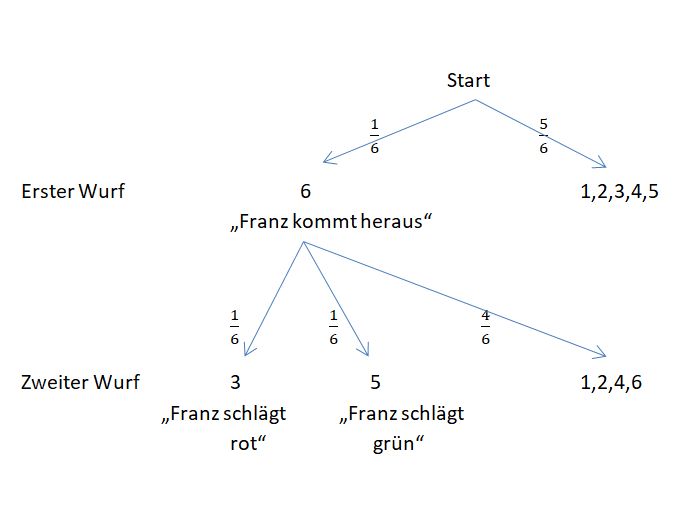
Beim Spiel "Mensch ärgere dich nicht" hat man für Franz folgende Situation, die im Baumdiagramm veranschaulicht ist:
Die erste Pfaderegel bedeutet hier, dass vom oberen Verzweigungspunkt ("Franz kommt heraus oder kommt nicht heraus.") die Summe 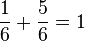 ist.
ist.
Für den Verzweigungspunkt "6" bedeutet dies 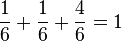
Die zweite Pfadregel bedeutet hier für das Ergebnis "Franz kommt heraus und schlägt rot.", dass die Wahrscheinlichkeit für dieses Ergebnis 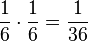 ist.
ist.
Für das Ergebnis "Franz kommt heraus und schlägt grün." ist die Wahrscheinlichkeit 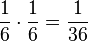 .
.
Mit der dritten Pfadregel erhält man für das Ereignis "Franz kommt heraus und schlägt die rote oder grüne Spielfigur" die Wahrscheinlichkeit 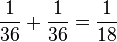 .
.
70/1a  = {RRR, RRW, RWR, RWW, WRR, WRW, WWR}
= {RRR, RRW, RWR, RWW, WRR, WRW, WWR}
b) 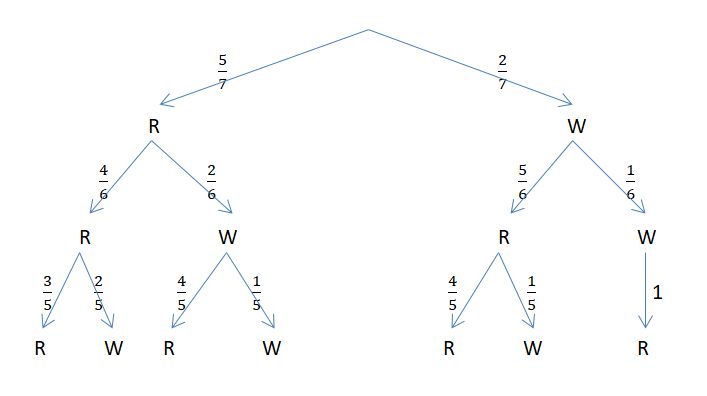
c) P({RRR}) = 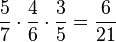
d) P("beide weiße Kugeln") = P({RWW, WRW, WWR})= 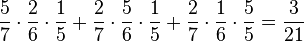
70/2a 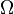 = {RRR, RRW, RWR, RWW, WRR, WRW, WW}
= {RRR, RRW, RWR, RWW, WRR, WRW, WW}
b) 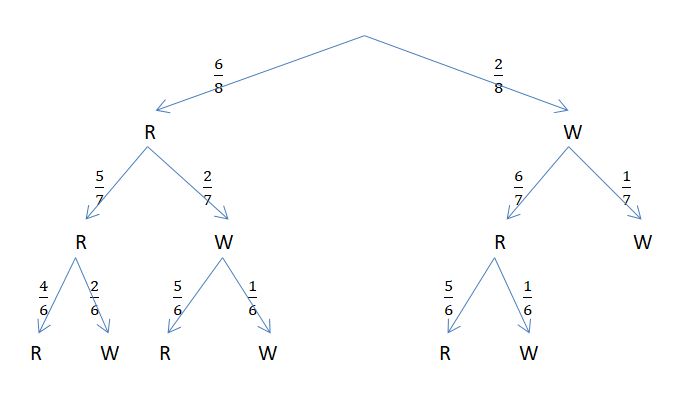
c) geschätzt: ?
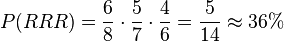 , also kleiner als 50%.
, also kleiner als 50%.
Man sieht an dem Eingangsbeispiel und den zwei Aufgaben, dass ein weitergehendes Experiment vom vorherigen Ausgang abhängen kann.
Bei "Mensch ärgere dich nicht" kann Franz nur weiterwürfeln, wenn er "6" gewürfelt hat.
Bei den Aufgaben sieht man, dass wenn zwei weiße Kugeln gezogen sind, nur noch rote Kugeln gezogen werden können.
Der weitere Versuchsverlauf hängt also von dem bisherigen Ergebnis/den bisherigen Ergebnissen ab.
Wir betrachten nun die Wahrscheinlichkeiten am Baumdiagramm an folgendem Beispiel:
Max und Moritz ziehen aus einer Lostrommel mit 5 Losen, wobei 2 Gewinnlose und 3 Nieten sind, jeweils ein Los. Max möchte anfangen. Die Trefferwahrscheinlichkeit, das ist die Wahrscheinlichkeit, dass Max ein Gewinnlos zieht, ist für Max dann 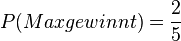 .
.
Moritz fühlt sich benachteiligt und sagt: "Wenn Max gezogen hat, sind nur noch 1 Gewinnlos, aber 3 Nieten in der Lostrommel und meine Trefferwahrscheinlichkeit ist 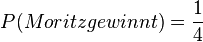 ." Fühlt sich Moritz zu Recht benachteiligt?
." Fühlt sich Moritz zu Recht benachteiligt?
Im Baumdiagramm schaut das so aus:
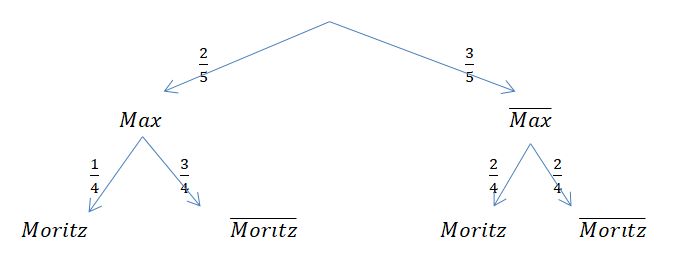
Im Baumdiagramm sieht man, dass sich die Wahrscheinlichkeit, dass Moritz ein Gewinnlos zeiht aus zwei Ergebnissen besteht, deren Einzelwahrscheinlichkeiten dann adiiert werden. Es ist 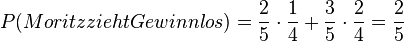 . Man spricht hier von der totalen Wahrscheinlichkeit P(Moritz zieht Gewinnlos).
. Man spricht hier von der totalen Wahrscheinlichkeit P(Moritz zieht Gewinnlos).
Die Wahrscheinlichkeit  , die Moritz in seiner Rechnung berechnet hat, beruht darauf, dass Max schon ein Gewinnlos gezogen hat, dass also schon eine Bedingung vorher eingetreten ist. Daher nennt man diese Wahrscheinlichkeit bedingte Wahrscheinlichkeit
, die Moritz in seiner Rechnung berechnet hat, beruht darauf, dass Max schon ein Gewinnlos gezogen hat, dass also schon eine Bedingung vorher eingetreten ist. Daher nennt man diese Wahrscheinlichkeit bedingte Wahrscheinlichkeit 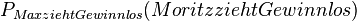 .
.
30px Merke
Ist Das Ereignis A eingetreten, dann wird die Wahrscheinlichkeit, dass danach das Ereignis B eintritt als bedingte Wahrscheinlichkeit bezeichnet und sie wird als
|
Moritz hat also eine bedingte Wahrscheinlichkeit berechnet. Für seine Chancen ein Gewinnlos zu ziehen ist aber die totale Wahrscheinlichkeit maßgeblich und die ist genauso groß als wie wenn Max anfängt. Also haben Max und Moritz beide die gleiche Wahrscheinlichkeit ein Gewinnlos zu ziehen.
71/3a) Es handelt sich nicht um ein Laplace-Experiment, da die beiden Ergebnisse R und W nicht gleichwahrscheinlich sind. Es ist 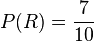 und
und 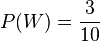 .
.
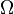 = {RR, RW, WR, WW}
= {RR, RW, WR, WW}
b) 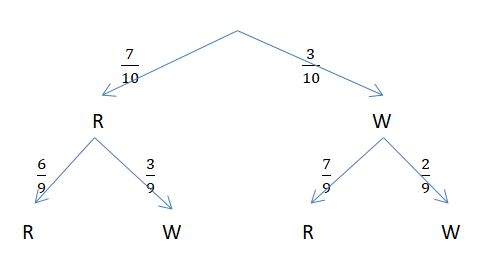
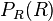 ist die Wahrscheinlichkeit, dass man beim zweiten Zug eine rote Kugel zieht, wenn man beim ersten Zug schon eine rote Kugel gezogen hatte. Eine rote Kugel ist beim ersten Zug weg. Also sind nur noch 9 Kugeln in der Urne. Dann ist
ist die Wahrscheinlichkeit, dass man beim zweiten Zug eine rote Kugel zieht, wenn man beim ersten Zug schon eine rote Kugel gezogen hatte. Eine rote Kugel ist beim ersten Zug weg. Also sind nur noch 9 Kugeln in der Urne. Dann ist 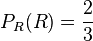 , da von den restlichen 9 Kugel 6 rot sind.
, da von den restlichen 9 Kugel 6 rot sind.
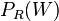 ist die Wahrscheinlichkeit, dass man beim zweiten Zug eine weiße Kugel zieht, wenn man beim ersten Zug schon eine rote Kugel gezogen hatte. Eine rote Kugel ist beim ersten Zug weg. Dann ist
ist die Wahrscheinlichkeit, dass man beim zweiten Zug eine weiße Kugel zieht, wenn man beim ersten Zug schon eine rote Kugel gezogen hatte. Eine rote Kugel ist beim ersten Zug weg. Dann ist 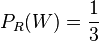 , da von den restlichen 9 Kugeln 3 weiß sind.
, da von den restlichen 9 Kugeln 3 weiß sind.
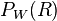 ist die Wahrscheinlichkeit, dass man beim zweiten Zug eine rote Kugel zieht, wenn man beim ersten Zug schon eine weiße Kugel gezogen hatte. Eine weiße Kugel ist beim ersten Zug weg. Dann ist
ist die Wahrscheinlichkeit, dass man beim zweiten Zug eine rote Kugel zieht, wenn man beim ersten Zug schon eine weiße Kugel gezogen hatte. Eine weiße Kugel ist beim ersten Zug weg. Dann ist 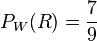 , da von den restlichen 9 Kugeln 7 rot sind.
, da von den restlichen 9 Kugeln 7 rot sind.
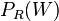 ist die Wahrscheinlichkeit, dass man beim zweiten Zug eine weiße Kugel zieht, wenn man beim ersten Zug schon eine weiße Kugel gezogen hatte. Eine weiße Kugel ist beim ersten Zug weg. Dann ist
ist die Wahrscheinlichkeit, dass man beim zweiten Zug eine weiße Kugel zieht, wenn man beim ersten Zug schon eine weiße Kugel gezogen hatte. Eine weiße Kugel ist beim ersten Zug weg. Dann ist 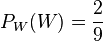 , da von den restlichen 9 Kugeln 2 weiß sind.
, da von den restlichen 9 Kugeln 2 weiß sind.
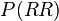 ist die Wahrscheinlichkeit für das Ereignis, dass beim ersten und zweiten Zug jeweils eine rote Kugel gezogen wurde. Nach der 2. Pfadregel ist
ist die Wahrscheinlichkeit für das Ereignis, dass beim ersten und zweiten Zug jeweils eine rote Kugel gezogen wurde. Nach der 2. Pfadregel ist 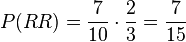
Für die Wahrscheinlichkeit 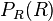 wurde beim ersten Zug bereits eine rote Kugel gezogen und sie gibt nun an, mit welcher Wahrscheinlichkeit nun beim zweiten Zug eine rote Kugel gezogen wird. Es ist
wurde beim ersten Zug bereits eine rote Kugel gezogen und sie gibt nun an, mit welcher Wahrscheinlichkeit nun beim zweiten Zug eine rote Kugel gezogen wird. Es ist 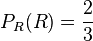 .
.
c) Dieses Ereignis besteht aus den zwei Ergebnissen RW und WR. Nach der 3. Pfadregel ist 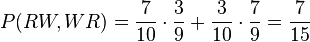
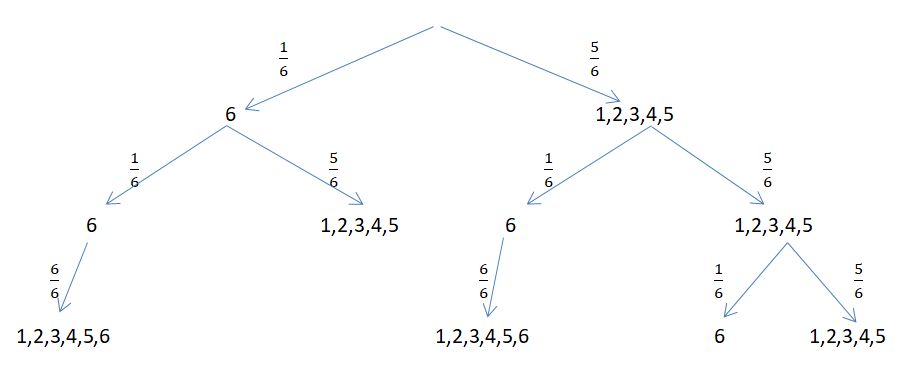
71/4a Würfelt der Spieler gleich beim ersten Mal eine 6, dann darf er raus und nochmals würfeln. Hat er erneut eine 6 würfelt er nochmal, ansonsten würfelt er nicht mehr. Hat er beim ersten Mal keine 6 gewürfelt, dann darf er trotzdem nochmals würfeln.
Würfelt er nun beim zweiten Mal eine 6, dann darf er raus und nochmals würfeln. Für den nächsten Wurf ist es egal was er hat.
Hat er auch beim zweiten Mal keine 6 gewürfelt, dann darf er nochmals würfeln. Würfelt er jetzt eine 6, dann darf er raus und nochmals würfeln. Wenn er auch beim dritten Mal keine 6 gewürfelt hat, gibt er den Würfel an den nächsten Spieler weiter.
b) Erfahrungsgemäß erwarte ich, dass die Wahrscheinlichkeit kleiner als 0,5 ist.
c) 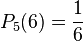
Das dreimalige Werfen eines Würfels entspricht dem dreimaligen Ziehen aus einer Urne mit Zurücklegen. Man hat also beim zweiten Versuch die gleichen Bedingungen wie beim ersten Versuch. Eine 6 zu werfen ist ein günstiger Fall von sechs möglichen Fällen.
d) Ein Baumdiagramm könnte so aussehen:
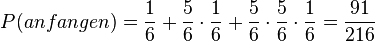
Beim Schafkopf-Spiel gibt es 32 Karten, dabei sind 4 Farben und jede Farbe hat 8 Karten.
a) 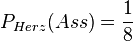 , da es nur 1 Ass unter den 8 Herz-Karten gibt.
, da es nur 1 Ass unter den 8 Herz-Karten gibt.
Die Bedingung ist, dass man nur Herz-Karten betrchtet und aus den Herz-Karten dann die Ass ziehen will.
b) 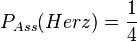 , da es es unter den 4 Assen nur 1 Herz-Ass gibt.
, da es es unter den 4 Assen nur 1 Herz-Ass gibt.
Hier ist die Bedingung, dass man die Asse hat und nun die Herz-Ass ziehen will.
c) 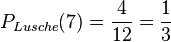 , da es es unter den 12 Luschen 4 7-Karten gibt.
, da es es unter den 12 Luschen 4 7-Karten gibt.
d) 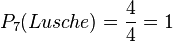 , da alle 4 7-Karten Luschen sind.
, da alle 4 7-Karten Luschen sind.
e)  , da es unter den 12 Luschen 4 7-Karten und 4 8-Karten gibt.
, da es unter den 12 Luschen 4 7-Karten und 4 8-Karten gibt.
f) 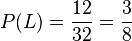 ist die Wahrscheinlichkeit eine Lusche zu ziehen.
ist die Wahrscheinlichkeit eine Lusche zu ziehen.
g) 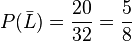 ist die Wahrscheinlichkeit keine Lusche zu ziehen.
ist die Wahrscheinlichkeit keine Lusche zu ziehen.
h) 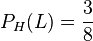 ist die Wahrscheinlichkeit aus den 8 Herzkarten eine der 3 Luschen zu ziehen.
ist die Wahrscheinlichkeit aus den 8 Herzkarten eine der 3 Luschen zu ziehen.
i) 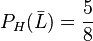 ist die Wahrscheinlichkeit aus den 8 Herzkarten keine Lusche zu ziehen.
ist die Wahrscheinlichkeit aus den 8 Herzkarten keine Lusche zu ziehen.
k) 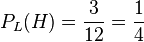 ist die Wahrscheinlichkeit aus den 12 Luschen eine der drei Herz-Luschen zu ziehen.
ist die Wahrscheinlichkeit aus den 12 Luschen eine der drei Herz-Luschen zu ziehen.
l) 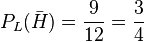 ist die Wahrscheinlichkeit aus den 12 Luschen keine Herz-Lusche zu ziehen. Von jeder Farbe gibt es 3 Luschen, also von den anderen drei Farben insgesamt 9 Luschen.
ist die Wahrscheinlichkeit aus den 12 Luschen keine Herz-Lusche zu ziehen. Von jeder Farbe gibt es 3 Luschen, also von den anderen drei Farben insgesamt 9 Luschen.
m) 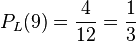 ist die Wahrscheinlichkeit eine der 4 9-Karten aus den 12 Luschen zu ziehen.
ist die Wahrscheinlichkeit eine der 4 9-Karten aus den 12 Luschen zu ziehen.
n) 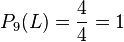 ist die Wahrscheinlichkeit aus den 4 9-Karten eine Lusche zu ziehen. (Alle 4 9-Karten sind Luschen!)
ist die Wahrscheinlichkeit aus den 4 9-Karten eine Lusche zu ziehen. (Alle 4 9-Karten sind Luschen!)
o) 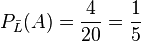 ist die Wahrscheinlichkeit aus den 20 Nicht-Luschen eine der 4 Assen zu ziehen.
ist die Wahrscheinlichkeit aus den 20 Nicht-Luschen eine der 4 Assen zu ziehen.
p) 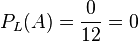 ist die Wahrscheinlicheit eine Ass aus den Luschen zu ziehen. Bei den Luschen kommt aber keine Ass vor!
ist die Wahrscheinlicheit eine Ass aus den Luschen zu ziehen. Bei den Luschen kommt aber keine Ass vor!
q) 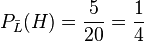 ist die Wahrscheinlichkeit aus den 20 Nicht-Luschen eine der 5 Herz-Karten zu ziehen.
ist die Wahrscheinlichkeit aus den 20 Nicht-Luschen eine der 5 Herz-Karten zu ziehen.
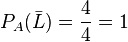 ist die Wahrscheinlichkeit eine Nicht-Lusche aus den 4 Assen zu ziehen. Alle 4 Asse sind Nicht-Luschen!
ist die Wahrscheinlichkeit eine Nicht-Lusche aus den 4 Assen zu ziehen. Alle 4 Asse sind Nicht-Luschen!
Mit der Vierfeldertafel kann man ähnliche Fragestellungen beantworten.
In der Klasse gibt es 12 Mädchen und 20 Jungs. von den 32 Schülerinnen und Schüler haben 8 eine Brille, 24 tragen keine Brille.
a) 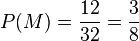
b) 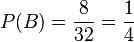
c) Das Mädchen trägt auch Brille. Davon gibt es 4 in der Klasse, also 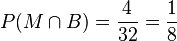 .
.
d) Aus den 12 Mädchen wird eine Brillenträgerin ausgewählt. 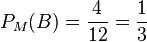
e) Aus den 20 Jungs wird ein Brillenträger ausgewählt. 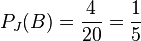
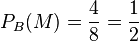
Bedingte Wahrscheinlichkeit
Im ersten Teil dieser Seite wurden bedingte Wahrscheinlichkeiten stets aus dem Baumdiagramm erkannt als Wahrscheinlichkeiten nach einem Verzweigungspunkt. Das war einfach.
Schaue das Video
In diesem Video ist es am Ende etwas konfus, aber es stellt sich nun die Frage:
Wie groß ist der Anteil der Jungs (Mädchen) unter denen die Mathe mögen?
Die Frage lässt sich nicht auf den ersten Blick aus dem Baumdiagramm im Video lösen.
Das Baumdiagram zum Beispiel im Video ist
M bezeichnet "Mathe mögen", 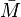 bezeichnet "Mathe nicht mögen"
bezeichnet "Mathe nicht mögen"
J bezeichnet "Jungs", 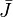 bezeichent "Mädchen".
bezeichent "Mädchen".
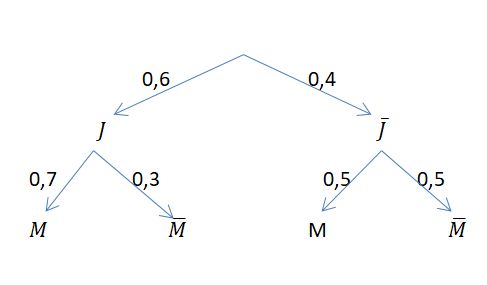
Hier ist klar, dass von den Jungs 70% Mathe mögen, bei den Mädchen sind es 50%. Das sind die bedingten Wahrscheinlichkeiten 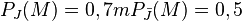
Doch was ist mit der umgekehrten Fragestellung? Wie groß ist der Anteil der Jungs bzw. Mädchen, die Mathe mögen?
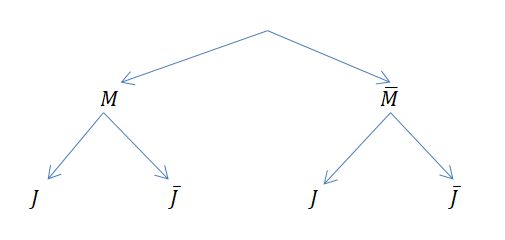
Welche Wahrscheinlichkeiten trägt man in dieses Baumdiagramm ein?
Aus dem Video erhält man, dass 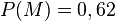 und
und 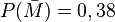 ist. Doch welche Wahrscheinlichkeiten werden nach den Verzweigungspunkten
ist. Doch welche Wahrscheinlichkeiten werden nach den Verzweigungspunkten 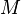 und
und 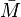 eingetragen?
eingetragen?
Um hierzu eine Lösung zu finden schauen wir uns nochmals das Baumdiagramm aus dem Film an:

Die Wahrscheinlichkeit dass ein Junge Mathe mag ist nach der 2. Pfadregel 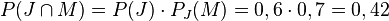
Überträgt man diese Überlegung auf das neue Baumdiagramm

dann ist 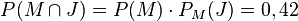 und nach
und nach 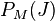 aufgelöst
aufgelöst 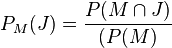 .
.
Im Video erhielt man für 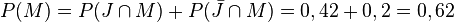 , also ist
, also ist 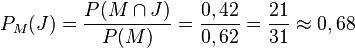 .
.
Also sind unter den Schülern, die "Mathe mögen" 68% Jungs und 32% Mädchen.
|
Merke:
Die bedingte Wahrscheinlichkeit 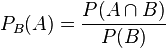 |
In diesem Video wird bedingte Wahrscheinlichkeit in Zusammenhang mit Baumdiagramm und Vierfeldertafel nochmals erklärt.
a) 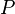 "Person ist infiziert",
"Person ist infiziert", 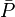 "Person ist nicht infiziert.
"Person ist nicht infiziert.
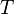 "Test ist positiv",
"Test ist positiv", 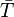 "Test ist negativ"
"Test ist negativ"
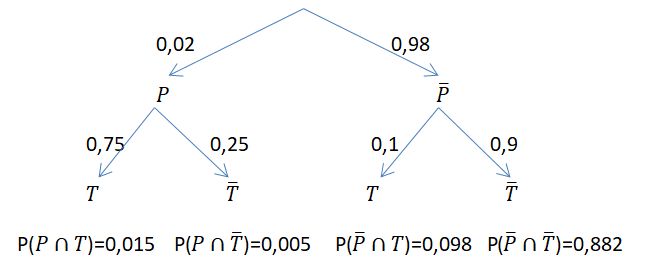
Beachtet: Das P vor der Klammer () steht für Wahrscheinlichkeit, das P in der Klammer (P) ist die Eigenschaft, dass eine Person infiziert ist.
b) 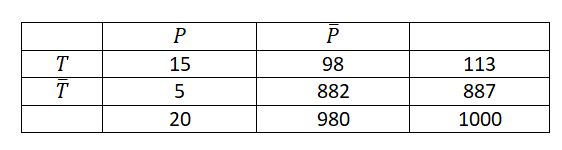
c) Tasso hat nun die Eigenschaft T. Gesucht ist 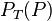 , d.h. man weiß, dass Tasso einen positiven Test hat und gesucht ist die Wahrscheinlichkeit, dass er tatsächlich auch infiziert ist.
, d.h. man weiß, dass Tasso einen positiven Test hat und gesucht ist die Wahrscheinlichkeit, dass er tatsächlich auch infiziert ist.
Mit der Merkformel muss man 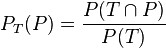 bestimmen.
bestimmen.
Aus der Vierfeldertafel liest man ab 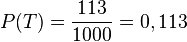 und
und 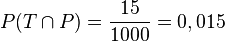 , also ist
, also ist 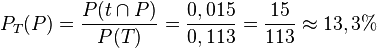 .
.
d)Für Theo gilt: Theo hat die Eigenschaft 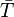 . Gesucht ist
. Gesucht ist 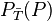 .
.
Es ist mit der Merkformel 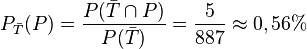 .
.
e) Nun hat man kein Baumdiagramm und auch keine Vierfeldertafel.
Tanja hat die Eigenschaft T und gesucht ist 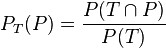
Natürlich kann man leicht auch ein neues Baumdiagramm und eine neue Vierfeldertafel anfertigen:
Die Wahrscheinlichkeiten des Tests haben sich nicht geändert.
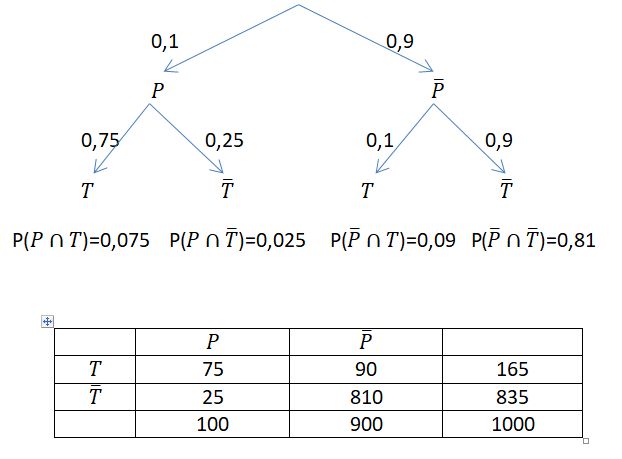
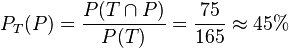
Aufgaben
80/4 Es werden hier nur die mathematischen Lösungen vorgestellt.
b) 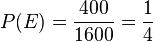 ,
, 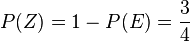
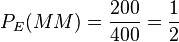 ,
, 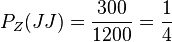
c) 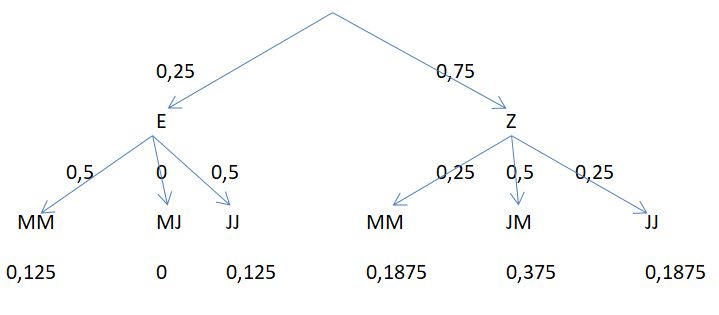
d) 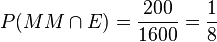
e) rosa gekleidet bedeutet wohl, dass es zwei Mädchen sind. Daher 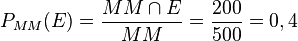 und
und 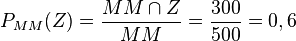 .
.
80/5 a) p=0,15, b) p=0,09, c) p=0,24
80/6 Das Baumdiagramm schaut so aus:
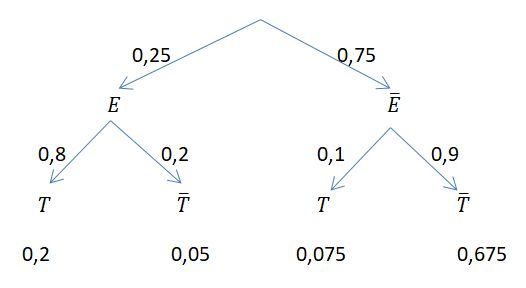
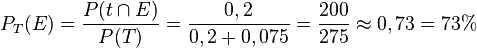
80/7 a) M bezeichnet Marschmusik
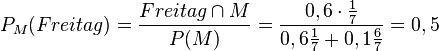
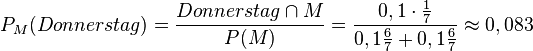
81/9
Werden z.B. 1000 Schrauben produziert, dann sind 400 Schrauben von Maschine 1 und 600 Schrauben von Maschine 2. 2,5% von den 400 Schrauben der Maschine 1 sind unbrauchbar, das sind 10 Stück. Da von 1000 Schrauben 5% unbrauchbar sind, das sind 50 Stück sind nun 10 Schrauben von Maschine 1 und 40 Schrauben von Maschine 2 unbrauchbar.
Maschine 2 produziert 600 schrauben davon sind 40 Schrauben unbrauchbar, das ist ein Anteil 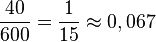
81/10

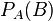 geschrieben. Der Index A gibt an, dass das Ereignis B unter der Bedingung, dass A eingetreten ist, eintritt.
geschrieben. Der Index A gibt an, dass das Ereignis B unter der Bedingung, dass A eingetreten ist, eintritt.
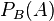 erhält man aus
erhält man aus
