M11 Aufgaben zum Wahrscheinlichkeitsbegriff
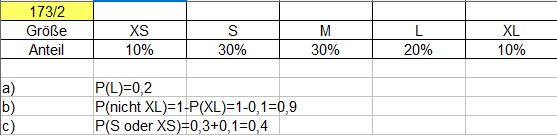
Buch S. 173 / 2
Buch S. 173 / 4
Da spätestens alle Glühfäden bei Erreichen der Temperatur T4 durchgebrannt sind, ist P(T1) + P(T2) + P(T3) + P(T4) = 0,05 + 0,1 + P(T3) + 0,25 = 1 und P(T3)=0,6.
a) Die zweite Teststufe überstehen P(T3 oder T4 = P(T3) + P(T4) = 0,6 + 0,25 = 0,85.
Oder P(T3 oder T4 = 1 - P(T1) - P(T2) = 1 - 0,05 - 0,1 = 0,85.
Buch S. 173 / 5
Die drei Ereignisse A, B und C ergeben zusammen den Ergebnisraum 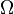 und sind paarweise unvereinbar.
und sind paarweise unvereinbar.
Es ist 1 = P(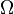 = P(A) + P(B) + P(C) = 3·P(C) + 3·P(C) + P(C) = 7·P(C), also ist
= P(A) + P(B) + P(C) = 3·P(C) + 3·P(C) + P(C) = 7·P(C), also ist 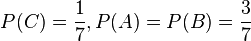
Buch S. 173 / 6
n = 3: 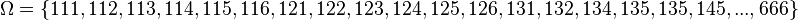 und
und 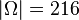
a) Höchstens eine 4 wird geworfen, wenn nur einmal eine 4 dabei ist, also hat man alle Ergebnisse ohne 4, das sind 5·5·5 = 125 Ergebnisse. Die Ergebnisse mit einer 4 bedeutet, dass an einer Stelle 4 steht, die anderen zwei Stellen sind keine 4, also hat man 3·1·5 = 15 und insgesamt 140 mögliche Ergebnisse.
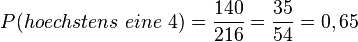
b) Mindestens eine 4 bedeutet, dass bei allen Ergebnissen kein Ergebnis ohne 4 vorkommt. Man hat 125 Ergebnisse ohne 4 (siehe a)), also gibt es 216 - 125 = 91 Ergebnisse mit mindestens einer 4.
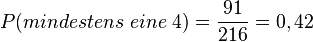
Die 91 Ergebnisse erhält man auch durch diese Überlegung: 444 ist 1 Ergebnis, zweimal 4 hat man bei 3·5 = 15 Ergebnissen (441, 442, 443, 445, 446 und die "nicht 4 Ziffer" kann an einer der drei Stellen stehen), einmal 4 hat man bei 3·5·5 = 75 Ergebnissen (4xy mit x,y ist eine der 5 anderen Ziffern und die 4 kann an einer der drei STellen stehen).
Für n beliebig kann man die analoge Überlegung anstellen: 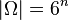
a) 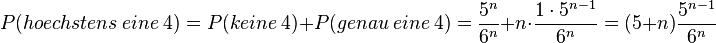
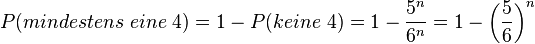
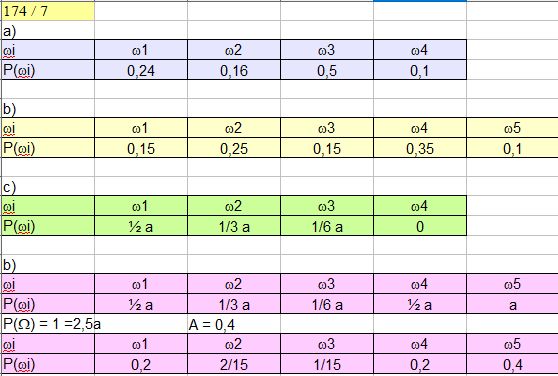
Buch S. 174 / 7
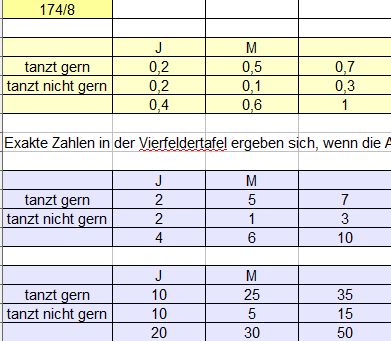
Buch S. 174 / 8