M11 Vektoren
Aus der Physik kennt man Größen wie Geschwindigkeit, Impuls, Kraft, die nicht nur einen Betrag sondern auch eine Richtung haben. Die Richtung wird durch einen Pfeil angegeben. Je Größer die Geschwindigkeit, der Impuls, die Kraft ist desto länger ist der Pfeil.
In der Mathematik kennt man Pfeile oder Vektoren von einer Verschiebung. In diesem Video
wird erkärt wie man eine Verschiebung im R2 mit Hilfe eines Vektors beschreibt.
Dieses Vorgehen übertragen wir auf unseren Raum R3. Stellt man Betrachtungen in der Zeichenebene R2 an, so setzt man die dritte Koordinate x3 einfach 0.
|
Merke:
Ein Vektor ist die Menge aller gleich langen, parallelen und gleichgerichteten Pfeile. Jeder Pfeil ist ein Repräsentant des Vektors. Jeder Repräsentant legt den Vektor fest. In einem Koordinatensystem legt man einen Vektor
Für Vektoren verwendet man eine Spaltenschreibweise Der Pfeil Sind die Pfeile zweier Vektoren Ein Vektor der Länge 0 wird mit |
Beispiele
1. Der Vektor 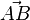 mit A(4;3;1) und B(-1;6;0) ist
mit A(4;3;1) und B(-1;6;0) ist 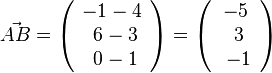 .
.
Sein Gegenvektor 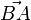 ist dann
ist dann 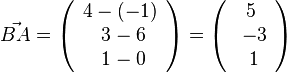 .
.
Der Ortsvektor  vom Ursprung zu A ist
vom Ursprung zu A ist 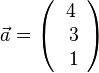 , der Ortsvektor
, der Ortsvektor 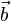 ist
ist 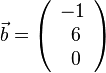 .
.
2. Die Pfeile 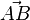 und
und 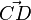 gehören zum selben Vektor
gehören zum selben Vektor 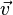 .
.
Gegeben sind A(2;3;4), B(4;7;1) und C(1;5;6). Welche Koordinaten hat D?
Es ist 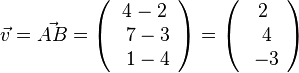
Andererseits ist 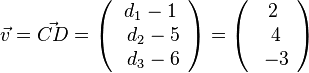 . Durch Vergleich der Koordinaten
. Durch Vergleich der Koordinaten 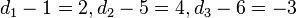 erhält man
erhält man 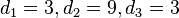 , also D(3;9;3).
, also D(3;9;3).
|
Merke:
Der Betrag Hinweis: Die Länge eines Pfeils des Vektors ist die Länge der Diagonale eines Quaders mit den Koordinaten als Länge, Breite und Höhe. |
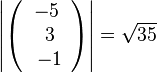 , b)
, b) 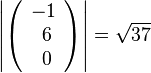 , c)
, c) 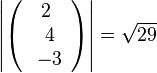 , d)
, d) 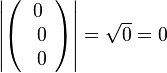 , e)
, e) 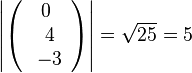

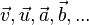 bezeichnet.
bezeichnet.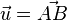 .
.
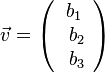 oder
oder 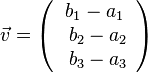 .
. 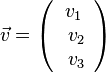 und der Vektor
und der Vektor 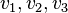 heißen Koordinaten des Vektors
heißen Koordinaten des Vektors 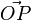 vom Ursprung O des Koordinatensystems zum Punkt P(p1;p2;p3) heißt Ortsvektor
vom Ursprung O des Koordinatensystems zum Punkt P(p1;p2;p3) heißt Ortsvektor 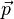 des Punktes P. Es ist
des Punktes P. Es ist 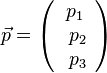 . Der Punkt P und sein Ortsvektor
. Der Punkt P und sein Ortsvektor 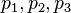 .
.
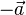 bezeichnet.
bezeichnet.
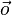 und heißt Nullvektor. Es ist
und heißt Nullvektor. Es ist 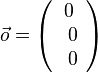 .
.
 des Vektors
des Vektors 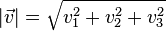 .
.
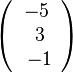 b)
b) 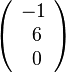 c)
c) 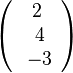 d)
d) 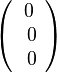 e)
e) 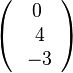
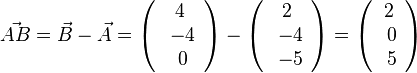
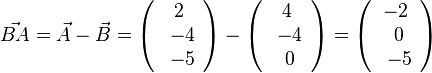
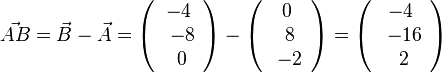
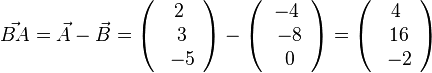
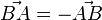
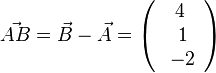 , also
, also 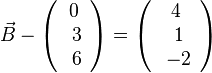 oder
oder 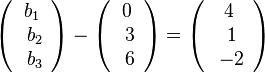 liefert
liefert 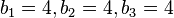 .
.
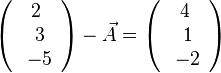 oder
oder 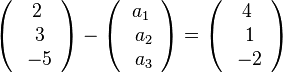 liefert
liefert 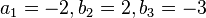 .
.
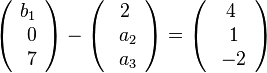 liefert
liefert 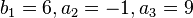
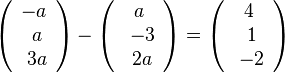 liefert
liefert 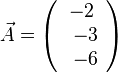 und
und 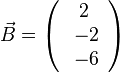
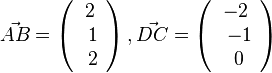
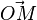 mit Startpunkt O der Ortsvektor
mit Startpunkt O der Ortsvektor 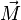 .
.
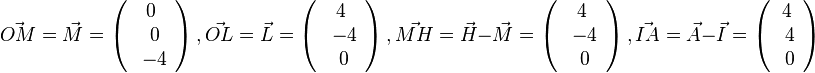
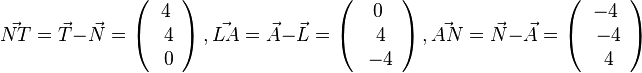
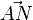 geht man von A aus -4 in x1-Richtung und kommt zur x3-Achse, dann geht man um -4 in x2-Richtung, dann ist man unterhalb von N und muss noch um 4 in x3-Richtung und ist dann in N. Die Reihenfolge wie man geht ist beliebig. Man kommt immer zu N.
geht man von A aus -4 in x1-Richtung und kommt zur x3-Achse, dann geht man um -4 in x2-Richtung, dann ist man unterhalb von N und muss noch um 4 in x3-Richtung und ist dann in N. Die Reihenfolge wie man geht ist beliebig. Man kommt immer zu N.