M11 Vektorprodukt bei der Volumenberechnung
| Kalkspat hat eine besondere Form. | 250px | 250px | 250px Diesen Effekt nennt man Doppelbrechung |
Der Körper
wird deshalb auch als Spat bezeichnet. Eigentlich heißt er Parallelepiped. Das ist Spat doch einfacher zu merken. Man kann sich vorstellen, dass ein Spat entsteht, wenn man einen Quader nach rechts und nach hinten deformiert.
Wie einen Quader kann man einen Spat durch Vektoren erzeugen.
Das Spatvolumen ist nun nach dem Prinzip von Cavalieri V = Gh, wobei G der Flächeninhalt der Grundfläche ist und h die Höhe des Spats. Den Flächeninhalt der Grundfläche bekommt man mit dem Vektorprodukt 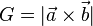 . Man weiß auch, dass das Vektorprodukt
. Man weiß auch, dass das Vektorprodukt 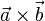 ein Vektor ist, der senkrecht zur den Vektoren
ein Vektor ist, der senkrecht zur den Vektoren  und
und 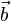 steht.
steht.
Die Richtung der Höhe ist dieselbe wie die Richtung des Vektors 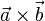 , beide stehen senkrecht zur Grundfläche.
, beide stehen senkrecht zur Grundfläche.
Aus dem Bild sieht man, dass 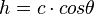 ist (,wenn
ist (,wenn 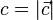 ist).
ist).
Es ist also 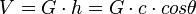 .
.
Ersetzt man nun G durch 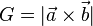 , dann ist
, dann ist 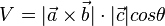 und nach der Definition des Skalarprodukts
und nach der Definition des Skalarprodukts 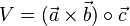 . Da das Skalarprodukt auch negativ sein kann, nimmt man für das Volumen den Betrag, also
. Da das Skalarprodukt auch negativ sein kann, nimmt man für das Volumen den Betrag, also 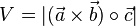 .
.
|
Merke:
Das Produkt Das Volumen des Spats, der von den Vektoren |
a) ![(\vec a \times \vec b)\circ \vec c = \left [\left ( \begin{array}{c} 2 \\\ 8 \\\ 0 \end{array}\right)\times \left ( \begin{array}{c} -4 \\\ 2 \\\ 1 \end{array}\right) \right ] \circ \left ( \begin{array}{c} -4 \\\ 2 \\\ 6 \end{array}\right) = \left ( \begin{array}{c} 8 \\\ -2 \\\ 36 \end{array}\right) \circ \left ( \begin{array}{c} -4 \\\ 2 \\\ 6 \end{array}\right)=-32-4+216=180](/images/math/3/7/9/379bfda881bada0ae22176b0465b0dde.png)
b) ![(\vec b \times \vec c)\circ \vec a=\left [ \left ( \begin{array}{c} -4 \\\ 2 \\\ 1 \end{array}\right) \times \left ( \begin{array}{c} -4 \\\ 2 \\\ 6 \end{array}\right) \right ] \circ \left ( \begin{array}{c} 2 \\\ 8 \\\ 0 \end{array}\right)= \left ( \begin{array}{c} 10 \\\ 20 \\\ 0 \end{array}\right) \circ \left ( \begin{array}{c} 2 \\\ 8 \\\ 0 \end{array}\right) =20+160=180](/images/math/d/6/6/d66ce813bd0461f92d9e1a12f897b86b.png)
![(\vec c \times \vec a) \circ \vec b=\left [ \left ( \begin{array}{c} -4 \\\ 2 \\\ 6 \end{array}\right) \times \left ( \begin{array}{c} 2 \\\ 8 \\\ 0 \end{array}\right) \right ] \circ \left ( \begin{array}{c} -4 \\\ 2 \\\ 1 \end{array}\right)= \left ( \begin{array}{c} -48 \\\ 12 \\\ -36 \end{array}\right) \circ \left ( \begin{array}{c} -4 \\\ 2 \\\ 1 \end{array}\right) = 192+24-36=180](/images/math/6/3/b/63b94b60dd8b5eb57dd38359ba5f29a6.png)
30px Merke
Wichtig ist, dass man einen Eckpunkt nimmt. Es ist egal welchen. Für die Berechnung des Volumens nimmt man die drei Vektoren, die von diesem Eckpunkt weggehen. Für die Berechnung des Volumens ist auch die Reihenfolge wie man die Vektoren in die Gleichung für das Spatvolumen einsetzt, egal. Da man am Ende den Betrag nimmt, kommt stets ein positives Volumen heraus. |
![V=|(\vec a \times \vec b) \circ \vec c|=\left | \left [ \left ( \begin{array}{c} 1 \\\ 0 \\\ 2 \end{array}\right) \times \left ( \begin{array}{c} -2 \\\ 3 \\\ 1 \end{array}\right ) \right ] \circ \left ( \begin{array}{c} 0 \\\ 1 \\\ 4 \end{array}\right) \right |= \left | \left ( \begin{array}{c} -6 \\\ -5 \\\ 3 \end{array}\right) \circ \left ( \begin{array}{c} 0 \\\ 1 \\\ 4 \end{array}\right) \right | = |-5+12|=7](/images/math/6/a/7/6a717fc3976c19eb9f9ea714c26986dd.png)
Mit diesen Überlegungen kann man auch eine Formel zur Berechnung von Pyramidenvolumina erhalten.
|
Merke:
Das Volumen einer Pyramide, die ein
|
Anmerkung: In der Mittelstufe hat man gelernt, dass das Volumen eines Quaders oder eines geraden Körpers 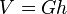 ist. Das Volumen eines Körpers mit Spitze wie Pyramide, Kegel ist stets
ist. Das Volumen eines Körpers mit Spitze wie Pyramide, Kegel ist stets 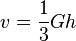 . Daher
. Daher  in der Pyramidenformel.
in der Pyramidenformel.
Da der Flächeninhalt mittels dem Vektorprodukt berechnet wird, ist der Flächeninhalt eines Parallelogramms 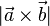 und der Flächeninhalt eines Dreiecks
und der Flächeninhalt eines Dreiecks 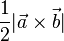 . Daher
. Daher 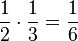 in der Formel für den Tetraeder.
in der Formel für den Tetraeder.
119/5
Die vier Punkte legen einen Tetraeder fest.
a) Elementargeometrisch heißt man verwendet die Formal aus der Mittelstufe 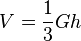 . G ist der Flächeninhalt eines rechtwinkligen Dreiecks mit den Katheten 3 und 4. Die Höhe der Pyramide ist 2. Also ist
. G ist der Flächeninhalt eines rechtwinkligen Dreiecks mit den Katheten 3 und 4. Die Höhe der Pyramide ist 2. Also ist 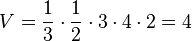 .
.
Zu bemerken ist hier, dass man nicht das Dreieck ABC als Grundfläche nehmen muss. Hier verwendet man als Grundfläche das Dreieck ABC und [DC] ist dann die Höhe der Pyramide!
b) Als Eckpunkt für die Berechnung des Volumens nimmt man z.B. A und die Vektoren 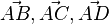 . Es ist
. Es ist 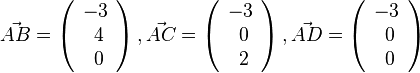
![V= \frac{1}{6}|(\vec {AB} \times \vec {AC}) \circ \vec {AD}|=\frac{1}{6}\left | \left [ \left ( \begin{array}{c} -3 \\\ 4 \\\ 0 \end{array}\right) \times \left ( \begin{array}{c} -3 \\\ 0 \\\ 2 \end{array}\right ) \right ] \circ \left ( \begin{array}{c} -3 \\\ 0 \\\ 0 \end{array}\right) \right |= \frac{1}{6}\left | \left ( \begin{array}{c} 8 \\\ 6 \\\ -12 \end{array}\right) \circ \left ( \begin{array}{c} -3 \\\ 0 \\\ 0 \end{array}\right) \right | =\frac{1}{6} |-24|=4](/images/math/3/e/b/3eb423963b2652bd0d2b8511ab7bceea.png)
119/6
Die vier Punkte A, B, C und D legen ein Quadrat fest. Es ist zu zeigen, dass die Vektoren 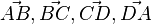 ein Parallelogramm bilden,
ein Parallelogramm bilden, 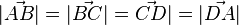 ist und ein 90°-Winkel da ist.
ist und ein 90°-Winkel da ist.
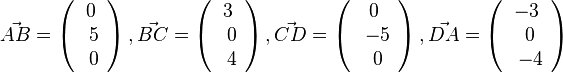 .
.
Man sieht 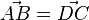 und
und 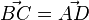 und
und 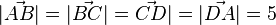 ist. Außerdem ist
ist. Außerdem ist 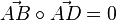 , also ist bei A ein 90°-Winkel.
, also ist bei A ein 90°-Winkel.
Man soll das Volumen auf 2 Arten berechnen.
1. mit der Volumenformel
Als Eckpunkt nimmt man z.B. A und damit die Vektoren 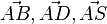 . Es ist
. Es ist 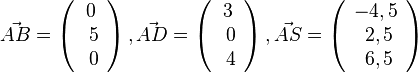 . Damit berechnet man
. Damit berechnet man
![V=\frac{1}{3}|(\vec {AB} \times \vec {AD}) \circ \vec {AS}| = \frac{1}{3} \left | \left [ \left ( \begin{array}{c} 0 \\\ 5\\\ 0 \end{array}\right) \times \left ( \begin{array}{c} 3 \\\ 0 \\\ 4 \end{array}\right) \right ] \circ \left ( \begin{array}{c} -4,5 \\ 2,5 \\\ 6,5 \end{array}\right) \right | = \frac{1}{3} \left | \left ( \begin{array}{c} 20 \\\ 0 \\\ -15 \end{array}\right) \circ \left ( \begin{array}{c} -4,5 \\\ 2,5 \\\ 6,5 \end{array}\right) \right |= \frac{1}{3}\cdot |-90-97,5|=62,5](/images/math/3/a/8/3a82f1b280a25b76f056c6c207574ec2.png)
2. elemtentargeometrisch
Die Grundfläche ist ein Quadrat mit Seitenlänge 5, der Flächeninhalt G = 25.
Die Seitenvektor 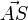 hat die Länge
hat die Länge 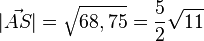 Die Höhe ist eine Kathete im rechtwinkligen Dreieck AFS, wenn F der Mittelpunkt der Diagonalen [AC] ist. Die Diagonale hat die Länge
Die Höhe ist eine Kathete im rechtwinkligen Dreieck AFS, wenn F der Mittelpunkt der Diagonalen [AC] ist. Die Diagonale hat die Länge 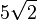 , also ist die halbe Diagonale
, also ist die halbe Diagonale 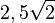 lang und es ist dann
lang und es ist dann 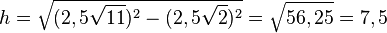
(Hier hätte man eigentlich noch nachweisen müssen, dass alle 4 Kanten gleich lang sind und damit die Pyramide gerade ist.)
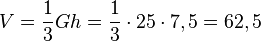 .
.Zum Abschluss die beiden Pyramiden der Aufgabe 3:

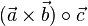 heißt Spatprodukt.
heißt Spatprodukt.
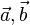 und
und 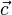 aufgespannt wird,ist
aufgespannt wird,ist 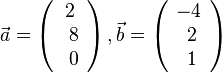 und
und 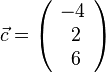 .
.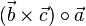
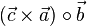
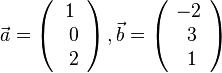 und
und 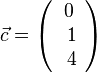 aufgespannt ist.
aufgespannt ist.
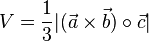 (ägyptische Pyramide).
(ägyptische Pyramide).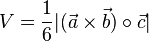 (Tetraeder).
(Tetraeder).

