M11 Verknüpfte Ereignisse
|
Merke:
Der Ergebnisraum Das Ereignis E enthält alle für E günstigen Ergebnisse. Die einelementigen Ereignisse Ein Ereignis, das alle Ergebnisse des Zufallsexperiments enthält heißt sicheres Ereignis. Ein Ereignis, das bei dem Zufallsexperiment nicht eintreten kann, das also kein Ergebnis enthält ist ein unmögliches Ereignis. Das Ereignis Es ist |
| Sprechweisen | Schreibweisen |
|---|---|
| Gegenereignis zu A, Nicht A | 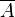 |
| Ereignis A und Ereignis B, Beide Ereinisse | 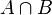 |
| Ereignis A oder Ereignis B | 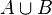 |
| Keines der beiden Ereignisse, Weder A noch B | 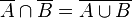 |
| Höchstens eines der beiden Ereignisse, Nicht beide Ereignisse | 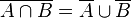 |
| Genau eines der beiden Ereignisse, Entweder A oder B | 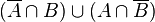 |
Im Buch auf S. 177 finden Sie zu den verknüpften Ereignissen schöne Veranschaulichungen.
178/1
a) 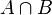
b) 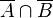
c) 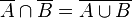
d) 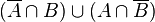
179/2 P(mindestens ein Würfel hat gerade Augenzahl)= 1 - P(kein Würfel hat gerade Augenzahl) = 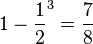
179/3
a) 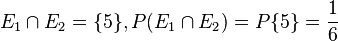
b) 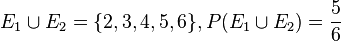
c) 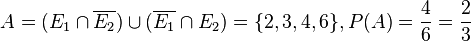
d) 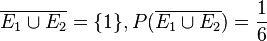
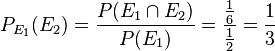
179/4 a) Alle drei Ereignisse treten ein, also hat "Britta Gold", "Lisbeth Silvbr" und "Natalie Bronze".
b) Britta hat nicht Gold, da Natalie Bronze hat, hat "Lisbeth Gold", "Britta Silber" und "Natalie Bronze".
c) Britta hat Gold und Lisbeth hat Bronze, also hat Natalie Silber.
d) Lisbeth hat Bronze, Britta Silber und Natalie Gold.
e) Es ist 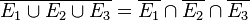 , also hat Lisbeth Silber, Natalie Gold und Britta Bronze.
, also hat Lisbeth Silber, Natalie Gold und Britta Bronze.
f) Britta hat Gold oder (Lisbeth und Natalie haben Silber und Gold, Britta hat Bronze).
179/6a) 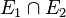 bedeutet, dass Löwe 1 und Löwe 2 in ihren Käfigen sind.
bedeutet, dass Löwe 1 und Löwe 2 in ihren Käfigen sind.
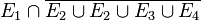 bedeutet, dass kein Löwe in seinem Käfig ist.
bedeutet, dass kein Löwe in seinem Käfig ist.
b) 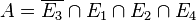
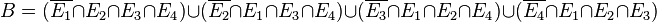
179/7
a) Jeder Schüler tanzt mit seiner Freunding.
b) Ein Schüler tanzt mit seiner Freundin.
c) Kein Schüler tanzt mit seiner Freundin.
179/5 Man hat 3 Ziffern 2, 3, und 6 mit den Wahrscheinlichkeiten 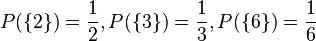 . Es gibt
. Es gibt 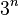 verschiedene Ergebnisse.
verschiedene Ergebnisse.
a) 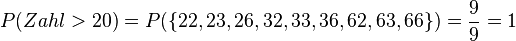 , ein sicheres Ereignis.
, ein sicheres Ereignis.
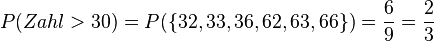
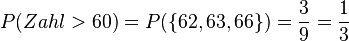 .
.
 , ein unmögliches Ereignis.
, ein unmögliches Ereignis.
b) n = 4, 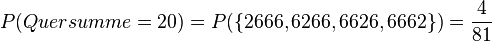
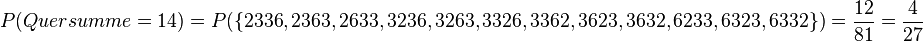
c) 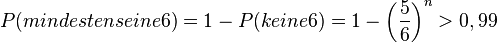
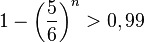
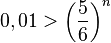
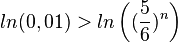
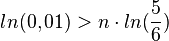
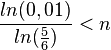 , da man die Ungleichung durch eine negative Zahl geteilt hat!
, da man die Ungleichung durch eine negative Zahl geteilt hat!
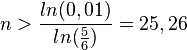 , also muss man das Glücksrad mindestens 26 mal drehen.
, also muss man das Glücksrad mindestens 26 mal drehen.
180/9 a) 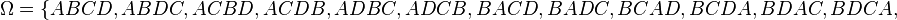
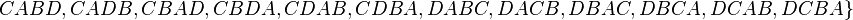 und
und 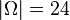 .
.
Man hätte auch einfach 4! = 24 rechnen können!
b) 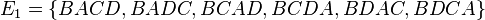 ,
,
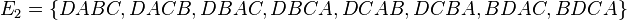
c) 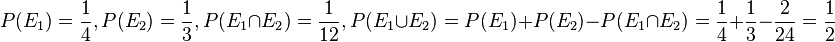
d) 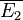 ist das Ereignis, dass Anton und Cecilia nicht beide nach Doreen geprüft werden.
ist das Ereignis, dass Anton und Cecilia nicht beide nach Doreen geprüft werden.
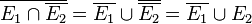 ist das Ereignis, dass Bertram nicht als erster geprüft wird oder Anton und Cecilia beide nach Doreen geprüft werden.
ist das Ereignis, dass Bertram nicht als erster geprüft wird oder Anton und Cecilia beide nach Doreen geprüft werden.
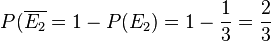
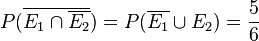
e) 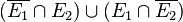 , das ist ein ausschließendes "oder", d.h. es dürfen nicht beide Ereignisse gemeinsam eintreten.
, das ist ein ausschließendes "oder", d.h. es dürfen nicht beide Ereignisse gemeinsam eintreten.
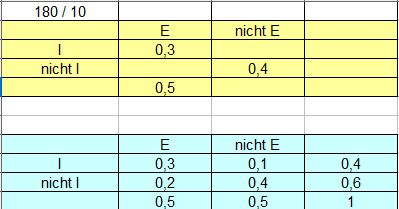
180/10 Man legt am besten eine Vierfeldertafel an, ergänzt die fehlenden Einträge und berechnet dann die bedingte Wahrscheinlichkeit.
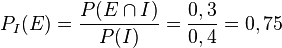

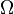 ist die Menge aller möglichen Ergebnisse. Es ist
ist die Menge aller möglichen Ergebnisse. Es ist 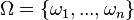 .
.
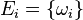 heißen Elementarereignisse.
heißen Elementarereignisse.
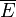 enthält alle für E ungünstigen Ergebnisse, also alle Ergebnisse, die nicht in E sind und heißt Gegenereignis von E.
enthält alle für E ungünstigen Ergebnisse, also alle Ergebnisse, die nicht in E sind und heißt Gegenereignis von E.
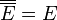 .
.

