M11 dreidimensionales Koordinatensystem
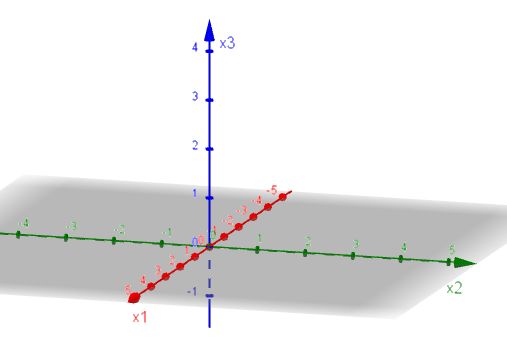
Wir erweitern unser zweidimensionales xy-Koordinatensystem durch eine dritte z-Koordinate.
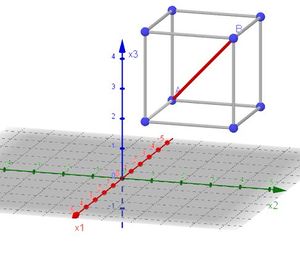
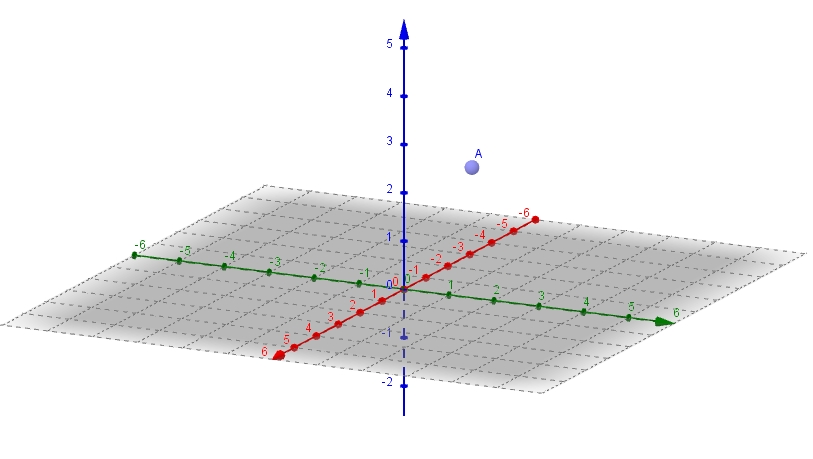
In Geogebra klicken Sie das Fenster "Grafik" weg und wählen im Menü "Ansicht" die Auswahl "3D Grafik" aus. Geben Sie unten in der Eingabezeile A=(1,2,3) ein. Nun wird der Punkt A eingezeichnet. Sie können nun durch Drehen die Lage des Koordinatensystems ändern und erkennen, dass die rote Achse die x-Achse, die grüne Achse die y-Achse und die blaue Achse die z-Achse ist. Es wird nun ein räumliches Koordinatensystem angezeigt.
Um mit unserem Buch konform zu sein, nennen wir die x-Koordinate nun x1-Koordinate, die y-Koordinate nun x2-Koordinate und die z-Koordinate nun x3-Koordinate.
Für unseren Punkt A(1;2;3) bedeutet dies, dass x1=1, x2=2 und x3=3 ist.
In GeoGebra ist die x1-Achse rot, die x2-Achse grün und die x3-Achse blau.
Die x1-Koordinate des Punktes P(2;4;5) ist (!4) (2) (!5)
Die x3-Koordinate des Punktes P(-1;24;5) ist (!-1) (5) (!24)
Die x2-Koordinate des Punktes P(2;-4;-5) ist (!2) (-4) (!-5)
Beim Punkt P(-3;4;12) ist 12 welche Koordinate? (!x1) (!x2) (x3)
Bei P(-1;24;5) ist 24 welche Koordinate? (!x1) (x2) (!x3)
Bei P(-3;21;2) ist -3 welche Koordinate? (x1) (!x2) (!x3)
30px Merke
Wir vereinbaren zum Zeichnen eines dreidimensionalen Koordinatensystems die x2x3-Ebene als Zeichenebene (Heftebene). Die x1- und x2-Achse werden normalerweise jeweils nach 2 Kästchen vom Ursprung mit 1 bezeichnet. 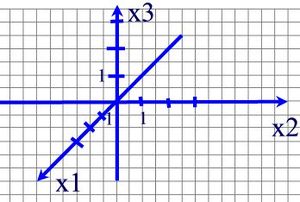 |
a) R(2;-2;0), H(2;2;0), A(-2;2;0), E(-2;-2;0), T(2;-2;4), I(2;2;4), C(-2;2;4), U(-2;-2;4), S(0;0;7)
Das Turmvolumen ist 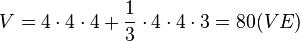
b) S(4;-4;0), T(4;4;0), E(0;4;0), V(0;-4;0), I(0;-4;3), N(0;4;3)
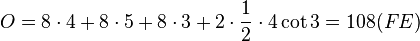
30px Merke
Der Abstand zweier Punkte P(p1;p2;p3) und Q(q1;q2;q3) ist nach dem Satz von Pythagoras 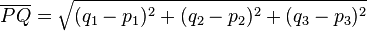 |
1. Die Strecke [OA] ist die Diagonale in einem Quader mit den Seitenlängen 1, 2 und 3.
Es ist 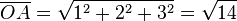
2. Die Strecke [AB] ist die Diagonale in einem Quader mit den Seitenlängen, 3, 3 und 3
Es ist 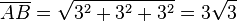
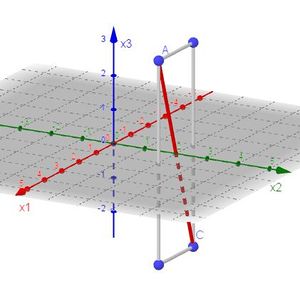
3. Die Strecke [AC] ist die Diagonale in einem Quader mit den Seitenlängen 2, 0 und 6, also einem Rechteck.
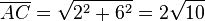
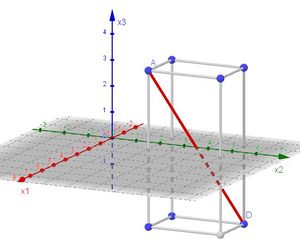
4. Die Strecke [AD] ist die Diagonale in einem Quader mit den Seitenlängen 2, 3 und 6, also einem Rechteck.
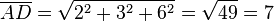
Um weiter mit unserem Buch konform zu sein, vereinbaren wir, dass wir ein dreidimensionales Koordinagensystem so zeichnen, dass die x1-Achse schräg nach vorne zeigt, die x2-Achse nach rechts und die x3-Achse nach oben.
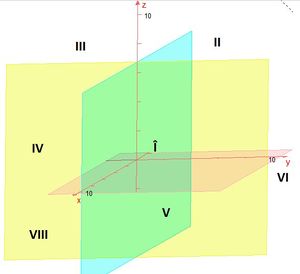
Die Koordinatenebenen zerlegen den Raum in acht Teile, sogenannte Oktanten.
|
V. Oktant: x1 > 0, x2 > 0, x3 > < 0 |
Durch die Achsen werden drei Ebenen festgelegt:
- x1x2-Ebene (rot),
- x1x3-Ebene (blau),
- x2x3-Ebene (gelb).
In der Zeichenebene werden durch das xy-Diagramm die Koordinaten von Punkten festgelegt. Die Zeichenebene ist eine Punktmenge von Punkten P(x;y), wobei die Ebeme durch R2={(x;y)|x, y sind reelle Zahlen} beschrieben wird.
Dies übertragen wir auf unseren neuen Raum, den Anschauungsraum. Jeder Punkt P(x1;x2;x3) ist durch seine drei Koordinaten x1, x2 und x3 festgelegt. Die Punktmenge aller Punkte des Raumes ist dann R3={(x1;x2;x3)|x1, x2, x3 sind reelle Zahlen}.
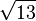 zum Ursprung.
zum Ursprung.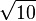 zum Ursprung.
zum Ursprung.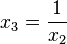 . Dies ist in der x2x3-Ebene eine Hyperbel.
. Dies ist in der x2x3-Ebene eine Hyperbel.
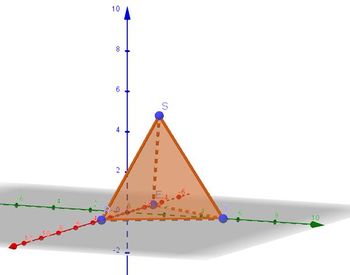
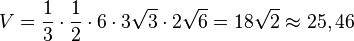
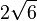 , da die Punkte R I und S in der x1x2-Ebene liegen und der Abstand von S von der x1x2-Ebene ist seine x3-Koordinate.
, da die Punkte R I und S in der x1x2-Ebene liegen und der Abstand von S von der x1x2-Ebene ist seine x3-Koordinate.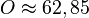
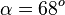 ,
,