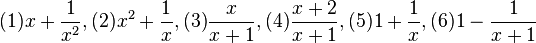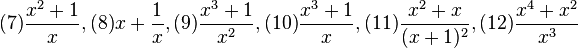M8-Rechnen mit Bruchtermen
Wir haben uns mit gebrochen-rationalen Funktionen beschäftigt. Terme dieser Funktionen sind im Normalfall Bruchterme. In der 6. Klasse hast du gelernt mit Brüchen (Zahlen) zu rechnen. Da kamen in Zähler und Nenner des Bruches nur Zahlen vor. Bei den gebrochen-rationalen Funktionen steht auch die Variable im Nenner, eventuell auch im Zähler. Daher müssen wir auch mit Brüchen arbeiten können, wenn Variable oder Parameter in Zähler und/oder Nenner vorkommen.
Zur Festigung deiner Grundkenntnisse wollen wir zuerst einiges vom Stoff der 6. und 7. Klasse wiederholen.
Erweitern: Der erste Bruch wird mit x, der zweite Bruch mit 5 erweitert, d.h. Zähler und Nenner werden mit x bzw. 5 multipliziert. Wenn Zähler oder Nenner eine Summe oder Differenz sind, dann setze sie in Klammern und multipliziere die Klammer!
Kürzen: Bei den Termen in Zähler und Nenner kann man jeweils x ausklammern. Der Rest bleibt kommt in Klammern. Stehen in Zähler und Nenner gleiche Faktoren, so kann man diese kürzen.
Addition: Brüche muss man beim Addieren oder Subtrahieren gleichnamig machen. Dies passiert hier, indem man die beiden Nenner multipliziert. Das ist dann der Hauptnenner. Haben beide Brüchen denselben Nenner, dann addiert bzw. subtrahiert man ihre Zähler und fasst zusammen.
Multiplikation: Zwei Brüche werden multipliziert, indem man ihre Zähler mulitpliziert und ihre Nenner multiziert.
Dann vereinfacht man den Zähler. Den Nenner lässt man so stehen, man multipliziert nicht aus. Man sieht dann leichter ob man noch kürzen kann.
30px Merke
Mit Bruchtermen kann man wie mit Brüchen rechnen. Beachte: Aus Summen und Differenzen kürzen wir nicht! |
|
Merke:
1. Erweitern und Kürzen 2. Addition und Subtraktion 3. Multiplikation und Division |
Beipiele:
1. Erweitern: 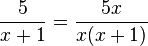
Der Bruch wurde mit x erweitert, d.h. Zähler und Nenner werden mit x multipliziert. Beachte dabei, dass du den Nenner x+1 in Klammern setzt, denn der ganze Nenner wird mit x multipliziert.
Kürzen:
Der Bruch wurde mit x gekürzt.Im Nenner steht ein Produkt, dessen 1. Faktor x ist. Man darf kürzen, wenn in Zähler und Nenner Produkte stehen.
-
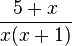 kann man nicht kürzen, da im Zähler eine Summe steht, die sich nicht durch Ausklammern in ein Produkt verwandeln lässt.
kann man nicht kürzen, da im Zähler eine Summe steht, die sich nicht durch Ausklammern in ein Produkt verwandeln lässt.
-
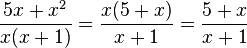
Hier kann man im Zähler x ausklammern, dann stehen in Zähler und Nenner Produkte, die jeweils x als Faktor haben. Dieses x darf man nun kürzen. Der verbleibende Bruch ist nicht weiter kürzbar! In Zähler und Nenner kommt zwar jeweils x vor, aber x steht in einer Summe und aus Summen kürzt man nicht!
- Und wenn man im letzten Beispiel beim Ergebnis noch x ausklammert?
Man kann natürlich im Bruch 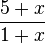 x ausklammern. Man erhält dann diesen Bruch:
x ausklammern. Man erhält dann diesen Bruch:
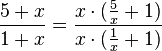 und nun kann man, da x in Zähler und Nenner jeweils in einem Produkt vorkommt, x kürzen, aber das Ergebnis
und nun kann man, da x in Zähler und Nenner jeweils in einem Produkt vorkommt, x kürzen, aber das Ergebnis 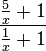 ist "kein schönes Ergebnis", da lässt man lieber
ist "kein schönes Ergebnis", da lässt man lieber 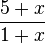 stehen und hört auf.
stehen und hört auf.
- Beim Bruch
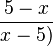 schauen Zähler und Nenner ja fast gleich aus. Wodurch unterscheiden sie sich?
schauen Zähler und Nenner ja fast gleich aus. Wodurch unterscheiden sie sich?
Man kann beim Zählerterm -1 ausklammern und hat dann 5 - x = -(-5 + x) (Distributivgesetz!) und 5 - x = -(-5 + x) = -(x - 5) (Kommutativgesetz!).
Nun steht in der Klammer derselbe Term wie im Nenner.
Der Nenner ist auf natürliche Weise ein Produkt, es ist nämlich x - 5 = 1·(x - 5). Deshalb kann man nun den gemeinsamen Faktor (x - 5) kürzen. Also 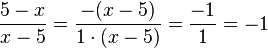
- 30px Übung
a) Darf man 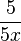 kürzen?
(ja) (!nein)
kürzen?
(ja) (!nein)
b) Darf man 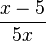 kürzen?
(!ja) (nein)
kürzen?
(!ja) (nein)
c) Darf man 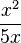 kürzen?
(ja) (!nein)
kürzen?
(ja) (!nein)
d) Darf man 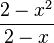 kürzen?
(!ja) (nein)
kürzen?
(!ja) (nein)
e) Darf man 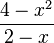 kürzen?
(ja) (!nein)
kürzen?
(ja) (!nein)
f) Darf man 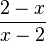 kürzen?
(ja) (!nein)
kürzen?
(ja) (!nein)
a) 5 ist gemeinsamer Faktor von Zähler und Nenner. Das Ergebnis ist 
b) Im Zähler steht eine Differenz aus der man "nichts" ausklammern kann. Man kann nicht kürzen.
c) x ist gemeinsamer Faktor in Zähler und Nenner. 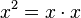 , das Ergebnis ist
, das Ergebnis ist 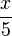
d) In Zähler und Nenner stehen Differenzen, aus denen man nichts ausklammern kann. Man kann nichts kürzen.
e) Der Term im Zähler 4 - x2 lässt sich umformen in 4 - x2 = (2-x)(2+x) und dann kann man 2-x kürzen. Das Ergebnis ist x + 2.
2. Addition und Subtraktion: 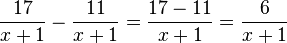
Die Brüche sind gleichnamig, dann kann man gleich die Zähler addieren bzw. subtrahieren.
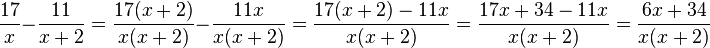
Hier muss man für die zwei Brüche erst einen gleichen Nenner finden. Dazu wird der erste Bruch wird mit x+2 (=Nenner des 2. Bruches) erweitert, der zweite Bruch mit x (=Nenner des 1. Bruches). Wenn man gleiche Nenner hat, dann kann man die Zähler addieren bzw. subtrahieren und zusammenfassen bzw. vereinfachen. Im Nenner lässt man das Produkt stehen!
3. Multiplikation: 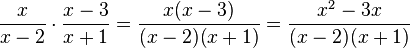
Beim Multiplizieren werden die Zähler und die Nenner jeweils miteinander multipliziert. Den Zähler vereinfacht man noch. Im Nenner lässt man das Produkt stehen.
Division: 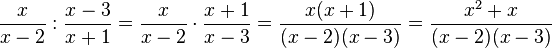
Beim zweiten Bruch wird der Kehrbruch gebildet, indem man Zähler und Nenner vertauscht. Der Zähler des Bruches wird zum Nenner des Kehrbruches, der Nenner des Bruches wird zum Zähler des Kehrbruches. Dann wird der 1. Bruch mit dem Kehrbruch des 2. Bruches multiplliziert, der Zähler vereinfacht und im Nenner bleibt das Produkt stehen.
In diesem Video wird alles nochmal zusammengefasst:
Bruchgleichungen am Ende des Videos kommen für uns erst später. Das ist dann unser nächstes Thema.
1. 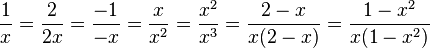
Zähler und Nenner werden jeweils mit dem Erweiterungsfaktor, der in den Aufgaben a) - f) gegeben ist multipliziert.
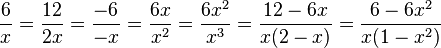
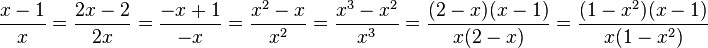
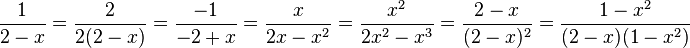
2. Den Erweiterungsfaktor erhältst du, wenn du den in eckigen Klammern angegebenen Nenner durch den Nenner des Bruches dividierst.
a) 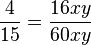 Erweiterungsfaktor 4xy
Erweiterungsfaktor 4xy
Definitionsmenge Q\{x=0; y=0}
b) 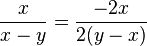 Erweiterungsfaktor -2
Erweiterungsfaktor -2
Beachte, dass x-y=-(y-x) ist!
Definitionsmenge Q\{x=y} (Der Nenner ist Null, wenn x = y ist. Also darf man diese Zahlen, wenn x = y ist, nicht einsetzen! Es muss x≠y sein!)
c) 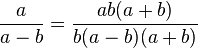 Erweiterungsfaktor b(a+b)
Erweiterungsfaktor b(a+b)
Definitionsmenge: Der Nenner ist Null, wenn b = 0 oder a = b oder a = -b ist, also Q\{(b=0; a=b; a=-b}
d) 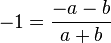 Erweiterungsfaktor a+b
Erweiterungsfaktor a+b
Hier ist der Nenner -(a+b) noch vereinfacht zu -a-b.
Definitionsmenge Q\{a≠-b}
e) 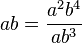 Erweiterungsfaktor ab3
Erweiterungsfaktor ab3
Definitionsmenge Q\{a=0; b=0}
f) 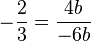 Erweiterungsfaktor 2b
Erweiterungsfaktor 2b
Das Minuszeichen kann man auch in den Nenner schreiben!
Definitionsmenge Q\{0}
g) 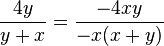 Erweiterungsfaktor -x
Erweiterungsfaktor -x
Es ist x+y=y+x (Kommutativgesetz)!
Definitionsmenge Q\{x=0; x=-y}
h) 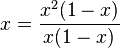 Erweiterungsfaktor x(1-x)
Erweiterungsfaktor x(1-x)
Definitionsmenge Q\{0;1}
i) 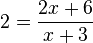 Erweiterungsfaktor x+3
Erweiterungsfaktor x+3
Definitionsmenge Q\{-3}
j) 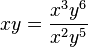 Erweiterungsfaktor x3y5
Erweiterungsfaktor x3y5
Definitionsmenge Q\{x=0; y=0}
k) 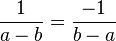 Erweiterungsfaktor -1
Erweiterungsfaktor -1
Definitionsmenge Es muss a≠b sein, also Q\{(a=b}
3. Suche gemeinsame Faktoren von Zähler und Nenner. Eventuell musst du ausklammern.
Zur Angabe der Definitionsmenge musst du den in der Aufgabe gegebenen Term betrachten.
a) In Zähler und Nenner stehen 2 und x jeweils als Faktoren.
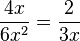 gekürzt mit 2x
gekürzt mit 2x
D = Q\{0}
b) In Zähler und Nenner stehen x-4 und x als Faktoren.
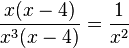 gekürzt mit x(x-4)
gekürzt mit x(x-4)
D = Q\{0;4} Beachte, dass man im gekürzten Term 4 einsetzen dürfte, für den gekürzten Term ist D = Q\{0}.
c) Stelle zuerst Zähler oder Nenner um, indem du -1 ausklammerst.
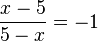 gekürzt mit 5-x
gekürzt mit 5-x
Beachte: x-5 = -(-x+5) = -(5-x)
D = Q\{5}, für den gekürzten Term ist D = Q.
d) 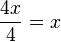 gekürzt mit 4
gekürzt mit 4
D = Q
e) 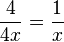 gekürzt mit 4
gekürzt mit 4
D = Q\{0}
f) 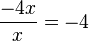 gekürzt mit x
gekürzt mit x
D = Q\{0}, für den gekürzten Term ist D = Q.
g) 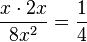 gekürzt mit 2x2
gekürzt mit 2x2
D = Q\{0}, für den gekürzten Term ist D = Q.
h) 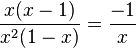 gekürzt mit x(1-x)
gekürzt mit x(1-x)
Beachte: x-1 = -(1-x)
D = Q\{0;1}, für den gekürzten Term ist D = Q\{0}.
i) 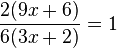 gekürzt mit 2·3·(3x+2)
gekürzt mit 2·3·(3x+2)
Im Zähler kannst du bei der Klammer 3 ausklammer 9x+6 = 3(3x+2).
Beachte: Im Nenner kann man 6 in zwei Faktoren zerlegen 6 = 2·3!
D = Q\{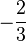 }, für den gekürzten Term ist D = Q.
}, für den gekürzten Term ist D = Q.
j) 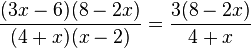 gekürzt mit x-2
gekürzt mit x-2
Im Zähler kann man beim Faktor 3x-6 die Zahl 3 ausklammern.
D = Q\{-4;2}, für den gekürzten Term ist D = Q\{-4}.
k) 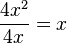 gekürzt mit 4x
gekürzt mit 4x
D = Q\{0}, für den gekürzten Term ist D = Q.
l) 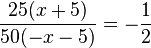 gekürzt mit 25(x+5)
gekürzt mit 25(x+5)
Im Nenner kannst du -1 ausklammern -x-5=-(x+5) oder im Zähler x+5=-(-x-5). Das - schreibt man dann vor den Bruch.
D = Q\{-5}, für den gekürzten Term ist D = Q.
m) 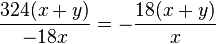 gekürzt mit 18
gekürzt mit 18
D = Q\{0}
n) 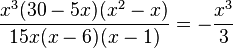 gekürzt mit 5x(x-6)(x-1)
gekürzt mit 5x(x-6)(x-1)
Beachte: Ausklammern bei 30-5x = 5(6-x) und x2-x=x(x-1)!
D = Q\{1;6}, für den gekürzten Term ist D = Q.
o) 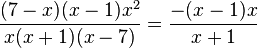 gekürzt mit x(x-7)
gekürzt mit x(x-7)
Beachte 7-x=-(x-7)
D = Q\{-1;0;7}, für den gekürzten Term ist D = Q\{-1}.
p) Im Nenner kann man 6 ausklammern. Dann sind in Zähler und Nenner jeweils 3 und x-4 Faktoren, die man kürzen kann.
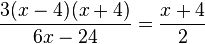 gekürzt mit 3(x-4)
gekürzt mit 3(x-4)
D = Q\{-4}, für den gekürzten Term ist D = Q.
q) 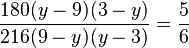 gekürzt mit 36(9-y)(y-3)
gekürzt mit 36(9-y)(y-3)
Beachte: - mal - = +
D = Q\{3;9}, für den gekürzten Term ist D = Q.
r) Klammere in Zähler und Nenner aus!
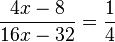 gekürzt mit 4x-8
gekürzt mit 4x-8
D = Q\{2}, für den gekürzten Term ist D = Q.
s) Klammere zuerst in Zähler und Nenner aus!
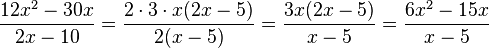 gekürzt mit 2, mehr geht nicht.
gekürzt mit 2, mehr geht nicht.
1.
Überlege dir zuerst den Hauptnenner, eventuell die Nenner miteinander multiplizieren (aber nicht ausrechnen, nur Faktor · Faktor!) und erweitere dann die Brüche mit dem jeweiligen Erweiterungsfaktor. Fasse dann die Zähler zusammen und vereinfache den gemeinsamen Zähler.
Für die Definitionsmenge musst du bei allen Summanden darauf achten, dass keine 0 im Nenner stehen darf.
a) Die Zahl 1 lässt sich als Bruch  schreiben und dann mit x erweitern. Es ist
schreiben und dann mit x erweitern. Es ist 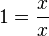 .
.
Ergebnis: 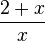
D=Q\{0}
b) Der Hauptnenner ist das Produkt der beiden Nenner 2 und x. Erweitere die beiden Brüche passend und fasse dann zusammen.
Ergebnis: 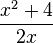
D=Q\{0}
c) Die Nenner sind gleich, also kann man gleich die Zähler subtrahieren.
Ergebnis: 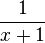
D=Q\{-1}
d) Gleiche Nenner, also Zähler addieren.
Ergebnis: 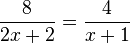
Im Ergebns kann man im Nenner 2 ausklammern und dann 2 kürzen.
D=Q\{-1}
e) Ergebnis: 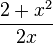
D=Q\{0}
f) Ergebnis: 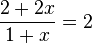
Hier kann man im Ergebnis im Zähler 2 ausklammern und dann beim Bruch 1+x kürzen.
D=Q\{-1}
g) Hauptnenner ist das Produkt der beiden Nenner x - 1 und x. Erweitere die beiden Brüche passend und fasse dann zusammen.
Ergebnis: 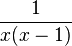
Vor dem Minuend steht ein Minuszeichen, dies bedeutet, wenn man die Zähler zusammenfasst x - (x-1), setze dazu den zweiten Zähler in Klammern! - und vereinfache dann.
D=Q\{0;1}
h) Ergebnis: 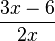
D=Q\{0}
i) Ergebnis: 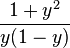
D=Q\{0;1}
j) Hier hast du 3 Brüche gegeben. Hauptnenner ist die höchste gemeinsame x-Potenz hier also x2.
Ergebnis: 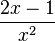
Hauptnenner ist x2,also erweitert man den 1. udn 3. Bruch jeweils mit x und der gemeinsame Zähler ist dann x-x2-(1-x2)+x, Klammern auflösen und zusammenfassen liefert 2x-1
D=Q\{0}
k) Den Zähler des 1. Bruches musst du ausmultiplizieren. Den Minuend 2x kann man als Bruch mit dem Nenner 0,5x schreiben, indem man den Bruch 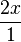 mit 0,5x erweitert, also
mit 0,5x erweitert, also 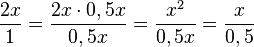 .
.
Ergebnis: 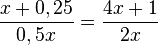 , den letzten Bruch erhältst du in dem du mit 4 erweiterst.
, den letzten Bruch erhältst du in dem du mit 4 erweiterst.
Es ist (x+0,5)2=(x+0,5)(x+0,5), ausmultiplizieren liefert x2+x+0,25
D=Q\{0}
l) Für die Terme im Nenner gilt das Kommutativgesetz.
Ergebnis: 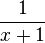
D=Q\{-1}
m) Ergebnis: 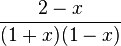
D=Q\{-1;1}
n) Ergebnis: 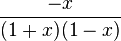
D=Q\{-1;1}
o) Ergebnis: 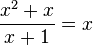
D=Q\{-1}, für den zusammengefassten Term ist D = Q.
p) Ergebnis: 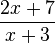 D=Q\{-3}
D=Q\{-3}
2.
Beim Dividieren schreibe zuerst die Mulitplikation mit dem Kehrbruch hin und vereinfache dann.
a) 1
D=Q\{0}, für den zusammengefassten Term ist D = Q.
b) 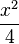
D=Q\{0}, für den zusammengefassten Term ist D = Q.
c) Im Zähler des 2. Bruches kann man 5 ausklammern. Nach der Multiplikation mit dem Kehrbruch hat man in Zähler und Nenner gemeinsame Faktoren 2 und x - 2, die man kürzen kann.
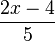
Im Zähler steht der Faktor 4 im Nenner 10, also kann man den Bruch nach Kürzen mit dem Faktor x + 2 noch mit 2 kürzen.
D=Q\{0}, für den vereinfachten Term ist D = Q.
d) Das Minuszeichen vor dem Divisor kann man vor den Gesamtterm schreiben.
-x
D=Q\{0}, für den zusammengefassten Term ist D = Q.
e) Beachte: Hier werden 2 Brüche multipliziert!.
Im Zähler bei 1-x kann man - ausklammern und dann steht im Zähler auch x-1, wie im Nenner des 2. Bruches und das - schreibt man vor den Bruch.
-4x4
Beachte, dass 1-x = -(-1+x) = -(x-1) ist.
D=Q\{0;1}, für den zusammengefassten Term ist D = Q.
f) 1
D=Q.
g) Fasse zuerst die zwei Brüche in der Klammer zusammen. 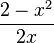 und dann werden zwei Brüche multipliziert.
und dann werden zwei Brüche multipliziert.
2-x2
D=Q\{0}, für den zusammengefassten Term ist D = Q.
h) Fasse auch hier zuerst die zwei Brüche in der Klammer zusammen und dividiere dann.

D=Q\{0}
i) Klammer berechnen 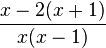 und dann dividieren.
und dann dividieren.
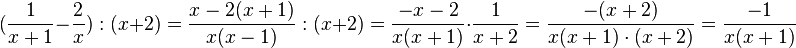
Im Zähler steht -x-2 = -(x+2) und x+2 kann man kürzen! Gut, dass man den Zähler nicht ausmultipliziert hat, da sieht man den Faktor x+2 zum Kürzen.
D=Q\{-2;-1;0}, für den zusammengefassten Term ist D = Q\{-1;0}.
j) Auch hier zuerst die Klammer berechnen und ann multiplizieren.
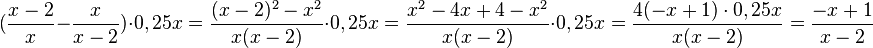
D=Q\{0;2}, für den zusammengefassten Term ist D = Q\{2}.
3.
a). Die Terme von T3 und T4 werden multipliziert, also (Zähler mal Zähler) durch (Nenner mal Nenner)
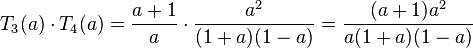
In Zähler und Nenner kommen die Faktoren a und (a+1) vor, also kann man sie kürzen. Es bleibt 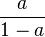 .
.
b) Term T2 wird durch Term T4 geteilt, also mache zuerst den Kehrbruch von T4 und multipliziere dann.
![T_2 (a) : T_4 (a)= \frac{a}{a-1} : \frac{a^2}{(1+a)(1-a)} = \frac{a}{a-1} \cdot \frac{(1+a)(1-a)}{a^2} = \frac{a(1+a)(1-a)}{(a-1)a^2} = \frac{a(1+a)[-(a-1)]}{(a-1)a^2}](/images/math/f/0/a/f0a3ce57a47918c4dbcececc8ada6eb4.png) - Buchstabe E
- Buchstabe E
In Zähler und Nenner hat man a und (a-1) als gemeinsame Faktoren, die man kürzen kann und es bleibt 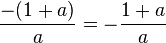 - Buchstabe E
- Buchstabe E
c) Der Term T5 wird vom Term T3 subtrahiert. Man muss also den gemeinsamen Nenner finden. T3 und T5 haben beide den Nenner a, also nehmen wir den gleich. 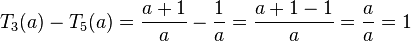 - Buchstabe O
- Buchstabe O
d) Der Term T4 wird zum Term T2 addiert. Man muss also den gemeinsamen Nenner finden. Der Nenner von T2 ist (a-1), der Nenner von T4 ist (1-a)(1+a). Es ist a-1 = -(1-a). Es ist also 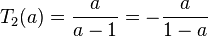 . Also kommt in beiden Nennern der Faktor (1-a) vor. Der Hauptnenner ist also (1+a)(1-a). Nun muss man den T2 mit 1+a erweitern.
. Also kommt in beiden Nennern der Faktor (1-a) vor. Der Hauptnenner ist also (1+a)(1-a). Nun muss man den T2 mit 1+a erweitern.
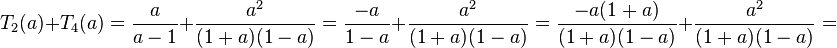
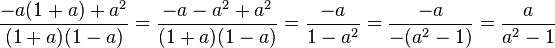 - Buchstabe T
- Buchstabe T
e) Der Term T1 wird durch den Term T3 dividiert. Bilde zuerst den Kehrbruch von T3 und multipliziere dann die zwei Terme.
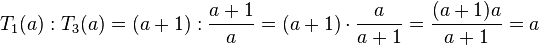 - Buchstabe R
- Buchstabe R
f) Vom Quotienten der Terme T1 und T3 wird a subtrahiert. Den Quotienten T1:T3 hat man gerade ausgerechnet. Das Ergebnis war a. Subtrahiert man a von a, dann ergibt sich 0. - Buchstabe N
g) Der Term T1 wird mit T2 multipliziert und das Produkt durch T3 dividiert.
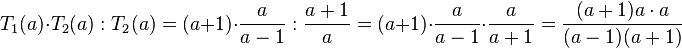
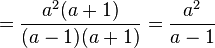 - Buchstabe H
- Buchstabe H
Das waren jetzt Aufgaben nur zum Einüben und Lernen wie man es richtig macht. Nun kommen ein paar Anwendungsaufgaben.
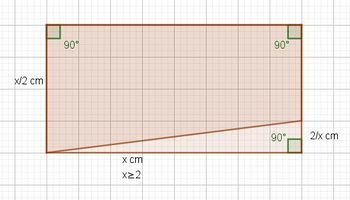
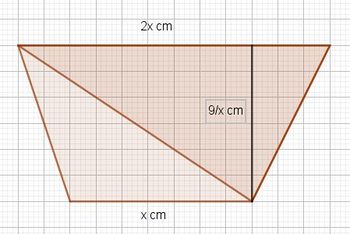
a) Die schraffierte Fläche ist ein Trapezfläche. Die Trapezformel lautet 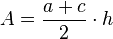 . Mit
. Mit 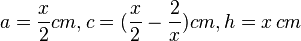 ergibt sich
ergibt sich 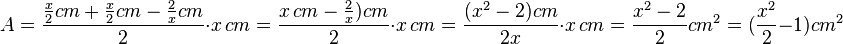
Die Gesamtfläche ist eine Rechtsfläche mit 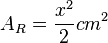 . Der Anteil der schraffierten Fläche an der Rechtecksfläche ist dann
. Der Anteil der schraffierten Fläche an der Rechtecksfläche ist dann 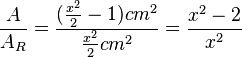 (den Bruch mit 2 erweitern) oder anders geschrieben
(den Bruch mit 2 erweitern) oder anders geschrieben 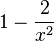
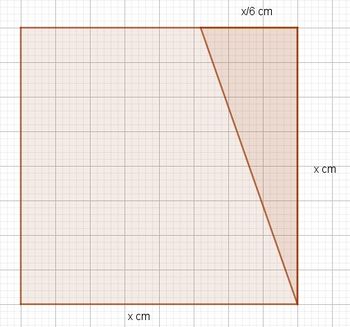
b) Die schraffierte Fläche ist eine Dreiecksfläche. Die Formel für die Dreiecksfläche ist 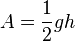 . Mit
. Mit 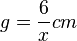 und
und 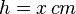 ergibt sich
ergibt sich 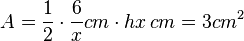
Der Anteil an der Quadratfläche 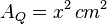 ist dann
ist dann 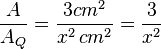 .
.
c) Die schraffierte Fläche ist eine Dreiecksfläche. Es ist 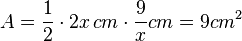
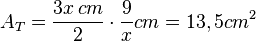 ist
ist 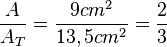
Und nun noch ein paar Aufgaben zum Umformen gebrochen-rationaler Terme:
a) Man kann einen Bruch auch als Divisionsaufgabe schreiben. Es ist 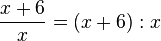 und nach dem Distributivgesetz ist
und nach dem Distributivgesetz ist 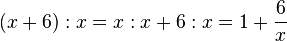 .
.
Bei der Aufgabe (2) addiert man im Zähler mit 3 - 3 eine 0 und zerlegt dann den Bruch auch wieder wie bei (1) indem man mit dem Distrubitivgesetz dividiert. [(x+3) - 3]:(x+3) = (x+3):(x+3) - 3:(x+3). Divisionen kann man auch wieder als Bruch schreiben.
b) 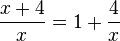
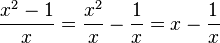
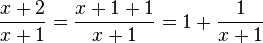
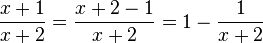
Dies ist nur die Umkehrung der Addition zweier gleichnamiger Brüche. Zwei gleichnamige Brüche addiert man 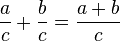 .
.
Liest man die letze Gleichung von rechts nach links, dann steht da 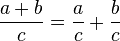 , was man hier angewendet hat.
, was man hier angewendet hat.
c) Folgende Terme sind äquivalent:
(1) und (9),
(2) und (10),
(3), (6) und (11),
(4) und (5),

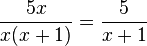
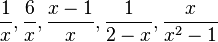 mit
mit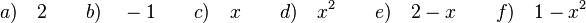
![a) \quad \frac{4}{15} \quad [60xy] \qquad b) \quad \frac{x}{x-y} \quad [2(y-x)] \qquad c) \quad \frac{a}{a-b} \quad [b(a-b)(a+b)] \qquad d) \quad -1 \quad [a+b] \qquad e) \quad ab \quad [ab^3] \qquad](/images/math/3/8/8/3885dd4b649aa70591ddaf2fbcc94022.png)
![f) \quad -\frac{2}{3} \quad [-6b] \qquad g) \quad \frac{4y}{y+x} \quad [-x(x+y)] \qquad h)\quad x \quad [x(1-x)] \qquad i) \quad 2 \quad [x+3] \qquad j) \quad xy \quad [x^2y^5] \qquad](/images/math/8/7/9/8794650e42a7c04481875b6e92dc6226.png)
![k) \quad \frac{1}{a-b} \quad [b-a]](/images/math/e/f/2/ef2c458cac76722814478a39fcfa7059.png)
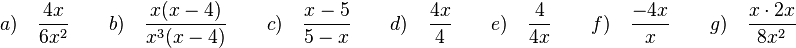
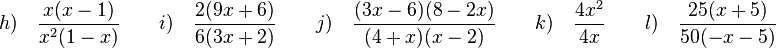
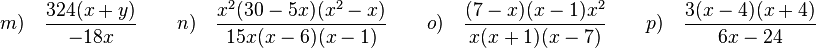
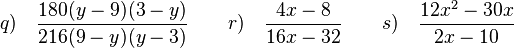
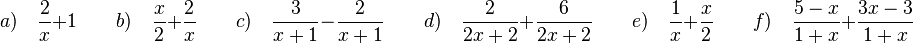
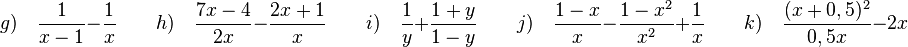
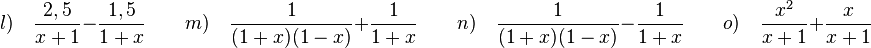
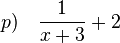
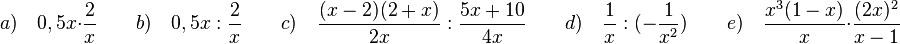
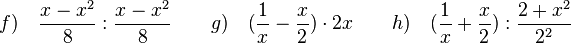
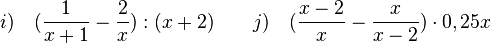
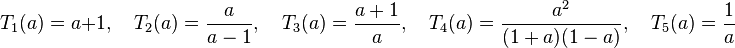

![e) \quad T_1(a) : T_3(a) \qquad f) \quad T_1(a) : T_3(a) - a \qquad g)\quad [T_1(a) \cdot T_2(a)] :T_3(a)](/images/math/d/5/a/d5a4bae747d1b6fb9dee2a7add718eeb.png)
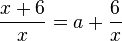 und (2)
und (2) 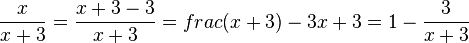 .
.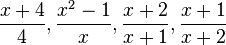 als Summe bzw. Differenz.
als Summe bzw. Differenz.