M8 Rechnen mit Doppelbrüchen
Doppelbrüche hast du in der 6. Klasse kennengelernt. In diesen Videos
kannst du es nochmals wiederholen.
Bearbeite die Aufgaben auf dieser Seite
In diesem Video
wird erkärt, wie man Doppelbrüchen aus Buchstaben auflöst.
Auf dieser Seite ist auch nochmals schriftlich erklärt wie man Doppelbrüche auflöst.
30px Merke
Ein Doppelbruch ist einfach aufzulösen, wenn man berücksichtigt, dass ein Bruch nur eine andere Schreibweise einer Division ist. Und man dividiert durch einen Bruch, indem man mit seinem Kehrwert multipliziert. 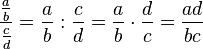 Beachte: Kürzen geht nur, wenn in Zähler und Nenner Produkte stehen! |
Das geht mit allen Brüchen! Auch wenn sie "wild" aussehen.
1. Beispiel: Der Doppelbruch 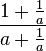 wird zuerst in einen "echten Doppelbruch" verwandelt, d.h. Zähler und Nenner als Bruch schreiben.
wird zuerst in einen "echten Doppelbruch" verwandelt, d.h. Zähler und Nenner als Bruch schreiben. 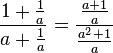 Diesen Doppelbruch löst man nun auf:
Diesen Doppelbruch löst man nun auf: 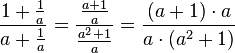 . Nun kann man a kürzen.
. Nun kann man a kürzen. 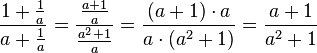 - Hier geht nichts mehr zu kürzen, also ist man fertig!
- Hier geht nichts mehr zu kürzen, also ist man fertig!
2. Beispiel:
Auch diesen Doppelbruch 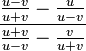 schreibt man zuerst als "echten Doppelbruch":
schreibt man zuerst als "echten Doppelbruch": 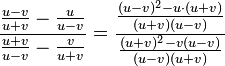
Die beiden Nenner lässt man als Produkte stehen!
Nun löst man den Doppelbruch auf: (u+v)}{[(u+v)^2-v(u-v)](u+v)(u-v)}](/images/math/6/5/6/65695d26baa5e74d217348106c85847e.png)
Nun kann man in Zähler und Nenner 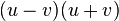 kürzen.
kürzen.
(u+v)}{[(u+v)^2-v(u-v)](u+v)(u-v)}=\frac{(u-v)^2-u \cdot (u+v)}{(u+v)^2-v(u-v)}](/images/math/4/7/a/47a564132d89b7f0abb1434a06faed69.png)
In Zähler und Nenner stehen Summen bzw. Differenzen. Man kann auch nichts mehr ausklammern. Dann löst man in Zähler und Nenner noch die Klammern auf und fasst zusammen.