M8 Term und Graph bei gebrochen-rationalen Funktionen
Auf dieser Seite soll der Zusammenhang zwischen dem Graphen und dem Funktionsterm einer gebrochen-rationalen Funktion näher untersucht werden. Dabei geht es um zwei Fragestellungen:
1. Wie finde ich aus einem gegebenen Graphen den passenden Funktionsterm.
2. Wie kann man "leicht" aus einem gegebenen Funktionsterm den Graphen angeben.
Zur Beantwortung sind die folgenden Eigenschaften gebrochen-rationaler Funktionen hilfreich.
Ausgangspunkt unserer Betrachtungen ist die indirekte Proportionalität 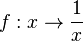 . Die Funktion ist für
. Die Funktion ist für 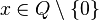 definiert. Die Funktionsgleichung ist
definiert. Die Funktionsgleichung ist 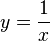 und der Funktionsgraph
und der Funktionsgraph
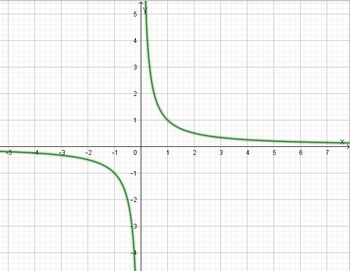
In allen Applets sind die Funktionsterme mit angegeben. Beachte wie sich die Funktionsterme bei Änderung der Parameter ändern.
Stelle den Wert am Schieberegler ein und schaue wo dieser Wert im Funktionsterm auftaucht.
Inhaltsverzeichnis |
Definitionslücke - senkrechte Asymptote
Die Funktion 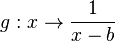 ist für
ist für 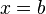 nicht definiert, da wenn man b für x einsetzt im Nenner Null steht. Das ist nicht zulässig! Also ist
nicht definiert, da wenn man b für x einsetzt im Nenner Null steht. Das ist nicht zulässig! Also ist 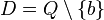 . An der Stelle
. An der Stelle 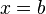 hat die Funktion
hat die Funktion  eine Definitionslücke. Der Graph eine senkrechte Asymptote.
eine Definitionslücke. Der Graph eine senkrechte Asymptote. 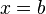 ist eine Polstelle des Graphen.
ist eine Polstelle des Graphen.
1. Die Funktionsgleichung ist 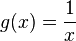 und die Gleichung der Asymptote
und die Gleichung der Asymptote 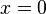 .
.
2. Der Graph von f der indirekten Proportionalität wird um 1 in positive x-Richtung verschoben.
Ebenso wird die Asymptote um 1 in positive x-Richtung verschoben.
Die Funktionsgleichung ist 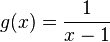 und die Gleichung der Asymptote
und die Gleichung der Asymptote 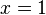 .
.
3. Der Graph von f der indirekten Proportionalität wird um 2 in negative x-Richtung verschoben.
Ebenso wird die Asymptote um 2 in negative x-Richtung verschoben.
Die Funktionsgleichung ist 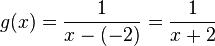 und die Gleichung der Asymptote
und die Gleichung der Asymptote 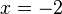 .
.
4. Der Graph von f wird um b in x-Richtung verschoben.
Ist b > 0, dann erfolgt die Verschiebung von f um b in positive x-Richtung,
ist b < 0, erfolgt die Verschiebung um den Betrag von b, in negative x-Richtung.
|
Merke:
Den Graphen der Funktion
|
Zusammenfassung:
Für die anfangs gestellten zwei Fragen hast du nun folgende Antworten:
1. Hat der Graph für 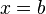 eine Definitionslücke und senkrechte Asymptote, dann steht im Nenner der
eine Definitionslücke und senkrechte Asymptote, dann steht im Nenner der
gebrochen-rationalen Funktion der Term 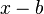 oder eine Potenz
oder eine Potenz 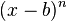 .
.
2. Ist 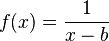 , dann erhältst du den Graphen durch Verschiebung des Graphen von
, dann erhältst du den Graphen durch Verschiebung des Graphen von 
um b in Richtung der x-Achse. Die Asymptote ist 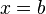
3. Beachte dabei, dass im Nenner 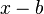 steht. D.h. wenn du für
steht. D.h. wenn du für 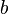 eine negative Zahl z.B. b = -3 einsetzt, dann steht im Nenner
eine negative Zahl z.B. b = -3 einsetzt, dann steht im Nenner 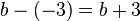 , also die Zahl mit anderem Vorzeichen!
, also die Zahl mit anderem Vorzeichen!
Spiegelung an der x-Achse
Im folgenden Applet ist der Graph der indirekten Proportionalität f mit 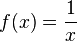 ( grün) und der Graph der Funktion g mit
( grün) und der Graph der Funktion g mit 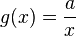 ( rot) eingezeichnet. Mit dem Schieberegler kannst du den Wert von a zwischen den Werten a = -1 und a = 1 ändern.
( rot) eingezeichnet. Mit dem Schieberegler kannst du den Wert von a zwischen den Werten a = -1 und a = 1 ändern.
|
Merke:
Den (roten) Graphen der Funktion |
Anmerkung:
Du könntest natürlich auch sagen, dass du den grünen Graph an der y-Achse spiegelst. Das Ergebnis ist das gleiche!
Aber wenn du die Funktionsterme anschaust dann hat die Funktion  den Funktionswert
den Funktionswert 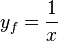 . Und die Funktion
. Und die Funktion  hat den Funktionswert
hat den Funktionswert 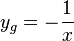 , also ist
, also ist 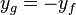 , der y-Wert ändert also sein Vorzeichen. Das entspricht der Spiegelung an der x-Achse.
, der y-Wert ändert also sein Vorzeichen. Das entspricht der Spiegelung an der x-Achse.
Streckung und Stauchung
Im folgenden Applet ist der Graph der indirekten Proportionalität f mit 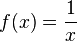 ( grün) und der Graph der Funktion g mit
( grün) und der Graph der Funktion g mit 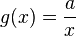 ( rot) eingezeichnet. Mit dem Schieberegler kannst du den Wert von a zwischen den Werten a = 1 und a = 2 ändern. Desweiteren sind für x = -2 und x = 1 die y-Strecken von der x-Achse zum Graphen eingezeichnet.
( rot) eingezeichnet. Mit dem Schieberegler kannst du den Wert von a zwischen den Werten a = 1 und a = 2 ändern. Desweiteren sind für x = -2 und x = 1 die y-Strecken von der x-Achse zum Graphen eingezeichnet.
Stellt man den Schieberegler auf a = 2, dann werden die Abstände der Punkte auf den Graphen
von der x-Achse größer. Bei x = -2 ist zuerst der Abstand des Punktes (-2;-0,5) von der x-Achse 0,5. Nach Bestätigung
des Reglers ist der Abstand des Punktes (-2;-1) auf dem roten Graphen von der x-Achse 1.
Aus dem y-Wert -0,5 wird also der y-Wert -1.
Ebenso ist es bei x = 1. Aus dem y-Wert 1 wird der y-Wert 2.
Alle y-Werte  der Funktion f werden mit a multipliziert und man erhält den
der Funktion f werden mit a multipliziert und man erhält den 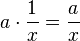 .
.
Wenn a > 1 ist, dann wird der grüne Graph (Graph von  ) um den Faktor a in y-Richtung gestreckt und man erhält den roten Graph (Graph von
) um den Faktor a in y-Richtung gestreckt und man erhält den roten Graph (Graph von  ) .
) .
 ) um den Faktor a in y-Richtung gestaucht und man erhält den roten Graph (Graph von
) um den Faktor a in y-Richtung gestaucht und man erhält den roten Graph (Graph von  ) .
) .
Und was ist, wenn a nun auch noch negativ ist?
|
Merke:
Bei der Funktion Wenn a > 1 ist, dann wird der grüne Graph (Graph von Wenn 0 < a < 1 ist, dann wird der grüne Graph (Graph von Ist a negativ, dann spiegelt man den Graph von |
Verschiebung in y-Richtung
Die blauen Pfeile verbinden für gleiches x die entsprechenden y-Werte auf den Graphen von f und g.
Die Pfeile sind alle gleich lang und parallel. Ihre Länge ist der Betrag von c.
|
Merke:
Zu jedem Funktionswert Man erhält den Graph der Funtkion Ist c positiv (c > 0)erfolgt die Verschiebung in positive y-Richtung, |
Nullstellen
Du kennst die Aussage:
Ein Bruch hat den Wert Null, wenn sein Zähler den Wert Null hat.
Dies wollen wir nun verwenden und gebrochen-rationale Funktionen vom Typ  mit
mit 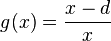 betrachten. Im Zähler steht nun ein linearer Term
betrachten. Im Zähler steht nun ein linearer Term 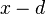 bei dem der Parameter d für eine rationale Zahl steht.
bei dem der Parameter d für eine rationale Zahl steht.
Da nun im Zähler ein linearer Term steht, kann dieser den Wert Null annehmen. Dies passiert, wenn 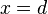 ist. Also ist
ist. Also ist 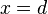 eine Nullstelle der Funktion
eine Nullstelle der Funktion  .
.
Betätigt man den Schieberegler dann ändert die Nullstelle ihre Lage.
Die Definitionslücke bzw. Polstelle und die senkrecht Asymptote x = 0 bleiben unverändert.
waagrechte Asymptote
Bei den Beispielen zu "Nullstelle" ist eine waagrechte Asymptote für  eingezeichnet. Diese Gerade ist für alle Beispiele von Aufgabe 7 waagrechte Asymptote. Für andere gebrochen-rationale Funktionen kann die waagrechte Asymptote auch anders liegen. Dies wird in den nächsten Aufgaben veranschaulicht.
eingezeichnet. Diese Gerade ist für alle Beispiele von Aufgabe 7 waagrechte Asymptote. Für andere gebrochen-rationale Funktionen kann die waagrechte Asymptote auch anders liegen. Dies wird in den nächsten Aufgaben veranschaulicht.
Für 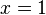 ist der Funktionsterm nicht definiert. Die Definitionsmenge ist D = Q\{0}.
ist der Funktionsterm nicht definiert. Die Definitionsmenge ist D = Q\{0}.
Für a = 0 ist g(x) = 0, also die konstante Funktion 0, die allen x-Werten den y-Wert y = 0 zuordnet.
Graphisch hast du in der Aufgabe 8 gesehen, dass die Funktionswerte für  sich der waagrechten Asymptote
sich der waagrechten Asymptote 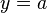 beliebig nahe annähern. Dies kann man auch am Funktionsterm sehen. Man betrachtet den Funktionsterm
beliebig nahe annähern. Dies kann man auch am Funktionsterm sehen. Man betrachtet den Funktionsterm 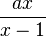 für
für  . Setzt man für x sehr sehr große Zahlen ein, dann steht dort sowas wie "
. Setzt man für x sehr sehr große Zahlen ein, dann steht dort sowas wie "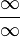 ". Was soll das sein?????
". Was soll das sein?????  ist kein Element der rationalen Zahlen, also können wir auch nicht mit
ist kein Element der rationalen Zahlen, also können wir auch nicht mit  rechnen!
rechnen!
Am Graphen sehen wir ja das Ergebnis, dass für  die Gerade
die Gerade 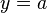 waagrechte Asymptote ist.
waagrechte Asymptote ist.
Mit einem Trick kann man es aber auch am Funktionsterm sehen. Dazu klammert man in Zähler und Nenner x aus und kürzt x.
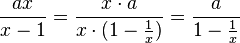
Im Nenner steht nun der Term 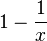 . Wenn nun
. Wenn nun 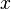 gegen
gegen  geht, dann wird
geht, dann wird  sehr sehr kleiner,
sehr sehr kleiner,  geht gegen 0 (das sieht du auch oben am Anfang der Seite beim Graphen der indirekten Proportionalitität). Wenn
geht gegen 0 (das sieht du auch oben am Anfang der Seite beim Graphen der indirekten Proportionalitität). Wenn  gegen 0 geht für x gegen
gegen 0 geht für x gegen  , dann wir geht der Nenner
, dann wir geht der Nenner 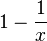 gegen den Wert 1. Und das ist eine Eigenschaft der Asymptote, dass sich die Funktionswerte ihr beliebig nahe annähern.
gegen den Wert 1. Und das ist eine Eigenschaft der Asymptote, dass sich die Funktionswerte ihr beliebig nahe annähern.
Für den Fall  darf man im Funktionsterm dann auch
darf man im Funktionsterm dann auch 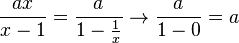 schreiben.
schreiben.
Dies soll nun am Beispiel in Aufgabe 9 nochmals gemacht werden. Hier steht nun im Nenner der Term 2x-1.
Der Term im Nenner der Funktion g ist nicht mehr x - 1, sondern 2x - 1. Außerdem hat die waagrechte Asymptote nicht mehr die Gleichung y = 1, sondern 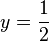 .
.
Betätigt man den Schieberegler "verschiebt" sich der Funktionsgraph und die waagrechte Asymptote. Tatsächlich wird der Graph von g auch gestreckt (,wenn a < -1 oder a > 1 ist) oder gestaucht (,wenn -1 < a < 1 ist).
Der Trick war:
1. In Zähler und Nenner x ausklammern.
2. x kürzen.
2. x gegen  gehen lassen und schauen was der Nenner macht.
gehen lassen und schauen was der Nenner macht.
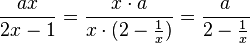
Für  geht
geht  wieder gegen 0, der Nennerterm
wieder gegen 0, der Nennerterm 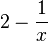 dann gegen 2 und der Funktionsterm
dann gegen 2 und der Funktionsterm 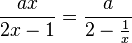 also gegen
also gegen 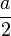 . Die Gleichung der waagrechten Asymptote ist also
. Die Gleichung der waagrechten Asymptote ist also 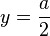 .
.
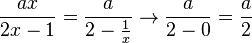 schreiben.
schreiben.Vorzeichenwechsel
Beim Graphen der Funktion 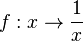 sieht man, dass bei Annäherung von x an 0 die y-Werte unterschiedliches Verhalten zeigen.
sieht man, dass bei Annäherung von x an 0 die y-Werte unterschiedliches Verhalten zeigen.
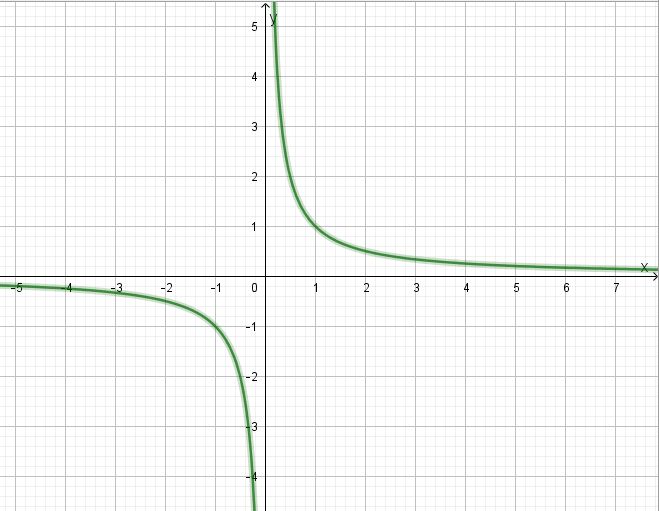
Nähert man sich von links (also von negativen Zahlen) der 0, so werden die y-Werte immer kleiner (d.h. sie werden vom Betrag her immer größer, aber da sie negativ sind, gibt das ganz große negative Zahlen), sie gehen also gegen 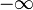 .
.
Nähert man sich von rechts (also von positiven Zahlen) der 0, so werden die y-Werte immer größer (d.h. da sie positiv sind wird ihr Betrag immer größer) und sie gehen gegen  .
.
Je nach Annäherung an 0 gehen die y-Werte einmal nach 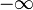 und von der anderen Seite nach
und von der anderen Seite nach  . Man spricht hier von einem Vorzeichenwechsel -/+ (man geht den üblichen Weg für x von links nach rechts).
. Man spricht hier von einem Vorzeichenwechsel -/+ (man geht den üblichen Weg für x von links nach rechts).
Anders verhält es sich beim Graphen der Funktion 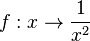 .
.
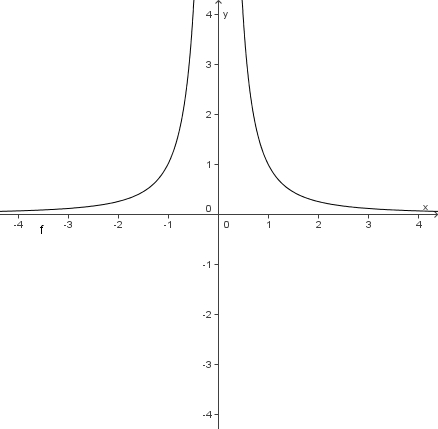
Da im Nenner 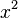 steht, spielt das Vorzeichen von x keine Rolle. Egal ob x negativ oder positiv ist
steht, spielt das Vorzeichen von x keine Rolle. Egal ob x negativ oder positiv ist 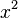 ist stets positiv. Wenn x nun gegen 0 geht (egal von welcher Seite, ob vom negativen oder vom positiven), dann wird der y-Wert
ist stets positiv. Wenn x nun gegen 0 geht (egal von welcher Seite, ob vom negativen oder vom positiven), dann wird der y-Wert 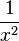 immer größer und geht in beiden Fällen gegen
immer größer und geht in beiden Fällen gegen  . Hier tritt kein Vorzeichenwechsel auf, da hier die y-Werte stets positiv sind.
. Hier tritt kein Vorzeichenwechsel auf, da hier die y-Werte stets positiv sind.
Bei ungeraden n (, also n = 1, 3, 5, ....) tritt ein Vorzeichenwechsel auf.
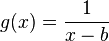 (
(
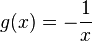 erhältst du aus dem (grünen) Graphen der Funktion
erhältst du aus dem (grünen) Graphen der Funktion 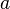 multipliziert.
multipliziert.
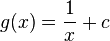 (
( addiert und man erhält
addiert und man erhält 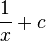 .
.
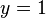 für
für 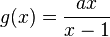 (
(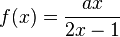 (
(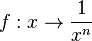 variieren.
variieren.

