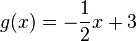Bruchgleichungen
Bei den Bruchgleichungen der 8. Klasse hast du schon Gleichungen wie 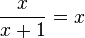 gelöst. Als Lösung hast du x=0 erhalten. Das konntest du lösen. Aber bei einer Gleichung wie
gelöst. Als Lösung hast du x=0 erhalten. Das konntest du lösen. Aber bei einer Gleichung wie 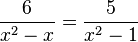 mit der Definitionsmenge D = R\{-1;0;1} gab es schon Probleme. Wie löse ich dies?
mit der Definitionsmenge D = R\{-1;0;1} gab es schon Probleme. Wie löse ich dies?
Wenn du die Bruchgleilchung 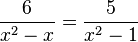 mit dem Produkt der Nenner (x2-x)(x2-1) multiplizierst, dann erhältst du:
mit dem Produkt der Nenner (x2-x)(x2-1) multiplizierst, dann erhältst du:
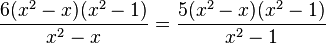 und gekürzt ("über Kreuz multiplizieren"):
und gekürzt ("über Kreuz multiplizieren"):
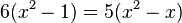
Man kann nun zusammenfassen und vereinfachen: 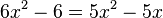 -->
--> 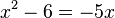 -->
--> 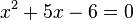 das ist eine quadratische Gleichung, die du lösen kannst.
das ist eine quadratische Gleichung, die du lösen kannst.

Aufgabe 1
Bestimme für die Bruchgleichung 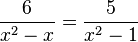 die Definitionsmenge und ermittle dann die Lösungsmenge L.
die Definitionsmenge und ermittle dann die Lösungsmenge L.
[Lösung anzeigen][Lösung ausblenden]
Da unsere Grundmenge R ist, ist D=R\{-1,0,1}; die quadratische Gleichung
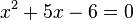
hat die Lösungen
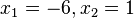
. Allerdings ist
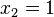
nicht in der Definitionsmenge, also ist L={-6}.

Aufgabe 2
Bestimme für die Bruchgleichungen jeweils die maximale Definitionsmenge und den Hauptnenner. Löse dann die Gleichungen.
a) 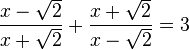
b) 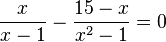
[Lösung anzeigen][Lösung ausblenden]
a) 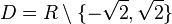 ,
,
Man bestimmt zuerst den Hauptnenner (HN) und multipliziert die Gleichung dann mit dem Hauptnenner.
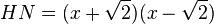
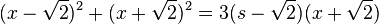
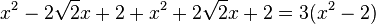
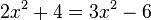
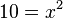 , also
, also 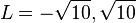 }
}
b) D=R\{-1;1} (3. binomische Formel x2-1=(x-1)(x+1)!) ,
Die zwei Brüche auf der linken Seite haben die Nenner x-1 und x²-1. Mit der dritten binomischen Formel kommt in beiden Nenner x-1 vor, also muss man den ersten Bruch mit x+1 erweitern. Dann haben beiden Brüche den gleichen Nenner (x+1)(x-1). Multipliziert man nun die Gleichung mit (x+1)(x-1) durch, dann fallen die Nenner weg und links bleibt stehen x(x+1)-(15-x). Bitte macht eine Klammer um den Zähler des zweiten Bruchs, weil vor dem Bruch ein - steht! Damit muss man die Gleichung x
2+x-15+x=0 zu lösen, dies ist eine quadratische Gleichung x
2+2x-15=0 mit den zwei Lösungen x
1=-5; x
2=3
Anwendungsaufgaben

Aufgabe 3
1. a) Finde eine positive reelle Zahl, die um 1 kleiner als ihr Quadrat ist.
b) Finde eine reelle Zahl, die um 1 größer als ihr Kehrwert ist.
2. In einem rechtwinkligen Dreieck ist die längere Kathete um 1 cm kürzer als die Hypotenuse, aber um 7cm länger als die kürzere Kathete. Berechne die Längen der drei Dreiecksseiten.
Konstruiere das Dreieck und seinen Umkreis.
Ermittle die Umfangslänge und den Flächeninhalt dieses Dreiecks. wie viel lProzent der Umrkeisfläche nimmt die Dreiecksfläche ein?
3. Ein Volleyballverein bietet seinen Fans eine Busfahrt zum Auswärtsspiel an. Es wird mit einem vollen Bus gerechnet, der insgesamt 450 € kostet. Bei der Abfahrt erscheinen aber fünf der angemeldeten Personen nicht, so dass sich der Fahrpreis für jeden der übrigen Fans um 1 € verteuert. Finde heraus, um wie viel Proeznt sich durch das Fernbleiben der fünf Fans die Fahrt für jeden der übrigen verteuert.
[Lösung anzeigen][Lösung ausblenden]
1a) Die zugehörige Gleichung ist 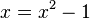 mit der positven Lösung
mit der positven Lösung 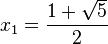 .
.
b) Die zugehörige Gleichung ist 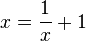 mit den Lösungen
mit den Lösungen 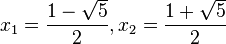
2. Mache dir zuerst eine Skizze eines rechtwinkligen Dreiecks (Hypotenuse c unten, Katheten rechts und links, z.b. die rechte Kathete länger, dann ist die längere Kathete b, die kürzere a) Es ist dann a = b-7, c = b+1 und mit dem Satz von Pythagoras erhält man 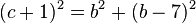 . Nun löst man die Klammern auf und fasst zusammen. Es ergibt sich die quadratische Gleichung
. Nun löst man die Klammern auf und fasst zusammen. Es ergibt sich die quadratische Gleichung 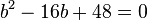 , welche die Lösungen
, welche die Lösungen 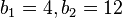 . Wegen a = b-7 ist b1=4 keine Lösung, also hat das Dreieck die Seitenlängen a = 5, b = 12, c = 13.
. Wegen a = b-7 ist b1=4 keine Lösung, also hat das Dreieck die Seitenlängen a = 5, b = 12, c = 13.
(Übrigens ist (5;12;13) ein pythagroräisches Zahlentripfel!)
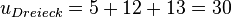 ,
, 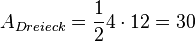
Der Umkreis hat den Radius 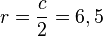 (Thaleskreis!), also ist
(Thaleskreis!), also ist 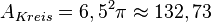
Es ist 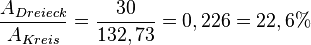
3. Für den vollen Bus sind n Mitfahrer eingeplant. Jeder Mitfahrer zahlt dann für die Busfahrt 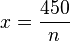 .
.
Da nun 5 Personen weniger mitfahren, es ist also die Anzahl der Mitfahrer n - 5. Und jeder Mitfahrer zahlt nun x + 1.
Man hat nun die Gleichung 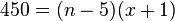 . Diese Gleichung hat nun zwei Unbekannte n und x. Wir kennen aber einen Zusammenhang zwischen n und x, nämlich
. Diese Gleichung hat nun zwei Unbekannte n und x. Wir kennen aber einen Zusammenhang zwischen n und x, nämlich 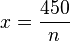 oder
oder 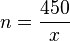 . Setzt man die letzte Gleichung für n in die Gleichung
. Setzt man die letzte Gleichung für n in die Gleichung 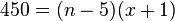 ein, so erhält man
ein, so erhält man 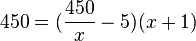 .
Die Gleichung
.
Die Gleichung 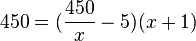 kann man in eine quadratische Gleichung umwandeln, indem man sie mit
kann man in eine quadratische Gleichung umwandeln, indem man sie mit 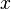 multipliziert (und dabei auf der rechten Seite die erste Klammer als
multipliziert (und dabei auf der rechten Seite die erste Klammer als 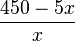 schreibt, dann fällt nämlich beim Multiplizieren mit x der Nenner weg.)
schreibt, dann fällt nämlich beim Multiplizieren mit x der Nenner weg.)
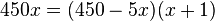
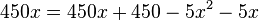
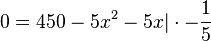
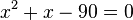 mit den zwei Lösungen
mit den zwei Lösungen 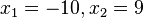 .
.
Also war ursprünglich geplant, dass 50 Mitfahrer jeweils 9€ zahlen. Nun sind es 45 Mitfahrer und jeder zahlt 10€.
Und zum Anschauen (du kannst natürlich auch immer anhalten und selbst mitrechnen und lösen!):

Aufgabe 4
Schwimmbadaufgabe: Adele springt im Schwimmbad mit Anlauf waagrecht vom 10m-Turm. Nach dem Absprung beschreibt sie eine Parabelbahn. Eine Videoaufzeichnung zeigt, dass sie die 5m-Plattform in einem Abstand von 5,0 m passiert.
a) Wähle ein passendes Koordinatensystem und beschreibe Adeles Bahn durch einen Funktionsterm.
b) Wie weit ist Adele in waagrechter Richtung gesprungen?
[Lösung anzeigen][Lösung ausblenden]
a) Koordinatensystem mit Ursprung im Fußpunkt des Sprungturms, Scheitel bei (0;10), weiterer Parabelpunkt (5;5)
Mit der Scheitelform 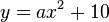 und
und 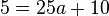 ergibt sich
ergibt sich 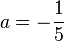 , also
, also 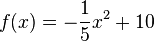
b) Sie kommt bei x unten auf und x erhält man aus
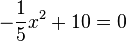
, also
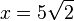
.
Schnittprobleme
1. Man hat zwei Funktionen, eine quadratische Funktion 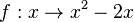 und eine lineare Funktion
und eine lineare Funktion 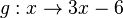 . Für diese zwei Funktionen stellt sich die Frage, haben sie gemeinsame Punkte oder nicht.
. Für diese zwei Funktionen stellt sich die Frage, haben sie gemeinsame Punkte oder nicht.
Für die Graphen der Funktionen bedeutet das, schneiden sie sich, berühren sie sich oder haben sie keine gemeinsamen Punkte.
Dies kann man versuchen graphisch zu lösen:
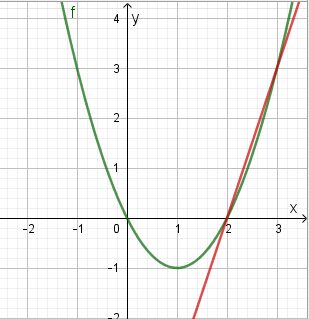
Aus der Grafik liest man ab, dass die beiden Graphen sich in den Punkten (2;0) und (3;3) schneiden.
Rechnerisch geht es darum die Gleichung 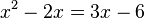 zu lösen. Dazu formt man sie um in die für quadratische Gleichungen übliche Form, alles auf die linke Seite und 0 auf der rechten Seite,
zu lösen. Dazu formt man sie um in die für quadratische Gleichungen übliche Form, alles auf die linke Seite und 0 auf der rechten Seite, 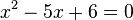 und versucht diese Gleichung zu lösen.
und versucht diese Gleichung zu lösen.
Mit der Diskriminante D =25-24=1 weiß man, dass es zwei Lösungen gibt und mit der Lösungsformel erhält man x1 = 2 und x3 = 3.
2. Die Graphen der Funktionen 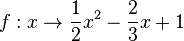 und
und 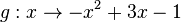 schneiden sich.
schneiden sich.

Aufgabe 5
3. Ermittle die gemeinsamen Punkte der Graphen von 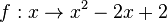 und
und 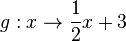 . Zeichnet man die Graphen in ein Koordinatensystem so hat man dieses Bild:
. Zeichnet man die Graphen in ein Koordinatensystem so hat man dieses Bild:
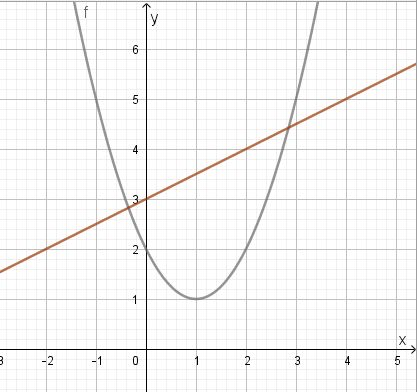
Aus der Graphik kann man die Schnittpunkte schlecht ablesen. Also muss man sie berechnen. Es ist dabei die Gleichung 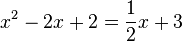 zu lösen. Dies führt zu der quadratischen Gleichung
zu lösen. Dies führt zu der quadratischen Gleichung 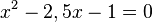 , die man löst und die Lösungen
, die man löst und die Lösungen 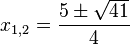 hat, also
hat, also 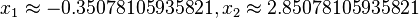
4. Wo schneiden sich die beiden Graphen?
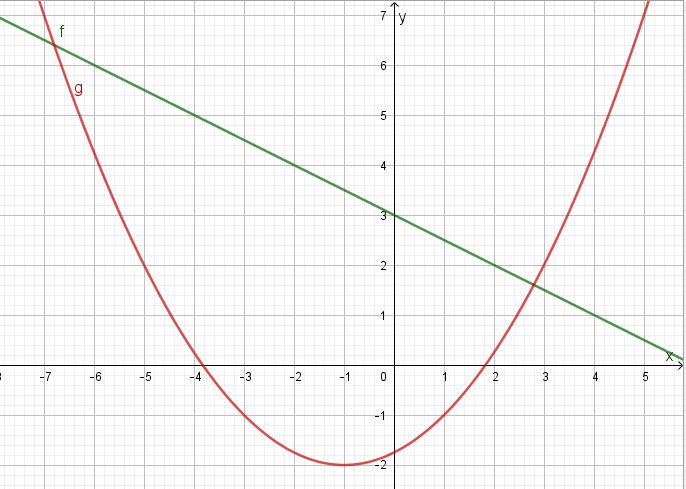
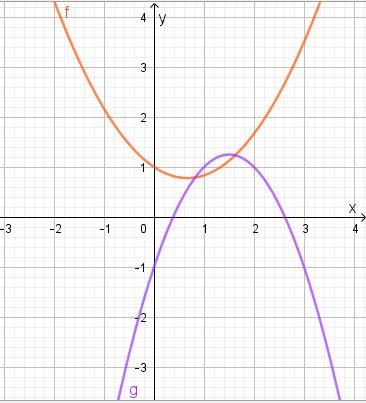
Man kann es aus der Graphik nur ungenau ablesen. Also muss man rechnen. Aber man hat ja nur die zwei Graphen.
Aus den Graphen kann man die Funktonsterme bestimmen. Bestimme die Funktionsgleichungen für f und g.
[Lösung anzeigen][Lösung ausblenden]
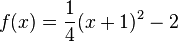
und
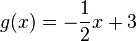
Um die Schnittpunkte zu bestimmen muss man die Gleichung 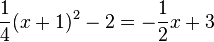 lösen. Dazu formt man die linke Seite zuerst um in
lösen. Dazu formt man die linke Seite zuerst um in 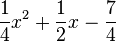 und hat dann die Gleichung
und hat dann die Gleichung 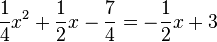 . Diese Gleichung bringt man in die übliche Form einer quadratischen Gleichung
. Diese Gleichung bringt man in die übliche Form einer quadratischen Gleichung 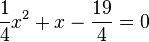 . Mit der Lösungsformel erhält man
. Mit der Lösungsformel erhält man 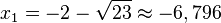 und
und 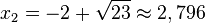
Die Schnittpunkte der beiden Graphen sind dann S1(-6,796;6,398) und S2(2,796;1,602)
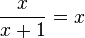 gelöst. Als Lösung hast du x=0 erhalten. Das konntest du lösen. Aber bei einer Gleichung wie
gelöst. Als Lösung hast du x=0 erhalten. Das konntest du lösen. Aber bei einer Gleichung wie 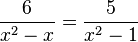 mit der Definitionsmenge D = R\{-1;0;1} gab es schon Probleme. Wie löse ich dies?
mit der Definitionsmenge D = R\{-1;0;1} gab es schon Probleme. Wie löse ich dies? 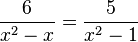 mit dem Produkt der Nenner (x2-x)(x2-1) multiplizierst, dann erhältst du:
mit dem Produkt der Nenner (x2-x)(x2-1) multiplizierst, dann erhältst du: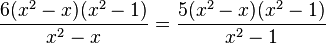 und gekürzt ("über Kreuz multiplizieren"):
und gekürzt ("über Kreuz multiplizieren"):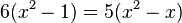
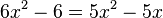 -->
--> 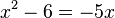 -->
--> 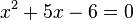 das ist eine quadratische Gleichung, die du lösen kannst.
das ist eine quadratische Gleichung, die du lösen kannst.
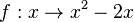 und eine lineare Funktion
und eine lineare Funktion 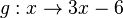 . Für diese zwei Funktionen stellt sich die Frage, haben sie gemeinsame Punkte oder nicht.
. Für diese zwei Funktionen stellt sich die Frage, haben sie gemeinsame Punkte oder nicht. 
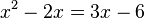 zu lösen. Dazu formt man sie um in die für quadratische Gleichungen übliche Form, alles auf die linke Seite und 0 auf der rechten Seite,
zu lösen. Dazu formt man sie um in die für quadratische Gleichungen übliche Form, alles auf die linke Seite und 0 auf der rechten Seite, 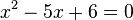 und versucht diese Gleichung zu lösen.
und versucht diese Gleichung zu lösen.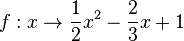 und
und 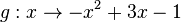 schneiden sich.
schneiden sich. 
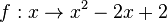 und
und 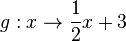 . Zeichnet man die Graphen in ein Koordinatensystem so hat man dieses Bild:
. Zeichnet man die Graphen in ein Koordinatensystem so hat man dieses Bild:
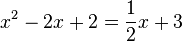 zu lösen. Dies führt zu der quadratischen Gleichung
zu lösen. Dies führt zu der quadratischen Gleichung 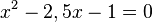 , die man löst und die Lösungen
, die man löst und die Lösungen 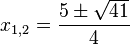 hat, also
hat, also 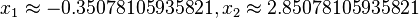

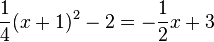 lösen. Dazu formt man die linke Seite zuerst um in
lösen. Dazu formt man die linke Seite zuerst um in 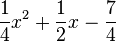 und hat dann die Gleichung
und hat dann die Gleichung 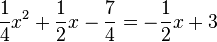 . Diese Gleichung bringt man in die übliche Form einer quadratischen Gleichung
. Diese Gleichung bringt man in die übliche Form einer quadratischen Gleichung 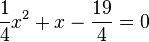 . Mit der Lösungsformel erhält man
. Mit der Lösungsformel erhält man 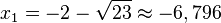 und
und 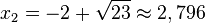
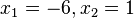 . Allerdings ist
. Allerdings ist 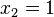 nicht in der Definitionsmenge, also ist L={-6}.
nicht in der Definitionsmenge, also ist L={-6}.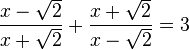
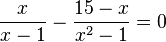
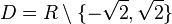 ,
, 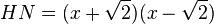
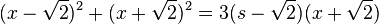
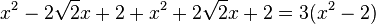
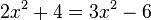
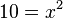 , also
, also 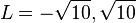 }
}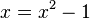 mit der positven Lösung
mit der positven Lösung 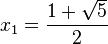 .
.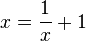 mit den Lösungen
mit den Lösungen 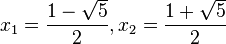
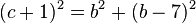 . Nun löst man die Klammern auf und fasst zusammen. Es ergibt sich die quadratische Gleichung
. Nun löst man die Klammern auf und fasst zusammen. Es ergibt sich die quadratische Gleichung 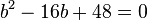 , welche die Lösungen
, welche die Lösungen 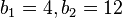 . Wegen a = b-7 ist b1=4 keine Lösung, also hat das Dreieck die Seitenlängen a = 5, b = 12, c = 13.
. Wegen a = b-7 ist b1=4 keine Lösung, also hat das Dreieck die Seitenlängen a = 5, b = 12, c = 13. 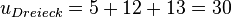 ,
, 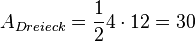
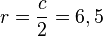 (Thaleskreis!), also ist
(Thaleskreis!), also ist 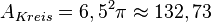
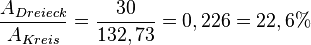
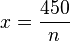 .
.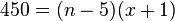 . Diese Gleichung hat nun zwei Unbekannte n und x. Wir kennen aber einen Zusammenhang zwischen n und x, nämlich
. Diese Gleichung hat nun zwei Unbekannte n und x. Wir kennen aber einen Zusammenhang zwischen n und x, nämlich 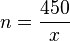 . Setzt man die letzte Gleichung für n in die Gleichung
. Setzt man die letzte Gleichung für n in die Gleichung 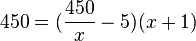 .
Die Gleichung
.
Die Gleichung 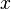 multipliziert (und dabei auf der rechten Seite die erste Klammer als
multipliziert (und dabei auf der rechten Seite die erste Klammer als 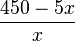 schreibt, dann fällt nämlich beim Multiplizieren mit x der Nenner weg.)
schreibt, dann fällt nämlich beim Multiplizieren mit x der Nenner weg.)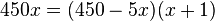
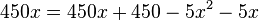
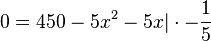
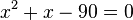 mit den zwei Lösungen
mit den zwei Lösungen 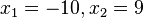 .
. 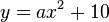 und
und 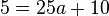 ergibt sich
ergibt sich 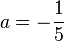 , also
, also 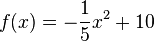
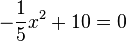 , also
, also 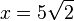 .
.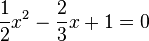
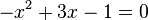
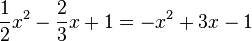
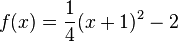 und
und