M9 Parabelgleichung ablesen und Parabel zeichnen
Ausgangspunkt unserer Überlegungen ist die Normalparabel, der Graph der Funktion 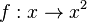 mit den eingezeichneten Punkten.
mit den eingezeichneten Punkten.
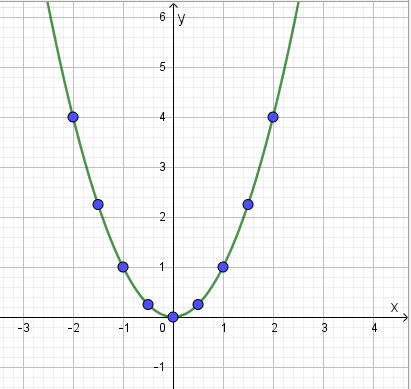
Für die Punkte hat man folgende Tabelle:
| x | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 |
| y | 4 | 2,25 | 1 | 0,25 | 0 | 0,25 | 1 | 2,25 | 4 |
Zum Zeichnen oder Ablesen geht man bei einer Parabel mit a = 1, also y = x^2 + bx + c stets vom Scheitel S, dessen Koordinaten (xS;yS) wir kennen, aus.
a = 1 bedeutet, dass die Parabel zur Normalparabel kongruent ist. Sie ist also nur um xS in x-Richtung und yS in y-Richtung verschoben.
Man kann die Parabel, die kongruent zur Normalparabel ist (a = 1) und den Scheitel S(xS;yS) hat immer wie eine Normalparabel zeichnen.
Gehe von S aus -0.5 nach links bzw. 0,5 nach rechts und von dort jeweils 0,25 nach oben.
Gehe von S aus -1 nach links bzw. 1 nach rechts und von dort jeweils 1 nach oben.
Gehe von S aus -1,5 nach links bzw. 1,5 nach rechts und von dort aus jeweils 2,25 nach oben
Gehe von S aus -2 nach links bzw. 2 nach rechts und von dort aus jeweils 4 nach oben.
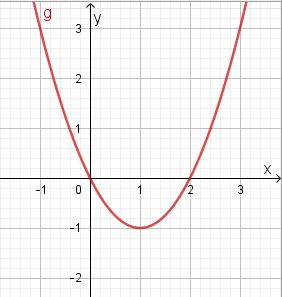
Umgekehrt kann man von einer gezeichneten Parabel die Parabelgleichung bestimmen.
Bei einer Normalparabel bestimme die Koordinaten xS und yS des Scheitels und setze sie in die Scheitelform (x - xS)2 + yS ein. Vereinfache dann den Term.
Geht man von S aus -1 nach links oder 1 nach rechts und jeweils von dort senkrecht nach oben, dann muss man 1 nach oben gehen, damit man auf die Parabel kommt.
Was ist, wenn a ≠ 1 ist?
1. Die roten Punkte haben die Koordinaten (-1;a) und (1;a).
2. Die y-Koordinaten der roten Punkte auf der Parabel y = ax2 sind jeweils a.
Stelle dazu in dem Applet a = 1, xS = 0 und yS = 0 ein. Da hat man wieder die Normalparabel. In dem Applet sind die Punkte (-1;1) und (1;1) eingezeichnet. Wenn man nun den Schieberegler für a betätigt, dann sieht man, dass aus den Punkten (-1;1) und (1;1) die Punkte (-1;a) und (1;a) werden. Die y-Koordinate wird also jeweils mit a multipliziert.
a) yP = 2, yQ = 2
b) yP = 3, yQ = 3
c) yP = -1, yQ = -1
d) yP = -2, yQ = -2
Die y-Koordinaten der Punkte U und V werden auch jeweils mit a mutipliziert.
e) A hat dann die y-Koordinate a·2,25 und B die y-Koordinate a·2,25.
Im folgenden Applet kannst du die Werte für xS, yS und a einstellen und am Graphen den Funktionsterm ablesen. Am Graph ist die Scheitelform angegeben, im Fenster eventuell der "normale" Term.
30px Merke
Für folgende Überlegungen steht das nachfolgende Applet zur Verfügung. Umgekehrt kann man für einen quadratischen Term |
Arbeitsblatt 1:
(1) Scheitel S(-2;-3) und a = 2 (die Parabel ist nach oben geöffnet, also ist a positiv; man geht von S aus 1 nach rechts und 2 nach oben), also y = 2(x + 2)2 - 3 = 2x2 + 8x + 5
(2) Scheitel S(1;-1) und a = 0,25 (bei der Normalparabel geht man 2 nach rechts und 4 nach oben, hier geht man von S aus 2 nach rechts und 1 nach oben, also 1 ist 1/4 von 4), also y = 0,25(x - 1)2 - 1 = 0,25x2 - 0,5x - 0,75
(3) Scheitel S(1;-2) und a = 0,5 (bei der Normalparabel geht man 1 nach rechts und 1 nach oben, hier geht man von S aus 1 nach rechts und 0,5 nach oben, also 0,5 ist 1/2 von 1), also y = 0,5(x - 1)2 - 2 = 0,5x2 - x - 1,5
(4) Scheitel S(-1;3) und a = -0,25 (de Parabel ist nach unten geöffnet, also ist a negativ; bei der Normalparabel geht man 2 nach rechts und 4 nach oben, hier geht man von S aus 2 nach rechts und 1 nach unten, also -1 ist -1/4 von 4), also y = -0,25(x + 1)2 +3 = -0,25x2 - 0,5x + 2,75
(5) Scheitel S(-1;2) und a = -0,5 (Parabel ist nach unten geöffnet, also ist a negativ; bei der Normalparabel geht man 2 nach rechts und 4 nach oben, hier geht man von S aus 2 nach rechts und 2 nach unten, also -2 ist -1/2 von 4), also y = -0,5(x + 1)2 + 2 = -0,5x2 - x + 1,5
(6) Scheitel S(2;4) und a = -1,5 (Parabel ist nach unten geöffnet, also ist a negativ; bei der Normalparabel geht man 1 nach rechts und 1 nach oben, hier geht man von S aus 1 nach rechts und 1,5 nach unten, also a=-1,5), also y = -1,5(x - 2)2 + 4 = -1,5x2 + 6x - 2
Die zweite Aufgabe auf dem Blatt kannst du selbst mit GeoGebra kontrollieren.
Aufgabenblatt 2:
1. Auf diesem Blatt sind nur Normalparabeln, also a = 1.
a) S(2;-9)
b) S(-1,5;-0,75)
c) S(-0,6;-2,86)
d) S(0,5;-1,5)
e) S(1,5;-3,25)
f) S(-2;-6,5)
2. Alle Parabeln sind nach oben geöffnet, also ist a = 1.
(1) S(-2;0,5), y = (x + 2)2 + 0,5 = x2 + 4x + 4,5
(2) S(-0,5;-1,5), y = (x + 0,5)2 - 1,5 = x2 - x - 1,75
(3) S(1;-2), y = (x - 1)2 - 2 = x2 - 2x - 3
(4) S(0,5;1,5), y = (x - 0,5)2 + 1,5 = x2 - x + 1,25
(5) S(2,5;1,5), y = (x - 2,5)2 + 0,5 = x2 - 5x -5,75
3. Alle Parabeln sind nach unten geöffnet, also ist a = -1.
blau: S(-2;0), y = -(x + 2)2 + 0 = -x2 - 4x - 4
rot: S(0;0); y = -x2
grün: S(0;2), y = -x2 + 2
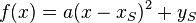 einsetzen.
einsetzen.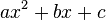 genauso gut die Parabel zeichnen.
genauso gut die Parabel zeichnen.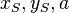 ablesen.
ablesen.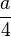 in y-Richtung. --> 2 weitere Punkte der Parabel.
in y-Richtung. --> 2 weitere Punkte der Parabel.
