Mathematische Hintergründe

Mathematisch - Informationstechnische Hintergründe Erzeugung von 3D-Bildern Weitere Ableitungen Mathematische Hintergründe

In einem digitalen Höhenmodell ist über die Landschaft ein x-y-Gitter gelegt. Als dritte Koordinate wird einem Punkt (x;y) der Ebene die Höhe h zugeordnet. Ein Datensatz, der in der Regel in einem Textfile abgelegt wird, besteht aus dem Tripel (x, y, h). Die Umsetzung in eine Höhenschichtkarte erfolgt nun einfach durch einer Zuordnung eines Farbwertes durch eine Funktion Farbe(h). 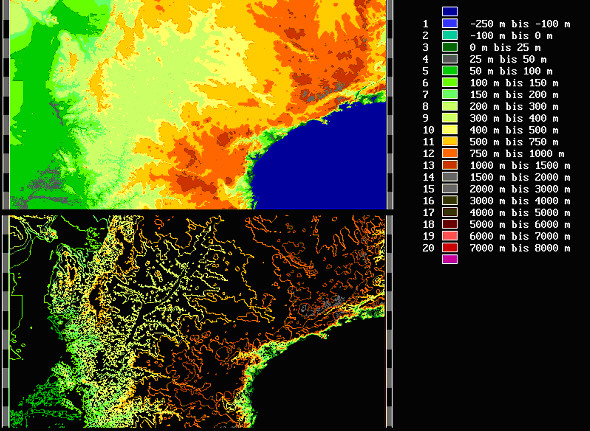Eine solche Umsetzung erfolgt am RSG anhand der GTOPO30-Daten in einem in Pascal geschriebenen Programm in einer Informatik-Neigungsgruppe Ende der 90-er Jahre: Höhenschicht- und daraus abgeleitete Höhenlinienkarte eines Teiles Südamerikas Grundlage: GTOPO30-Daten des US-Geological Survey Die Umsetzung der Höhenschichtkarte in eine Höhenlinienkarte erfolgte zeilenweise nach benachbarten Bildschirmpunkten durch Auslesen der Pixelfarbe vom Bildschirm und Abfrage, ob sich der Farbwert ändert. Bei Farbwertsänderungen wurde wieder der Bildschirmpunkt in der Farbe gesetzt, andernfalls wurde er auf schwarz gesetzt. 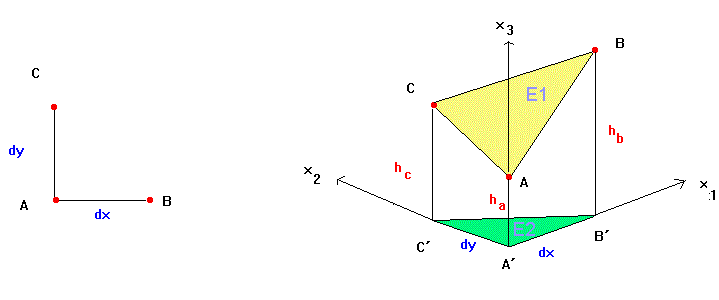Die Erzeugung von Hangneigungskarten gestaltet sich etwas schwieriger, ist aber mit den Methoden der 11. Klasse G 8 machbar: Am Beispiel einer Plattkarte sei dies erläutert: Drei "benachbarte" Datensatzpunkte, A´(Spalte, Zeile), B´(Spalte + distance, Zeile ) und C´(Spalte, Zeile - distance), bilden für einen hinreichend kleinen Wert von distance, auf die Erdkugel abgebildet annähernd ein ebenes rechtwinkliges Dreieck. An der Position A´, B´und C´ in der Datei stehen die Höhen ha, hb und hc. Der Wert für dx ist abhängig vom Wert der Variablen distance und der geographischen Breite des Datensatzpunktes auf der Erde. Der Wert dy ist dagegen lediglich abhängig vom Wert von distance. Die Geländepunkte A, B und C befinden sich auf der Höhe ha, hb und hc über NN. Ihre senkrechte Projektion in die Grundebene bilden bei A´ einen rechten Winkel. Der Abstand der Punkte B´ und C´ von A´ in der Grundebene sei mit dx bzw. dy bezeichnet. Legt man den Punkt A´ zusätzlich noch in den Ursprung des Koordinatensystems hinein, so haben die Punkte folgende Koordinaten: A(0,0,ha), B(dx,0,hb) und C(0,dy,hc) Die Hangneigung ist nichts anderes als der Schnittwinkel zwischen den beiden Ebenen E1 und E2. Diesen bestimmen wir der Einfachheit mit den Methoden der vektoriellen Geometrie. Dazu benötigen wir die Gleichungen der beiden Ebenen geeigneterweise in Normalenform. E2: x3 = 0 mit dem Normalenvektor n2 = (0, 0, 1)T Die beiden Richtungsvektoren AB und AC ergeben sich zu: AB = (dx,0,hb-ha)T bzw. AC = ( 0,dy, hc-ha)T Ein Normalenvektor der Ebene E1 sei n1 = (v1,v2,v3)T. Die skalare Multiplikation von AB bzw. AC mit n1 ergibt die beiden linearen Gleichungen: 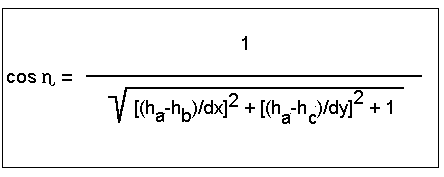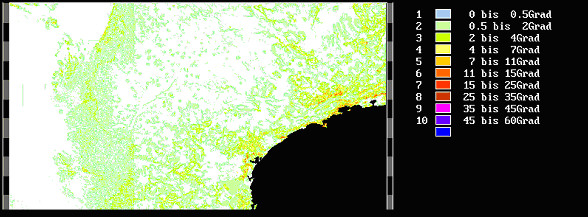(1) v1 dx + v3(hb-ha) = 0 (2) v2 dy + v3(hc-ha) = 0 Da dx und dy natürlicherweise verschieden von Null sind ergibt bei frei wählbarem v3, z.B. v3 = 1 die Lösung des Gleichungssystems: (3) v1 = (ha-hb)/dx,v2 = (ha-hc)/dy,v3 = 1 Zur Bestimmung des Schnittwinkels der beiden Ebenen muß nun noch n1 normiert, d. h. auf die Länge 1 gebracht werden.Damit ergibt sich für den Neigungswinkel des Hanges: Führt man nun für den Datensatz zeilenweise die Berechnung aus und ordnet bestimmten Neigungswinkeln eine Farbe zu, so erhält man eine Hangneigungskarte wie unten: Hangneigungskarte eines Teiles Südamerikas Grundlage: GTOPO30-Daten des US-Geological Survey Mit den Mitteln der Koordinatengeometrie kann man auch die sog. Fallrichtung bestimmen, das ist die Richtung, in die man blickt, wenn man hangabwärts schaut: Ein Normalenvektor ist n=((ha-hb)/dx,(ha-hc)/dy,1)T,seine Projektion in die x-y-Ebene ist n3=((ha-hb)/dx,(ha-hc)/dy,0)T Damit man die Fallrichtung nicht nur hinsichtlich der Orientierung, sondern auch bezüglich der Richtung richtig erhält, benötigt man stets einen vom selbst gewählten Ursprung des Koordinatensystems weg zeigenden Normalenvektors. Dies ist der Fall, wenn man von der Ebenengleichung n x = 0 die Hessesche Normalenform (HNF) bildet: (n1x1 + n2x2 + n3x3) /(- sgn(n1)sqrt(n12 + n22 +32)) = 0 Damit ist ebenfalls n3 zu korrigieren: n3*o = n3 /(- sgn(n1)sqrt(n12 + n22 +n32)) = 0 Für die Orientierung gegenüber der y-Achse gilt: sin(ß) = ((ha-hb)/dx)/(- sgn((ha-hb)/dx))sqrt(((ha-hb)/dx)2 + ((ha-hc)/dy)2 +1) cos(ß) = ((ha-hc)/dy)/(- sgn((ha-hb)/dx))sqrt(((ha-hb)/dx)2 + ((ha-hc)/dy)2 +1) Aus diesen beiden Werten bestimmt man dann, von Nord aus gegen die Uhrzeigersinn gerechnet die Fallrichtung, d. h. die Exposition der Hänge. Zeilenweise Umsetzung in den Daten ergibt eine Expositionskarte. In Wirklichkeit ist das Problem der Bestimmung der Hangneigung viel komplexer, da die Punkte eine bestimmte Distanz aufweisen, die das Relief dazwischen unberücksichtigt lassen. Kann man einem Landvermesser noch trauen, der mit der Auswahl seiner Punkte "sinnvoll" umgeht, so ist dies bei automatischer Vermessung per Satellit oder Laserscanning vielmehr eine Frage der "Rauhheit" des Geländes, da die gescannten Punkte unabhängig vom tatsächlichen Relief gesetzt sind. Hier spielen Fragen der fraktalen Geometrie, aber auch der komplexen Funktionen ein Rolle. Dazu demnächst an dieser Stelle Näheres. Informationen zu digitalen Geländemodellen bei der Bayerischen Vermessungsverwaltung

Behördeninformationen Info zum Rahmenvertrag Internetauftritt der Bayerischen Vermessungsverwaltung mit dem Datenangebot Internetauftritt des Vermessungsamtes Ansbach Frei zugänglicher Bayernviewer Software Surfer Demoversion für Digitale Geländemodelle Frei zugängliche Daten GTOPO30 Weitere Produkte von USGS