Ph10-Wellen
Du hast kennengelernt, wie Wellen entstehen und was eine Welle ist.
Inhaltsverzeichnis |
Wiederholung
1. Eine Welle ist eine Schwingung, die von vielen Teilchen periodisch hintereinander ausgeführt wird und sich räumlich ausbreitet.
2. Wellen transportieren keine Materie, sondern Energie.
Wenn du im Meer auf dem Wasser liegst machst du durch die Wasserwellen eine Auf- und Abbewegung, bewegst dich aber nicht von deinem Ort. D.h. Wellen transportieren keine Materie.
Dass Energie durch Wellen übertragen wird, sieht du an Höhlen, Löchern in Felsen, ...., die durch die Brandung erzeugt werden. D.h. Wellen transportieren Energie, die z.B. Verformungen hervorrufen.
3. Wellen werden durch Größen wie Frequenz f, Schwingungsdauer T Amplitude A, Kreisfrequenz 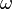 (das sind auch die Größen der Erregerschwingung, die sich in der Welle fortsetzen), Ausbreitungsgeschwindigkeit c und Wellenlänge
(das sind auch die Größen der Erregerschwingung, die sich in der Welle fortsetzen), Ausbreitungsgeschwindigkeit c und Wellenlänge 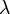 .
.
30px Merke
Eine Welle ist eine Schwingung, die sich periodisch räumlich und zeitlich ausbreitet. |
Reflexion von Wellen - stehende Welle
In diesem Video mit der Wellenmaschine wird die Entstehung einer stehenden Welle erklärt. Eine Wellenmaschine erzeugt und demonstriert die Ausbreitung von Wellen.
1. Eine stehende Welle entsteht durch Überlagerung zweier gegeneinander laufender Wellen gleicher Frequenz.
2. Die gegenlaufende Welle wird durch Reflexion am rechten Ende der Wellenmaschine erzeugt.
2. Loses Ende: frei liegendes Seil, am rechten Ende nicht eingespannte Wellenmaschine, Wasserwelle, offene Orgelpfeife ...
Festes Ende: am rechten Ende eingespanntes oder fest gehaltenes Seil, am rechten Ende fest gemachte Wellenmaschine, geschlossene Orgelpfeife, Seilspringen ...
4. Bei der Reflexion am losen Ende kann der Wellenberg das letzte Molekül auslenken, welches dann den Wellenberg wieder zurück gehen lässt.
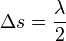 .
.
|
Merke:
1. Kommt eine Welle bei ihrer Ausbreitung an ein loses Ende des Ausbreitungsmediums, dann wird die Welle reflektiert. Die reflektierte Welle läuft in die Gegenrichtung zurück und hat gleiche Amplitude, gleiche Frequenz und gleiche Wellenlänge wie die ankommende Welle. Ankommende und reflektierte Welle haben keinen Gangunterschied. Bei der Reflexion entsteht keine Phasenverschiebung. |
Die Reflexion am losen und festen Ende und das Entstehen einer stehenden Welle ist im Rest des Videos von Aufgabe 3 ganz ausführlich erklärt. Wer will kann sich das Video gerne zu Ende anschauen.
Wie entstehen stehende Wellen. Was passiert, wenn zwei gegeneinanderlaufende Wellen gleicher Frequenz aufeinander treffen?
Treffen zwei gegeneinanderlaufende Störungen (Wellen) aufeinander so überlagern sie sich an diesem Ort.
An diesem Ort addieren sich ihre Amplituden und ergeben dort eine neue Schwingung, deren Auslenkung sich durch die Addition der Auslenkungen der einzelnen Störungen (Wellen) ergibt.
Die Überlagerung der zwei Wellen an einem Ort kann man durch die Schwingungen für diesen Ortspunkt darstellen.
An einem Ort wird der Punkt durch eine Welle zu einer Sinusschwingung (grün) angeregt. Gleichzeitig kommt an diesem Ort eine zweite Welle an, die den Punkt auch zu einer Sinusschwingung (rot) anregt. Die Summe der beiden Schwingungen ist die dargestellte blaue Schwingung, die durch Addition der Einzelschwingungen entsteht.
Mit dem Schieberegler kannst du die zweite Schwingung verändern, so dass der durch sie verursache Schwingungszustands des Ortspunktes nicht mehr synchron zur ersten grünen Schwingung ist, sondern um  phasenverschoben.
phasenverschoben.
1. Die blaue Kurve entsteht durch Addition der grünen und roten Kurve. Dazu werden zu jedem Zeitpunkt T die Auslenkungen ygrün und yrot addiert, es ist also yblau = ygrün + yrot.
2. Bei 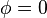 ist die Amplitude der blauen Schwingung am größten. Vergrößert man
ist die Amplitude der blauen Schwingung am größten. Vergrößert man 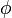 , dann wird die Amplitude der blauen Schwingung kleiner und verschiebt sich. Bei
, dann wird die Amplitude der blauen Schwingung kleiner und verschiebt sich. Bei 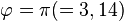 ist die Amplitude der blauen Schwingung 0.
ist die Amplitude der blauen Schwingung 0.
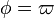 ist, dann sind die grüne und die rote Schwingung gegenphasig, ihre Auslenkungen heben sich gegenseitig auf und die Summe (blau) ist 0.
ist, dann sind die grüne und die rote Schwingung gegenphasig, ihre Auslenkungen heben sich gegenseitig auf und die Summe (blau) ist 0.
30px Merke
An einem Ort überlagern sich zwei Wellen so, dass sie den Ortspunkt zu einer Schwingung anregen, die sich als Addition der Einzelschwingungen der einzelen Wellen ergibt. |
Knoten und Bäuche sieht man sehr schön bei der Schwingung des Federwurms und der Gummischnur.
In den folgenden Videos wird die Tonerzeugung bei Musikinstrumenten erklärt.
| Flöte | Orgel | Gitarre, Geige |
Zum Schluss noch ein Video von Schülern einer 10. Klasse
Interferenz von Wellen
30px Versuch
Du hast an deinem PC zwei Lautsprecher? Die Lage der Lautsprecher kannst du verändern? |
3. Beim entlang gehen hört man immer denselben Ton, dessen Lautstärke allerdings immer wieder zu- und abnimmt.
4. Stellt man die Lautsprecher näher zusammen oder weiter auseinander, dann werden die Abstände lauter - leiser länger oder kürzer.
5. Auch bei anderen Frequenzen stellt man fest, dass beim Entlanggehen die Lautstärke des Tons zu- und abnimmt.
Also bei mir hat dieser Versuch so funktioniert. Ob er bei dir auch funktioniert hängt eventuell von deinen Lautsprechern ab, den Raumgegebenheiten, ....
Ich mache normal diesen Versuch immer an einem Whiteboard, an dem Lautsprecher befestigt sind. Ihr lauft dann im Abstand 2 - 5m parallel zum Whiteboard entlang und man hört dort sehr gut das lauter- und Leiserwerden des eingestellten Tons.
Wie kommen diese Lautstärkeschwankungen zustande?
An dem Ort an dem du stehst kommen zwei Wellen an. Von jedem Lautsprecher eine. Je nachdem wie sie bei dir ankommen kann folgendes passieren.
30px Merke
Zwei Wellen überlagern sich in einem Punkt so, dass sich ihre Auslenkungen addieren. Die Überlagerung zweier oder mehrerer Wellen heißt Interferenz. |
Die Interferenz zweier Kreiswellen kann man auch schön an Wasserwellen beobachten.
Um zu verstehen wie die Interferenzbilder entstehen, betrachten wir zwei Wellen, die sich in einem Punkt A treffen.
Wir betrachten also in einem Punkt zwei ankommende Wellen und unterscheiden drei Fälle.
1. Die zwei Wellen kommen gleichphasig an, d.h. an deinem Ort kommen zwei Sinuswellen im jeweils gleichen Zustand an.
In diesem Applet kommt eine rote und eine grüne Sinusschwingung - die beiden Wellen liegen praktisch in dem Punkt aufeinander - an und überlagern sich im Punkt A zu der blauen Schwingung. Mit Hilfe des Schiebereglers kannst du die Wellen fortschreiten lassen und siehst die überlagerte Welle bzw. die Schwingung am Punkt A, die sich dann weiter fortsetzt.
Man sieht, dass am Punkt A sich die beiden Wellen so überlagern,sich ihre Auslenkungen addieren und die Summenwelle maximale Amplitude hat. Man spricht von konstruktiver Interferenz.
Da an diesem Ort die Wellenbewegung maximal ist, spricht man von einem Interferenmaximum.
2. Die zwei Wellen kommen gegenphasig an, d.h. an deinem Ort kommt eine Sinuswelle und eine Minus-Sinuswelle an. Die zwei Wellen haben Gangunterschied  bzw. Phasenunterschied
bzw. Phasenunterschied  .
.
Man sieht, dass die zwei Wellen gegenphasig ankommen. Auf jeden "positiven" Bauch der einen Welle kommt ein "negativer" Bauch der anderen Welle. Die Überlagerungswelle zeigt keinen Ausschlag. Ihre Amplitude ist 0. Man spricht von destuktiver Interferenz.
Dan an diesem Ort die Wellenbewegung Null, also minimal ist, spricht man von einem Interferenzminimum.
3. Kommen die Wellen irgendwie bei dir an, dann überlagern sie sich auch zu einer Interferenzwelle.
Man sieht, dass sich eine Welle ergibt, deren Amplitude kleiner als bei der konstruktiven Interferenz ist.
1. Konstuktive Interferenz entsteht in einem Punkt, wenn zwei Wellen gleichphasig ankommen. "Positiver" Wellenberg trifft auf "positiven" Wellenberg und T/2 später trifft "negativer" Wellenberg auf "negativen" Wellenberg. Die Überlagerung erfolgt durch die Addition der gleichphasigen Auslenkungen.
Destuktiver Interferenz entsteht in einem Punkt, wenn zwei Wellen gegenphasig ankommen. Ein "positiver" Wellenberg trifft auf einen "negativen" Wellenberg und T/2 später trifft ein "negativer" Wellenberg auf einen "positven" Wellenberg. Die beiden Auslenkungen der einzelnen Wellen heben sich auf und die Überlagerungswelle hat dort keine Auslenkung.
2. Bei konstruktiver Interferenz schwingen die Wellen gleichphasig. Ihr Gangunterschied 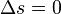 . Er kann aber auch ein Vielfaches der Wellenlänge
. Er kann aber auch ein Vielfaches der Wellenlänge 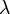 sein, also
sein, also 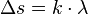 mit
mit 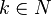 .
.
Bei destruktiver Interferenz schwingen die Wellen gegenphasig. Ihr Gangunterschied 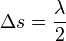 . Er kann aber auch ein Vielfaches der Wellenlänge
. Er kann aber auch ein Vielfaches der Wellenlänge 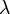 weiter sein, also
weiter sein, also 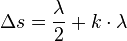 mit
mit 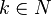 .
.
3. Bei der Interferenz von Wasserwellen gibt es Stellen, wo die Wasseroberfläche ruhig ist, dort löschen sich die zwei Kreiswellen aus, man hat dort destruktive Interferenz.
Andere Stellen bewegen sich auf und auf, dort hat man konstruktive Interferenz. Die zwei Wasserwellen überlagern sich, so dass sie sich verstärken.
4. Verminderung von Geräuschen in Autos, bei Kopfhörern
30px Versuch
Führe auf dieser Seite das Simulationsexperiment durch. Wähler hierzu im Menü Interferenz aus. |
1. Man erkennt im Interferenzbild Stellen an denen sich hell und dunkel abwechselt und Stellen, die nur gleichbleibend bläulich erscheinen.
2. Die hellen und dunklen Stellen entstehen, indem am das Wasser von unten bestrahlt. Ist ein Wellenberg da, dann hat man viel Wasser und das Licht kommt nicht durch, es ist dunkel. Hat man ein Wellental, dann ist wenig Wasser da, das Licht kommt leicht durch, es ist hell. Bei den gleichbleibend bläulichen Stellen hat man immer gleich viel Wasser und das Licht kommt immer gleich durch.
3. Auf der Mittelsenkrechten zu den beiden Wassertropfen haben beide Wellen stets den gleichen Weg. Sie überlagern sich dort konstruktiv, also wechseln sich dort Wellenberg und Wellentäler ab, was zum Wechsel von dunkel und hell führt.
 .
.
Der Doppelspaltversuch
Bei Wasserwellen kann man mit zwei Erregern synchron zwei Wellen erzeugen.
Bei Licht hat man Probleme damit. Man hat bei Licht nie zwei Erreger, die genau synchron Wellen aussenden. Man kann aber zwei synchrone Wellen erzeugen, indem man eine ebene Wellenfront auf einen Doppelspalt sendet. Sind die Spalte des Doppelspalts eng genug dann man nach ihnen zwei Kreiswellen, die sich überlagern.
Das Phänomen der Interfenz zweier Wellen tritt also auch bei Lichtwellen auf und zeigt an der Projektionsfläche ein Interferenzmuster.
Wie entsteht dieses Interferenzmuster?
Egal ob Wasser- oder Lichtwellen man sieht bei beiden Interfenzen das gleiche Interferenzmuster. Bei Wasserwellen nimmt man einfach eine parallele Ebene zu den Erregern der zwei Wasserwellen und sieht dort Punkte wo sich hell und dunkel abwechseln und graue Bereiche. Beim Laser entsprechen die roten Punkte den sich abwechselnden hell-dunkel Punkten des Wassers und die dunklen Punkte den grauen Bereichen.
Im folgenden Bild ist ein Doppelspalt zu sehen von dem aus zwei Wellen ausgehen.
An dem Punkt an dem sich die zwei Wellen treffen haben sie einen Gangunterschied 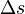 .
.
Ist der Gangunterschied ein Vielfaches von 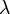 , also
, also 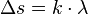 dann hat man dort konstruktive Interferenz und die Wellen verstärken sich. Man hat dort ein Maximum.
dann hat man dort konstruktive Interferenz und die Wellen verstärken sich. Man hat dort ein Maximum.
Ist der Gangunterschied  und ein Vielfaches von
und ein Vielfaches von 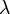 , also
, also 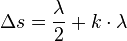 dann hat man dort destruktive Interferenz und die Wellen löschen sich aus. Man hat dort ein Minimum.
dann hat man dort destruktive Interferenz und die Wellen löschen sich aus. Man hat dort ein Minimum.
a) Bei Wasserwellen erkennt man Maxima durch auf- und ab-Bewegung des Wassers und Minima durch ruhige Wasserstellen.
|
Merke:
Nach dem Doppelspalt ergeben sich Maxima durch konstruktive Interferenz. Nach dem Doppelspalt ergeben sich Minima durch destruktive Interferenz. |
Wasserwellen haben in unseren Versuchen Wellenlängen im Bereich cm. Ansonsten können sie auch auch kleine und sehr viel größere Wellenlängen haben. Der Abstand der Erreger ist auch in diesem Bereich. Bei Lichtwellen sind die Wellenlängen von 400nm bis 700nm, also sehr viel kleiner (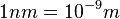 ). Der Abstand der beiden Doppelspalte muss auch in diesem Bereich sein. Dagegen ist der Abstand des Schirms, auf dem man das Interferenzbild betrachtet sehr viel größer als die Wellenlänge und der Abstand der Doppelspalte.
). Der Abstand der beiden Doppelspalte muss auch in diesem Bereich sein. Dagegen ist der Abstand des Schirms, auf dem man das Interferenzbild betrachtet sehr viel größer als die Wellenlänge und der Abstand der Doppelspalte.
Im folgenden Bild ist diese Situation für Lichtwellen dargestellt.
Im Versuch ist d ca. 1m und x sind ein paar mm. Also ist d>>x, d.h. d ist sehr groß gegenüber x. Dann kann man die Kleinwinkelnäherung, die du beim Fadenpendel kennengelernt hast, anwenden. Es ist dann 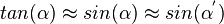 und man kommt dann auf die Beziehung für den Gangunterschied
und man kommt dann auf die Beziehung für den Gangunterschied 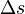
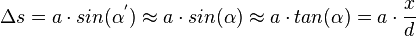
Im Versuch kennt man eventuell vom Hersteller den Abstand a der Doppelspalte. Den Abstand d des Schirm zum Doppelspalt kann man messen, ebenso wie den Abstand x der Maxima (helle Punkte) auf dem Schirm. Für das 1. Maximum gilt 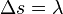 . Dann kann man damit die Wellenlänge
. Dann kann man damit die Wellenlänge 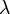 bestimmen. Es ist dann
bestimmen. Es ist dann 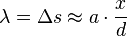 . Oder wenn man die Wellenlänge kennt, kann man z.B. a bestimmen.
. Oder wenn man die Wellenlänge kennt, kann man z.B. a bestimmen.
In diesem Video
wird erklärt wie man mit Hilfe des Interferenzbildes der Interferenz am Doppelspalt die Wellenlänge eines Laserlichts bestimmen kann.
30px Versuch
Schaue dir den Doppelspaltversuch auf dieser Seite an. |
Auf dieser Seite sind die Überlegungen zum Doppelspalt nochmals ausführlich dargestellt.

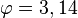 ist?
ist?

