Ph10 Zentripetalkraft
Damit ein Körper sich auf einer Kreisbahn bewegt muss eine Kraft wirken. Vom Trägheitssatz wissen wir, dass ein Körper, auf den keine Kraft wirkt sich geradlinig weiterbewegt oder in Ruhe ist. Da eine Kreisbahn nicht geradlinig ist, muss also bei einer Kreisbewegung eine Kraft wirken. Diese Kraft ist stets zum Drehzentrum gerichtet und von konstantem Betrag.
Diese Kraft ist etwa bei einem Karussell die Zugkraft eines Seils oder einer Stange zwischen dem Drehzentrum und dem Körper, oder bei einer Kurvenfahrt eines Fahrrads oder Autos die Haftreibung zwischen den Reifen und der Straße.
|
Merke:
Die Kraft, die einen Körper auf eine Kreisbahn zwingt, ist die Zentripetalkraft FZ. Die Kraft siehst du in folgendem Video für verschiedene Drehgeschwindigkeiten. |
30px Versuch
Die Zentripetalkraft merkst du, wenn du eine Kurve läufst. 1. Versuche in gerader Haltung (du bist gerade und senkrecht zum Boden) eine Kurve zu gehen. Gehe zuerst ganz langsam und werde dann schneller. Was stellst du fest? 2. Zeichne auf der Straße einen Kreis mit Radius 2m und renne entlang dieses Kreises. Was kannst du über deine Haltung aussagen? |
1. In gerader Haltung kann man nur ganz langsam einen Kreis gehen. Will man schneller gehen muss man seine Körperhaltung zum Kreismittelpunkt neigen.
2. Wenn man entlang eines Kreises rennt, muss mann sich nach innen neigen.
30px Versuch
|
|
Merke:
Bewegt sich ein Körper auf einer Kreisbahn vom Radius r mit a) der Bahngeschwindigkeit v, dann ist die Zentripetalkraft b) mit der Winkelgeschwindigkeit |
30px Versuch
Verifiziere die zwei Kraftformeln für die Zentripetalkraft mit den Applets auf der Seite von Leifiphysik. Für die 1. Formel Auf dieser Seite von Leifiphysik ist ein Versuch dargestellt, mit dem man die Formeln experimentell bestimmen kann. |
Auf Volksfesten hast du schon Kreisbewegungen selbst mit gemacht. Und da hast du sicher stets eine auf dich wirkende Kraft gespürt, die nach außen wirkt. Unsere Zentripetalkraft wirkt aber nach innen? Wie passt das zusammen?
Das hängt damit zusammen, dass wir unsere Versuche bisher immer von außen angesehen haben und damit ein Körper sich auf einer Kreisbahn bewegt, muss die Zentripetalkraft nach innen wirken. Wenn du aber selbst der Körper bist, spürst du eine Kraft nach außen, die sogenannte Zentrifugalkraft. Wir haben aber hier zwei verschiedenen Versuche. Einmal beobachten wir von außen den Versuch, beim anderen Versuch sind wir daran direkt beteiligt. Wir sind also in verschiedenen Bezugssystemen. Dies hat zur Folge, dass wir die wirkende Kraft anders wahrnehmen.
Dieser Sachverhalt wird auf der Seite von Leifiphysik nochmals erklärt. Die Wirkung der Zentrifugalkraft siehst du auch in diesem Video. Die zwei Kugeln werden nach außen gehoben. Das ist die Zentrifugalkraft.
Allerdings sehen wir als Betrachter von außen, dass die Kugeln nicht wegfliegen, also durch eine Kraft auf der Kreisbahn gehalten werden. Das ist die Zentripetalkraft.
30px Merke
Betrchtet man ein rotierendes System von außen, dann sieht man die Wirkung der Zentripetalkraft. Ist man im rotierenden System, so merkt man selbst die Zentrifugalkraft. |
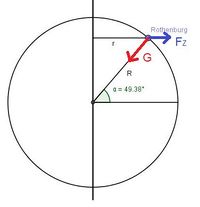
a) Durch die Erdrotation bewegen wir uns in Rothenburg auf einem Kreis mit Radius r um die Rotationsachse.
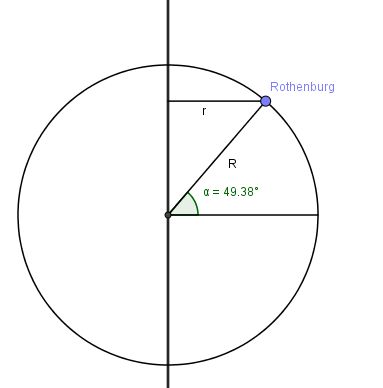
Der Radius r ist durch den Erdradius R = 6370km und dem Breitengrad \alpha = 49,38^o bestimmt. Es ist r = R\cdot cos(\alpha) = 6370 km \cdot cos(49,38^o)=4147km.
In T = 24h dreht sich die Erde einmal um ihre Achse.
Die Zentripetalkraft 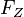 ist
ist 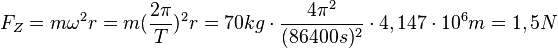
b) Die Zentrifugalkraft hat den gleichen Betrag wie die Zentripetalkraft. Die Zentrifugalkraft auf die Person ist also 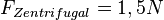 und damit ist sie sehr viel kleiner als die Gewichtskraft
und damit ist sie sehr viel kleiner als die Gewichtskraft 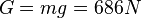 der Person. Es ist
der Person. Es ist 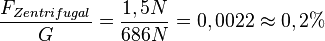 .
.
c) Die Zentripetalkraft bringt die Gewichtskraft (Erdanziehungskraft) der Person auf. Die Erdanziehungskraft wirkt wie ein Seil, das die Person zum Erdmittelpunkt zieht.
Damit die Person schwebt muss die Bedingung 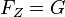 erfüllt sein, die Zentripetalkraft ist genauso groß wie die Erdanziehungskraft.
erfüllt sein, die Zentripetalkraft ist genauso groß wie die Erdanziehungskraft.
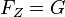
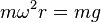
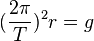
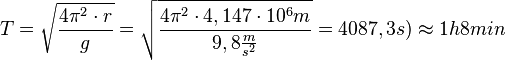
Hier wurde nicht berücksichtigt, dass die Richtungen der Gewichtskraft G und der Zentripetalkraft FZ unterschiedlich sind. G ist in Richtung Erdmittelpunkt, FZ geht radial (senkrecht zur Rotationsachse) nach außen.
a) ---
b) 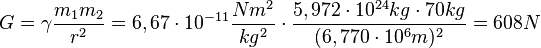
Die Gewichtskraft GISS des Astronauten in der ISS ist fast genauso groß wie die Gewichtskraft GErde des Astronauten auf der Erde. Sie ist GISS=0,89 GErde , also ist der Astronaut nicht schwerelos.
c) Wie kommt nun die im Video gesehene Schwerelosigkeit zustande?
Man berechnet die Zentripetalkraft 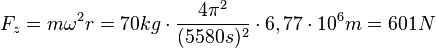
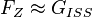 . Die Erdanziehungskraft wird fast vollständig für die Zentripetalkraft aufgebraucht. Daher hat man den Eindruck, dass die Astronauten und Gegenstände in der ISS schwerelos sind.
. Die Erdanziehungskraft wird fast vollständig für die Zentripetalkraft aufgebraucht. Daher hat man den Eindruck, dass die Astronauten und Gegenstände in der ISS schwerelos sind.
1. Die Zentripetalkraft hält dich auf der Kreisbahn. Diese Kraft wird durch die Haftreibungskraft der Unterlage auf dich aufgebracht. Du kennst bei unterschiedlichen Wetterbedingungen (trockene Straße im Sommer, eisige Straße im Winter, dass da die Haftkraft verschieden groß sein kann. Im Sommer ist sie auf trockener Straße größer, im Winter auf eisiger Straße kleiner.

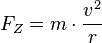 .
.
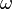 , dann ist die Zentripetalkraft
, dann ist die Zentripetalkraft 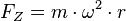 .
.
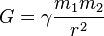 , dabei ist
, dabei ist 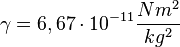 die Gravitationskonstante,
die Gravitationskonstante, 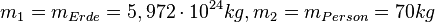 und
und  ist der Abstand zum Erdmittelpunkt,
ist der Abstand zum Erdmittelpunkt, 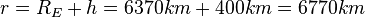 .
.
