Ph9 Bewegungen mit konstanter Beschleunigung
30px Merke
Die Formeln für eine Bewegung mit konstanter Beschleunigung a sind:
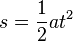 , dabei ist v die Geschwindigkeit des Körpers und s der bei der Bewegung zurückgelegte Weg.
|
72/2
a) Die Aussage "Ich bin 3m vom Bach entfernt!" ist relativ nichtssagend, da man nicht weiß wie schnell Theo fährt und wie er zum Bach fährt.
Die Aussage "Ich fahre mit 20km/h auf den Bach zu!" ist relativ gefährlich, da er mit 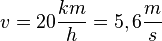 zum Bach hin fährt. Er legt also in 1s über 5m zurück. Da ist er ganz schnell "im Bach".
zum Bach hin fährt. Er legt also in 1s über 5m zurück. Da ist er ganz schnell "im Bach".
Die Aussage "Ich bin noch 10m vom Bach entfernt und fahre mit 15 km/h auf den Bach zu!" lässt erwarten, dass nichts passiert, da er mit 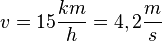 auf den Bach zufährt. Er hat also noch über 2s Zeit zum Bremsen.
auf den Bach zufährt. Er hat also noch über 2s Zeit zum Bremsen.
b) "Ich fahre in den Bach!"
72/4
a) Die Beschleunigungsarbeit ist W = Fs, also W = 4·311kN·3km=3732MJ.
Nach 3km ist idealerweise die gesamte Beschleunigungsarbeit in Bewegungsenergie umgewandet, es ist dann Ekin=3732MJ.
Die Geschwindigkeit, die er damit erreicht ist 
b) Wenn die Abhebegeschwindigkeit 260 km/h ist, dann ist die Geschwindigkeit, die 35% darüber liegt v = 351 km/h = 97,5 m/s.
Die Bewegungsenergie, die der A380 dabei hat ist 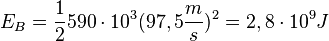 .
.
Beschleunigungsarbeit W erzeugt diese Bewegungsenergie. Bei konstanter Schubkraft ist W = Fs, also W = EB und 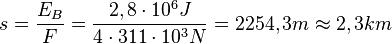 .
.
c) Mit deen Energiebetrachtungen kann man die Zeit bis zum Abheben nicht vorhersagen. Die Zeit t kam in keiner Rechnung vor und wurde auch nicht benötigt.
Macht man die Berechnung von b) mit den Bewegungsgleichungen, dann kommt die Zeit t vor.
Die Beschleunigung a ist nach dem 2. Newtonschen Gesetz F = ma gleich 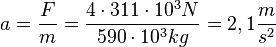 .
.
Mit der zweiten Bewegungsgleichung v = at erhält man die Zeit t mit 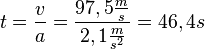 .
.
Mit der dritten Bewegungsgleichung 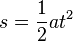 erhält man
erhält man 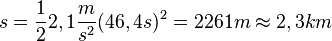
Ein ICE fährt mit einer Geschwindigkeit 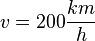 durch einen Bahnhof.
durch einen Bahnhof.
Danach beschleunigt er mit der Beschleunigung 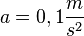 wieder auf
wieder auf 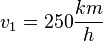 .
.
Welche Wegstrecke s legt er dabei zurück?
Dieses Problem können wir mit den Bewegungsgleichungen, wie sie oben stehen nicht lösen.
Wir können aber die Zeit 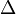 t , die der Beschleunigungsvorgang dauert berechnen. Löst man die Gleichung der Beschleunigung
t , die der Beschleunigungsvorgang dauert berechnen. Löst man die Gleichung der Beschleunigung 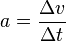 nach
nach 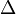 t auf, so erhält man
t auf, so erhält man 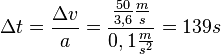 .
.
Nun stellen wir folgende Überlegung an und führen die Durchschnittsgeschwindigkeit ein.
Die Beschleunigung a eines Körpers bewirkt eine Geschwindigkeitsänderung  v in der Beschleunigungszeit
v in der Beschleunigungszeit  t. Es ist
t. Es ist 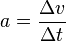 . Im tv-Diagramm wird eine Bewegung mit konstanter Beschleunigung als Gerade dargestellt.
. Im tv-Diagramm wird eine Bewegung mit konstanter Beschleunigung als Gerade dargestellt.
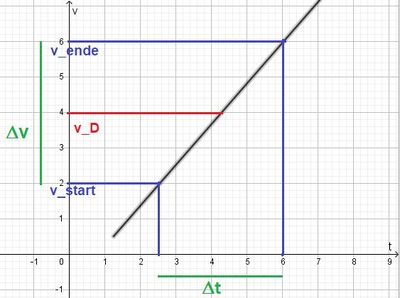
Hat zu Beginn der Beschleunigung ein Körper die Geschwindigkeit vstart und am Ende des Beschleunigungsvorgangs vende, dann ist seine Durchschnittsgeschwindigkeit vD der Mittelwert von Start- und Endgeschwindigkeit. Es ist also  .
.
30px Merke
Die Durchschnittsgeschwindigkeit |
Gehen wir nun zurück zu unserem ICE. Da wir Anfangs- und Endgeschwindigkeit kennen ist für den Beschleunigungsvorgang des ICE die Durchschnittsgeschwindigkeit des ICE 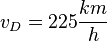 . Das ist die konstante Geschwindigkeit, mit der der ICE in der gleichen Zeit dieselbe Strecke zurücklegt. Das ist also eine Bewegung mit konstanter Geschwindigkeit und da können wir die Gleichung
. Das ist die konstante Geschwindigkeit, mit der der ICE in der gleichen Zeit dieselbe Strecke zurücklegt. Das ist also eine Bewegung mit konstanter Geschwindigkeit und da können wir die Gleichung 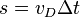 verwenden. Es ist damit
verwenden. Es ist damit 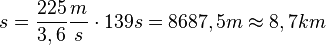 .
.
Also legt der ICE während des Beschleunigungsvorgangs knapp 9km zurück.
Es geht hier um einen Bremsvorgang, also ist die Beschleunigung a negativ.
Aus dem ersten Absatz kann man entnehmen, dass das Schiff bei einer Länge von 397m nach 15·397m = 5955m ≈ 6km zum Stehen kommen muss.
Bei volle Fahrt hat das Schiff die Geschwindigkeit 27 Knoten, das ist 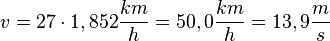 .
.
a) Die Bremskraft ist F = m·a.
Lösung mit EES: Die Bewegungsenergie wird durch Bremsarbeit vernichtet. 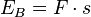 , also
, also 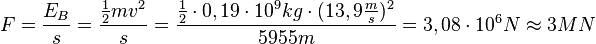 .
.
b) Nun ist die Bremskraft 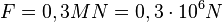 . Dann ist die Abbremsbeschleunigung
. Dann ist die Abbremsbeschleunigung 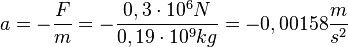 .
.
Mit 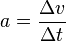 kann man nun die Zeit für den Bremsvorgang
kann man nun die Zeit für den Bremsvorgang 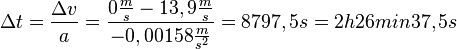
Welchen Weg legt bei diesem Bremsvorgang das Schiff zurück?
Am besten rechnet man hier von hinten. Man beschleunigt mit 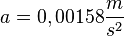 in der Zeit
in der Zeit 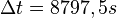 von
von 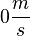 auf
auf 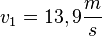 . Also ist
. Also ist 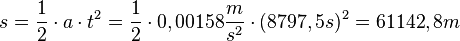 .
.
Der Bremsweg ist also über 61 km lang.
c) Nun wird das Schiff mit einer Kraft F = 150kN von 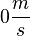 auf
auf 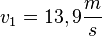 beschleunigt. Die Beschleunigung a ist
beschleunigt. Die Beschleunigung a ist 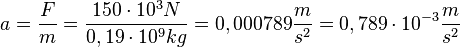 und damit ist
und damit ist 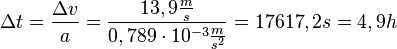 . Der Beschleunigungsvorgang dauert fast 5 Stunden.
. Der Beschleunigungsvorgang dauert fast 5 Stunden.
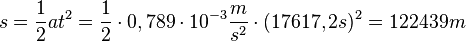 zurück, also fast 123km.
zurück, also fast 123km.
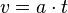 oder
oder 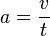
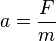 .
.
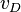 eines in der Zeit
eines in der Zeit 
