| Arbeiten mit dem CASIO Class-Pad
|

|
Zum Bearbeiten dieses Kurses benötigst Du:
|
Gliederung
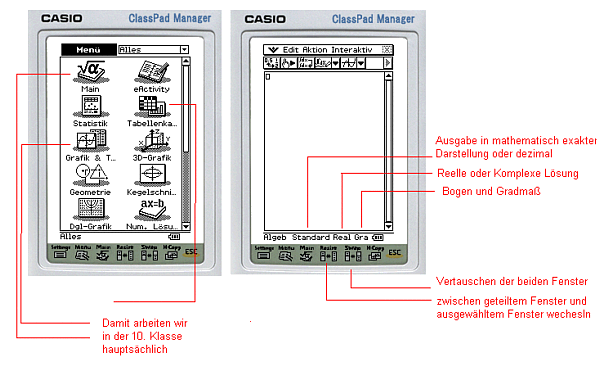
Lektion 1 - Gleichungen, Ungleichungen lösen, Funktionen zeichnen
Kurzinfos:
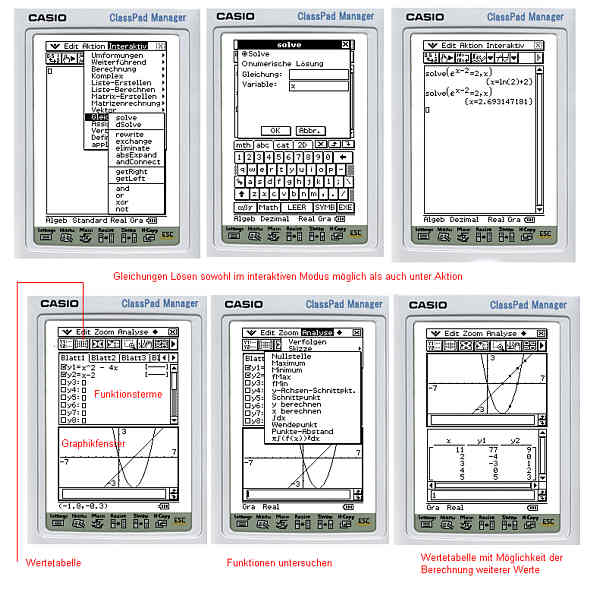
Das unten verlinkte Arbeitsblatt ergänzt die Unterrichtsinhalte vom 3.3.2011 in der Klasse 10 b und wiederholt sie.
|
Arbeitsaufgaben
- Drucke Dir das Arbeitsblatt aus und lies es Dir aufmerksam durch.
- Löse anschließend die hier eingestellten Aufgaben als Übungsbeispiele sowohl konventionell als auch mit dem ClassPad.
Datei:Ha1.GIF
- Hausaufgabe auf Donnerstag, 17. März 2011:
- Gegeben sind die Funktionen y = x^2 - 2x -7 und y = 3x - 5
- Zeichnen Sie die beiden in das Funktionenfenster des CASIO ein und bestimmen
- Sie sowohl rechnerisch, als auch graphisch bzw. mit dem CLASSPAD
- a) Nullstellen der Funktionen
- b) Schnittstellen der Funktionen und
- c)Lösen Sie die Ungleichung x^2-2x-7 > 3x-5
- Hausaufgabe auf Montag, 21. März 2011:
- Versuchen Sie die Aufgaben der 2. Schulaufgabe nur mit dem CLASSPAD zu lösen.
Hier kann die Datei der 2. Schulaufgabe heruntergeladen werden: Datei:S2-10b.pdf
Hinweis: teilweise sind dazu Kenntnisse aus Lektion 2 notwendig
|
Um Ungleichungen lösen zu können muss der CASIO-ClassPad im Real-Modus laufen.
Das hängt damit zusammen, dass in der Menge der Komplexen Zahlen keine ">"-Relation bzw. "<"-Relation sinnvoll definierbar ist.
Da im G8 keine komplexen Zahlen behandelt werden verändert man unter Settings die entsprechende Einstellung.
|
Arbeitsaufgaben
Löse folgende Ungleichungen schriftlich und mit dem ClassPad:
|
Lektion 2 - Terme vereinfachen - Terme faktorisieren
|
'Arbeitsaufgaben:
|
Die Befehle simplify, factor, rfactor, factorout
Beispiel: Gegeben ist y = x^3 - 2 x + 1;
1. Bestimme die Nullstellen:
- Solve(x^3 - 2 x + 1);
2. Zerlege in Faktoren:
- Mit dem Befehl Factor(x^3 - 2 x + 1) erhältman (x-1)(x^2-x+1)
- Mit dem Befehl rFactor(x^3 - 2 x + 1) erhält man die gewünschte Darstellung in Linearfaktoren mit Wurzeln)
3. Bestimme mittels des Verfahrens der Polynomdivision:
- (x^3-2x + 1):(x-1)
- Mit Simplify((x^3-2x + 1):(x-1)) erhält man x^2-2x+1
Lektion 3 - Bruchrechnung und Polynomdivision
Lektion 4 - Wertetabellen von Funktionen
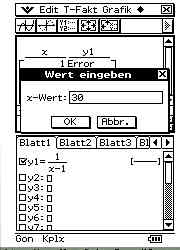
|
Arbeitsaufgaben:
- [Drucke Dir das Arbeitsblatt aus] und lies es Dir aufmerksam durch.
- Übungsaufgaben:
|
Lektion 5 - Grenzwerte für x -> unendlich und an Definitionslücken
Arbeitsaufgaben:
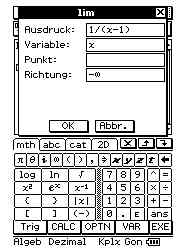 Grenzwert für x-> minus undendlich /für plus uendlich kein Vorzeichen Grenzwert für x-> minus undendlich /für plus uendlich kein Vorzeichen
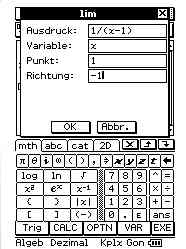 Grenzwert links (-1) Grenzwert rechts +1 z.B. an einer Polstelle (Stelle (Punkt) 1) Grenzwert links (-1) Grenzwert rechts +1 z.B. an einer Polstelle (Stelle (Punkt) 1)
Zusammenfassende Übung - Kurvendiskussion ganz- und gebrochenrationaler Funktionen mit Mitteln der 10. Klasse
|
Arbeitsaufgaben:
- [ Drucke Dir das Arbeitsblatt aus] und lies es Dir aufmerksam durch.
- Die folgenden Funktionen sollen jeweils mit den herkömmlichen Methoden und mittels des ClassPads 330 Nullstellen, Polstellen, stetig hebbare Definitionslücken und Grenzwert gegen Unendlich untersucht werden. Darüberhinaus soll eine Wertetabelle in einem geeigneten Bereich und eine Skizze des Funktionsgraphen angefertigt werden. Bildet dazu vier Gruppen, von denen zwei klassisch und zwei mit Verwendung des ClassPad 330 vorgehen.
|
Lektion 7: Gleichungssysteme lösen
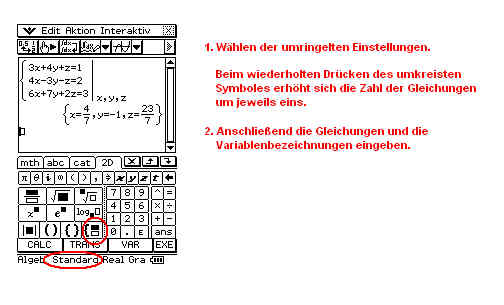
Lektion 8: Trigonometrische Probleme lösen
Lektion 9: Ableitungsfunktion bestimmen
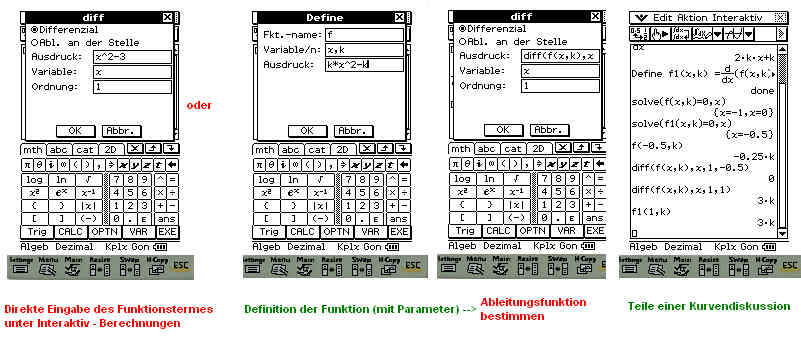
Lektion 10: Bestimmte und unbestimmte Integrale berechnen
|

Lektion 11: Arbeiten mit Vektoren
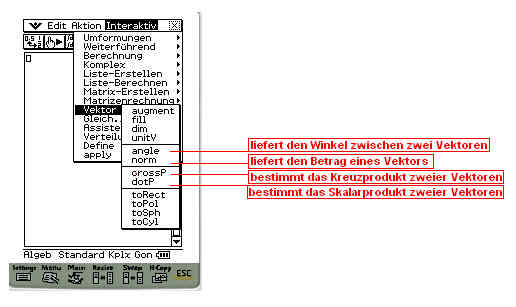
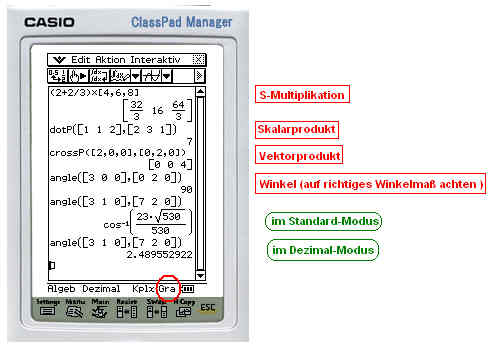
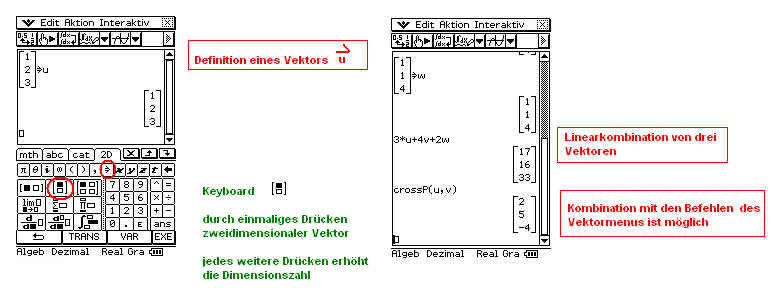
|

Homepage des Aktionstages
|
|