M8 Term und Graph bei gebrochen-rationalen Funktionen: Unterschied zwischen den Versionen

Aus RSG-Wiki
Wechseln zu: Navigation, Suche
Zeile 1: Zeile 1:
−
_NOCACHE_
+
__NOCACHE__
 
Auf dieser Seite soll der Zusammenhang zwischen dem Graphen und dem Funktionsterm einer gebrochen-rationalen Funktion näher untersucht werden. Dabei geht es um zwei Fragestellungen:<br>
 
Auf dieser Seite soll der Zusammenhang zwischen dem Graphen und dem Funktionsterm einer gebrochen-rationalen Funktion näher untersucht werden. Dabei geht es um zwei Fragestellungen:<br>
 
1. Wie finde ich aus einem gegebenen Graphen den passenden Funktionsterm.<br>
 
1. Wie finde ich aus einem gegebenen Graphen den passenden Funktionsterm.<br>

Version vom 18. Juni 2020, 08:08 Uhr

Auf dieser Seite soll der Zusammenhang zwischen dem Graphen und dem Funktionsterm einer gebrochen-rationalen Funktion näher untersucht werden. Dabei geht es um zwei Fragestellungen:
1. Wie finde ich aus einem gegebenen Graphen den passenden Funktionsterm.
2. Wie kann man "leicht" aus einem gegebenen Funktionsterm den Graphen angeben.

Zur Beantwortung sind die folgenden Eigenschaften gebrochen-rationaler Funktionen hilfreich.
Ausgangspunkt unserer Betrachtungen ist die indirekte Proportionalität 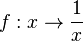f: x \rightarrow \frac{1}{x} . Die Funktion ist für 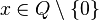x \in Q\setminus \left \{ 0 \right \} definiert. Die Funktionsgleichung ist 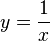y = \frac{1}{x} und der Funktionsgraph

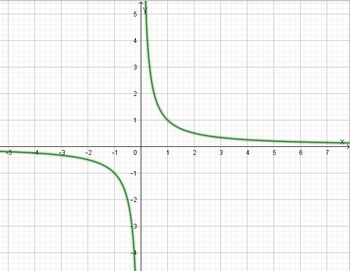
1-x-.jpg


Inhaltsverzeichnis

Definitionslücke - senkrechte Asymptote

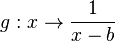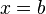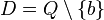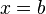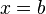Die Funktion g: x \rightarrow \frac{1}{x-b} ist für x = b nicht definiert, da wenn man b für x einsetzt im Nenner Null steht. Das ist nicht zulässig. Also ist D=Q\setminus \left \{ b \right \}. An der Stelle x = b hat die Funktion g eine Definitionslücke. Der Graph eine senkrechte Asymptote. x = b ist eine Polstelle des Graphen.


30px   Aufgabe 1

Im folgenden Applet ist der Graph der indirekten Proportionalität f mit f(x) = \frac{1}{x} ( grün) und der Graph der Funktion g mit g(x) = \frac{1}{1-b} ( rot) eingezeichnet. Desweiteren ist die senkrechte Asymptote x = b ( blau) eingezeichnet. Mit dem Schieberegler kannst du den Wert von b ändern.


Der Schieberegler ist auf b = 0 eingestellt. 1. Gib die Funktionsgleichung von g und die Gleichung der Asymptote an.

2. Stelle nun den Schieberegler auf b = 1.
Was passiert mit dem Graphen von g und mit der Asymptote?
Gib die Funktionsgleichung von g und die Gleichung der Asymptote an.

Stelle nun den Schieberegler wieder auf b = 0. Die Graphen von f und g liegen nun wieder aufeinander.
3. Stelle nun den Schieberegler auf b = -2.
Was passiert mit dem Graphen von g und mit der Asymptote?
Gib die Funktionsgleichung von g und die Gleichung der Asymptote an.

1. Die Funktionsgleichung ist 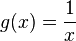g(x) = \frac{1}{x} und die Gleichung der Asymptote x = 0 .

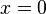2. Der Graph von f der indirekten Proportionalität wird um b=1 in positive x-Richtung verschoben.
Ebenso wird die Asymptote um 1 in positive x-Richtung verschoben.
Die Funktionsgleichung ist 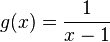g(x) = \frac{1}{x-1} und die Gleichung der Asymptote x = 1 .

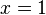3. Der Graph von f der indirekten Proportionalität wird um 2 in negative x-Richtung verschoben.
Ebenso wird die Asymptote um 2 in negative x-Richtung verschoben.

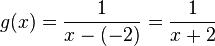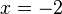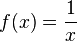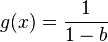Die Funktionsgleichung ist g(x) = \frac{1}{x-(-2)}=\frac{1}{x+2} und die Gleichung der Asymptote x = -2 .

Vorzeichenwechsel

Spiegelung an der x-Achse

Streckung und Stauchung

waagrechte Asymptote

Von „http://rsg.zum.de/index.php?title=M8_Term_und_Graph_bei_gebrochen-rationalen_Funktionen&oldid=10340“