M11 Vektoren: Unterschied zwischen den Versionen
| Zeile 16: | Zeile 16: | ||
* der Anfangspunkt des Repräsentanten des Vektors der Ursprung ist und die Spitze (Endpunkt) der Punkt B(b<sub>1</sub>;b<sub>2</sub>;b<sub>3</sub>) durch <math>\vec v = \left ( \begin{array}{c} b_1 \\\ b_2 \\\ b_3 \end{array}\right) </math> oder <br> | * der Anfangspunkt des Repräsentanten des Vektors der Ursprung ist und die Spitze (Endpunkt) der Punkt B(b<sub>1</sub>;b<sub>2</sub>;b<sub>3</sub>) durch <math>\vec v = \left ( \begin{array}{c} b_1 \\\ b_2 \\\ b_3 \end{array}\right) </math> oder <br> | ||
* der Anfangspunkt A(a<sub>1</sub>;a<sub>2</sub>;a<sub>3</sub>) und die Spitze (Endpunkt) B(b<sub>1</sub>;b<sub>2</sub>;b<sub>3</sub>) ist durch die Koordinatendifferenzen des Endpunkts und des Anfangspunkts, also <math>\vec v = \left ( \begin{array}{c} b_1 - a_1 \\\ b_2 - a_2 \\\ b_3 - a_3 \end{array}\right) </math> . <br> | * der Anfangspunkt A(a<sub>1</sub>;a<sub>2</sub>;a<sub>3</sub>) und die Spitze (Endpunkt) B(b<sub>1</sub>;b<sub>2</sub>;b<sub>3</sub>) ist durch die Koordinatendifferenzen des Endpunkts und des Anfangspunkts, also <math>\vec v = \left ( \begin{array}{c} b_1 - a_1 \\\ b_2 - a_2 \\\ b_3 - a_3 \end{array}\right) </math> . <br> | ||
| − | Für Vektoren verwendet man eine '''Spaltenschreibweise''' <math>\vec v = \left ( \begin{array}{c} v_1 \\\ v_2 \\\ v_3 \end{array}\right) </math> und der Vektor <math>\vec v </math> ist ein '''Spaltenvektor''' des Raumes. <math> v_1, v_2, v_3</math> heißen Koordinaten des Vektors <math>\v </math>.}} | + | Für Vektoren verwendet man eine '''Spaltenschreibweise''' <math>\vec v = \left ( \begin{array}{c} v_1 \\\ v_2 \\\ v_3 \end{array}\right) </math> und der Vektor <math>\vec v </math> ist ein '''Spaltenvektor''' des Raumes. <math> v_1, v_2, v_3</math> heißen Koordinaten des Vektors <math>\vec v </math>.}} |
Version vom 12. Dezember 2020, 16:13 Uhr
Aus der Physik kennt man Größen wie Geschwindigkeit, Impuls, Kraft, die nicht nur einen Betrag sondern auch eine Richtung haben. Die Richtung wird durch einen Pfeil angegeben. Je Größer die Geschwindigkeit, der Impuls, die Kraft ist desto länger ist der Pfeil.
In der Mathematik kennt man Pfeile oder Vektoren von einer Verschiebung. In diesem Video
wird erkärt wie man eine Verschiebung im R2 mit Hilfe eines Vektors beschreibt.
 Merke:
Ein Vektor ist die Menge aller gleichlangen, parallelen und gleichgerichteten Pfeile. Jeder Pfeil ist ein Repräsentant des Vektors. Jeder Repräsentant legt den Vektor fest. In einem Koordinatensystem legt man einen Vektor
Für Vektoren verwendet man eine Spaltenschreibweise |
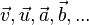bezeichnet.
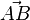und verwendet dies auch für den Vektor , also 
.
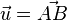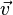durch Koordinaten fest. Dies erfolgt, wenn 
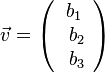oder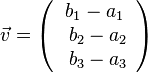 
. 
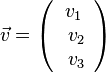und der Vektor 
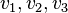heißen Koordinaten des Vektors 
