Das Fadenpendel: Unterschied zwischen den Versionen
| (19 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
Beim mathematischen Pendel handelt es sich um ein idealisiertes Pendel, ein "punktförmiger" Pendelkörper hängt an einem masselosen Seil oder Stange.<br> | Beim mathematischen Pendel handelt es sich um ein idealisiertes Pendel, ein "punktförmiger" Pendelkörper hängt an einem masselosen Seil oder Stange.<br> | ||
| − | {{Aufgaben-blau||2=1. Beschreibe die Energien, die beim Fadenpendel auftreten. <br> | + | {{Aufgaben-blau|1|2=1. Beschreibe die Energien, die beim Fadenpendel auftreten. <br> |
2. Ein 1m langes Fadenpendel (Masse des Pendelkörpers m = 100g) wird um 20° ausgelenkt. Auf welche Höhe h über der Ruhelage ist das Pendel? Wie groß ist seine Lageenergie gegenüber der Ruhelage? <br> | 2. Ein 1m langes Fadenpendel (Masse des Pendelkörpers m = 100g) wird um 20° ausgelenkt. Auf welche Höhe h über der Ruhelage ist das Pendel? Wie groß ist seine Lageenergie gegenüber der Ruhelage? <br> | ||
c)Das Pendel wird losgelassen. Mit welcher Geschwindigkeit bewegt es sich durch die Ruhelage?}} | c)Das Pendel wird losgelassen. Mit welcher Geschwindigkeit bewegt es sich durch die Ruhelage?}} | ||
{{Lösung versteckt|1=Ist das Pendel ausgelenkt, so hat es Lageenergie. Lässt man es los, dann wird die Lageenergie in Bewegungsenergie umgewandelt. Passiert der Pendelkörper die Ruhelage, dann hat man keine Lageenergie und die Bewegungsenergie ist maximal. Bei der weiteren Bewegung wird nun die Bewegungsenergie wieder in Lageenergie umgewandelt. Im Umkehrpunkt hat der Körper wieder maximale Lageenergie und keine Bewegungsenergie.<br> | {{Lösung versteckt|1=Ist das Pendel ausgelenkt, so hat es Lageenergie. Lässt man es los, dann wird die Lageenergie in Bewegungsenergie umgewandelt. Passiert der Pendelkörper die Ruhelage, dann hat man keine Lageenergie und die Bewegungsenergie ist maximal. Bei der weiteren Bewegung wird nun die Bewegungsenergie wieder in Lageenergie umgewandelt. Im Umkehrpunkt hat der Körper wieder maximale Lageenergie und keine Bewegungsenergie.<br> | ||
| − | b) h = 1m - 1m·cos( | + | b) h = 1m - 1m·cos(20°) = 0,06m = 6cm. E<sub>L</sub> = mgh = 0,1kg·9,8N/kg·0,06m=0,0588J<br> |
Falls du nicht weißt wie du auf h kommst, in [https://www.youtube.com/watch?v=K6e4fVPFLE8 diesem Film] wird es erklärt.<br> | Falls du nicht weißt wie du auf h kommst, in [https://www.youtube.com/watch?v=K6e4fVPFLE8 diesem Film] wird es erklärt.<br> | ||
c) Nach dem Energieerhaltungssatz ist E<sub>B</sub> = E<sub>L</sub> = 0,0588J, also <math>E_B = \frac{1}{2}mv^2</math> und <math>v = \sqrt{\frac{2E_B}{m}} = \sqrt{\frac{2\cdot0,0588J}{0,1kg}}=1,084\frac{m}{s^2}</math> .}} | c) Nach dem Energieerhaltungssatz ist E<sub>B</sub> = E<sub>L</sub> = 0,0588J, also <math>E_B = \frac{1}{2}mv^2</math> und <math>v = \sqrt{\frac{2E_B}{m}} = \sqrt{\frac{2\cdot0,0588J}{0,1kg}}=1,084\frac{m}{s^2}</math> .}} | ||
| − | {{Aufgaben-blau||2=Welche Kräfte wirken auf einen ausgelenkten Pendelkörper?}} | + | {{Aufgaben-blau|2|2=Welche Kräfte wirken auf einen ausgelenkten Pendelkörper?}} |
{{Lösung versteckt|Auf einen ausgelenkten Pendelkörper wirken die Gewichtskraft, die Haltekraft des Seils und die Tangentialkraft. Die Tangentialkraft ist die rücktreibende Kraft, die das Pendel wieder in die Ruhelage bringen will. <br> | {{Lösung versteckt|Auf einen ausgelenkten Pendelkörper wirken die Gewichtskraft, die Haltekraft des Seils und die Tangentialkraft. Die Tangentialkraft ist die rücktreibende Kraft, die das Pendel wieder in die Ruhelage bringen will. <br> | ||
[[File:Fadenpendel_1.jpg|200px]]}} | [[File:Fadenpendel_1.jpg|200px]]}} | ||
| − | {{Aufgaben-blau||2=Schaue dir diesen Film an {{#ev:youtube |f_WUOH3tF78|350}} <br> | + | {{Aufgaben-blau|3|2=Schaue dir diesen Film an {{#ev:youtube |f_WUOH3tF78|350}} <br> |
1. Was ist beim Fadenpendel die Schwingungsdauer T?<br> | 1. Was ist beim Fadenpendel die Schwingungsdauer T?<br> | ||
| − | 2. Welche Faktoren können die Schwingungsdauer <br> | + | 2. Welche Faktoren können die Schwingungsdauer beeinflussen?<br> |
3. Wie wurde in dem Video gemessen und was war das Ergebnis?<br> | 3. Wie wurde in dem Video gemessen und was war das Ergebnis?<br> | ||
4. Wie lautet die Formel für die Schwingungsdauer T eines Fadenpendels der Länge l für Auslenkwinkel < 10°?<br> | 4. Wie lautet die Formel für die Schwingungsdauer T eines Fadenpendels der Länge l für Auslenkwinkel < 10°?<br> | ||
| Zeile 28: | Zeile 28: | ||
{{Lösung versteckt|1=1. Die Schwingungsdauer T ist die Zeit die vergeht, wenn der Pendelkörper losgelassen wird bis er wieder an dieser Stelle ist.<br> | {{Lösung versteckt|1=1. Die Schwingungsdauer T ist die Zeit die vergeht, wenn der Pendelkörper losgelassen wird bis er wieder an dieser Stelle ist.<br> | ||
| − | 2. Länge des Pendels, Masse des Pendelkörpers, Auslenkwinkel<br> | + | 2. Man kann annehmen, dass die Länge des Pendels, die Masse des Pendelkörpers, die Auslenkwinkel die Schwingungsdauer beeinflussen.<br> |
3. a) Verschiedene Auslenkwinkel, Masse und Länge bleiben gleich. Die Schwingungsdauer ist immer gleich.<br> | 3. a) Verschiedene Auslenkwinkel, Masse und Länge bleiben gleich. Die Schwingungsdauer ist immer gleich.<br> | ||
b) Verschiedene Masse, Pendellänge und Auslenkwinkel bleiben gleich. Die Schwingungsdauer ist immer gleich.<br> | b) Verschiedene Masse, Pendellänge und Auslenkwinkel bleiben gleich. Die Schwingungsdauer ist immer gleich.<br> | ||
| Zeile 36: | Zeile 36: | ||
{{Merksatz|MERK=Je kürzer das Pendel desto kürzer ist die Schwingungsdauer<br> | {{Merksatz|MERK=Je kürzer das Pendel desto kürzer ist die Schwingungsdauer<br> | ||
Dei Schwingungsdauer T eines Fadenpendels der Länge l ist <center><math>T = 2 \pi \sqrt{\frac{l}{g}}</math></center><br> | Dei Schwingungsdauer T eines Fadenpendels der Länge l ist <center><math>T = 2 \pi \sqrt{\frac{l}{g}}</math></center><br> | ||
| − | Die Schwingungsdauer ist von der Masse des Pendelkörpers unabhängig, ebenso für Auslenkwinkel < | + | Die Schwingungsdauer ist von der Masse des Pendelkörpers unabhängig, ebenso für Auslenkwinkel < 10°.}} |
| + | |||
| + | In diesem Video sieht man, dass die Schwingungsdauer eines Fadenpendels nicht von der Masse des Pendelkörpers abhängt, sowie die Abhängigkeit von der Pendellänge. | ||
| + | <center>{{#ev:youtube |2N9cKCcza3U|350}}</center> | ||
| Zeile 42: | Zeile 45: | ||
<center>[[File:Fadenpendel_1.jpg|200px]]</center><br> | <center>[[File:Fadenpendel_1.jpg|200px]]</center><br> | ||
Die Kraft F ist Kathete im Kräftedreieck und es ist <math>F = G\cdot sin(\varphi) </math> .<br> | Die Kraft F ist Kathete im Kräftedreieck und es ist <math>F = G\cdot sin(\varphi) </math> .<br> | ||
| − | Für kleine Winkel <math>\varphi </math> gilt <math> sin \varphi \approx \ | + | Für kleine Winkel <math>\varphi </math> gilt <math> sin \varphi \approx \varphi</math>. |
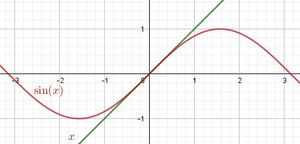
| − | {{aufgaben-blau||2=In diesem Diagramm sind die Graphen der Sinusfunktion f :x → sin(x) und der Idendität g: x → x dargestellt. <br> | + | {{aufgaben-blau|4|2=In diesem Diagramm sind die Graphen der Sinusfunktion f :x → sin(x) und der Idendität g: x → x dargestellt. <br> |
[[Datei:Kleinwinkelnäherung 1.jpg|300px]]<br> | [[Datei:Kleinwinkelnäherung 1.jpg|300px]]<br> | ||
Was stellst du in der Nähe des Ursprungs fest? Was kannst du über die zwei Graphen bzw. deren Funktionen dort aussagen?}} | Was stellst du in der Nähe des Ursprungs fest? Was kannst du über die zwei Graphen bzw. deren Funktionen dort aussagen?}} | ||
| Zeile 50: | Zeile 53: | ||
{{Lösung versteckt|1=In der Nähe des Ursprungs verlaufen die zwei Graphen übereinanderliegend. Die beiden Graphen fallen dort zusammen. Die Funktionswerte von sin(x) und x sind gleich.}} | {{Lösung versteckt|1=In der Nähe des Ursprungs verlaufen die zwei Graphen übereinanderliegend. Die beiden Graphen fallen dort zusammen. Die Funktionswerte von sin(x) und x sind gleich.}} | ||
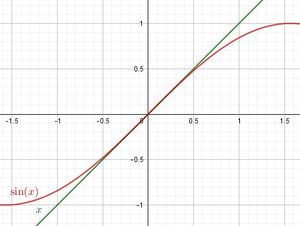
| − | {{aufgaben-blau||2=Um die letzte Aussage näher zu untersuchen ist in der Nähe des Ursprung das Diagramm vergrößert. <br> | + | {{aufgaben-blau|5|2=Um die letzte Aussage näher zu untersuchen ist in der Nähe des Ursprung das Diagramm vergrößert. <br> |
[[Datei:Kleinwinkelnäherung 2.jpg|300px]]<br> | [[Datei:Kleinwinkelnäherung 2.jpg|300px]]<br> | ||
a) Lies aus dem Diagramm ab für welche x gilt: sin(x) = x (Die beiden Graphen liegen aufeinander.)<br> | a) Lies aus dem Diagramm ab für welche x gilt: sin(x) = x (Die beiden Graphen liegen aufeinander.)<br> | ||
| Zeile 65: | Zeile 68: | ||
Für x < 0,2 gilt sin(x) ≈ x bzw. für Winkel <math>\varphi \leq 10^o</math> gilt <math> sin(\varphi) \approx \varphi</math> .}} | Für x < 0,2 gilt sin(x) ≈ x bzw. für Winkel <math>\varphi \leq 10^o</math> gilt <math> sin(\varphi) \approx \varphi</math> .}} | ||
| − | {{Aufgaben-blau||2=Welche Beziehung besteht in dieser Zeichnung <br> | + | {{Aufgaben-blau|6|2=Welche Beziehung besteht in dieser Zeichnung <br> |
[[File:Fadenpendel_1.jpg|200px]]<br> | [[File:Fadenpendel_1.jpg|200px]]<br> | ||
zwischen x, l und <math>\varphi</math> ?}} | zwischen x, l und <math>\varphi</math> ?}} | ||
| Zeile 83: | Zeile 86: | ||
Die rücktreibende Kraft F ist also direkt proportional zur Auslenkung x. }} | Die rücktreibende Kraft F ist also direkt proportional zur Auslenkung x. }} | ||
| − | Man hat also beim Fadenpendel ein Kraftgesetz, das wie beim Federpendel besagt, dass die rücktreibende Kraft direkt proportional zur Auslenkung ist mit <math>F=-\cdot \frac{G}{l}\cdot x</math> . | + | Man hat also beim Fadenpendel ein Kraftgesetz, das wie beim Federpendel besagt, dass die rücktreibende Kraft direkt proportional zur Auslenkung ist mit <math>F=-\cdot \frac{G}{l}\cdot x</math> . Schaue dir als Zusammenfassung dieses Video an:<br> |
| + | {{#ev:youtube |sy7G8Jmwmhc|350}} . | ||
| − | {{Aufgaben-blau||2=Vergleiche das die rücktreibende Kraft des Federpendels mit der rücktreibenden Kraft der Fadenpendels.}} | + | {{Aufgaben-blau|7|2=Vergleiche das die rücktreibende Kraft des Federpendels mit der rücktreibenden Kraft der Fadenpendels.}} |
{{Lösung versteckt|1=Federpendel F = - D·s <br> | {{Lösung versteckt|1=Federpendel F = - D·s <br> | ||
| Zeile 101: | Zeile 105: | ||
{{Merksatz|MERK=Für die Schwingungsdauer einer Fadenpendels bei kleinen Auslenkungen gilt<br> | {{Merksatz|MERK=Für die Schwingungsdauer einer Fadenpendels bei kleinen Auslenkungen gilt<br> | ||
| − | <center> | + | <center><math> T = 2\pi\sqrt{\frac{l}{g}}</math> .</center>}} |
| + | |||
| + | {{Versuch|1=Überprüfe die Gleichung <math>T = 2\pi\sqrt{\frac{l}{g}}</math> auf der [https://www.walter-fendt.de/html5/phde/pendulum_de.htm Seite], indem du die Werte von l, m, A, f (immer nur einen Wert variieren!) veränderst und T im Diagramm abliest.<br> | ||
| + | Verdoppele bzw. halbiere die Pendellänge l.<br> | ||
| + | Verdoppele bzw. halbiere die Masse m des Pendelkörpers.<br> | ||
| + | Verdoppele bzw. halbiere die Auslenkung<br> | ||
| + | Verdoppele bzw. halbiere die Fallbeschleunigung g. <br> | ||
| + | Was passiert mit den einzelnen Größen, wenn man die Amplitude verdoppelt bzw. halbiert. }} | ||
| + | |||
| + | {{Aufgaben-blau|8|2=Ein Sekundenpendel ist ein Pendel, das für eine Halbschwingung genau eine Sekunde benötigt.<br> | ||
| + | a) Wie groß ist die Schwingungsdauer T eines Sekundenpendels?<br> | ||
| + | b) Bestimme die Länge l des Sekundenpendels.<br> | ||
| + | c) Welche Schwingungsdauer hat ein Pendel der Länge l = 1m?<br> | ||
| + | Nach wie vielen Schwingungen geht das Pendel 1min gegenüber dem Sekundenpendel nach? <br> | ||
| + | Wie lange schwingt das Pendel dabei? }} | ||
| + | |||
| + | {{Lösung versteckt|1=a) Eine Halbschwingung dauert 1s, also ist T = 2s.<br> | ||
| + | b) <math>T = 2\pi\sqrt{\frac{l}{g}}</math> formt man um <math>l = \frac{g\cdot T^2}{4\pi^2}</math> . Damit ist | ||
| + | <math>l = \frac{9,8 \frac{m}{s^2} \cdot (2s)^2}{4 \cdot \pi^2} = 0,993m </math><br> | ||
| + | c) <math>T = 2\pi\sqrt{\frac{1m}{9,8\frac{m}{s^2}}} = 2,007s</math><br> | ||
| + | n·0,007s = 60s, n = 8571,43<br> | ||
| + | Nach 8571,43 Schwingungen ist die Zeit t = 17142,86s = 4h 45min 32s vergangen.}} | ||
| + | |||
| + | {{Aufgaben-blau|9|2=Bearbeite das [https://www.leifiphysik.de/mechanik/mechanische-schwingungen/aufgabe/quiz-zur-schwingungsdauer-eines-fadenpendels Quiz zur Schwingunsdauer eines Fadenpendels] und das [https://www.leifiphysik.de/mechanik/mechanische-schwingungen/aufgabe/quiz-zum-fadenpendel Quiz zum Fadenpendel] }} | ||
| + | |||
| + | {{Aufgaben-blau|10|2=Bearbeite die Aufgaben bei Leifiphysik:<br> | ||
| + | a) [https://www.leifiphysik.de/mechanik/mechanische-schwingungen/aufgabe/kinderschaukel Kinderschaukel]<br> | ||
| + | b) [https://www.leifiphysik.de/mechanik/mechanische-schwingungen/aufgabe/sekundenpendel Sekundenpendel]<br> | ||
| + | c) [https://www.leifiphysik.de/mechanik/mechanische-schwingungen/aufgabe/hoehenbestimmung-mittels-pendel Höhenbestimmung] }} | ||
| + | |||
| + | {{Versuch|1=Wenn ihr zuhause eine Pendeluhr habt, dann messt doch mal die Pendellänge l und die Schwingungsdauer T der Uhr und überprüft die Formel.}} | ||
| + | |||
| + | {{Versuch|1= [https://www.youtube.com/watch?v=q3_m1JW1ttQ&t=1s Ein Smartphone-Experiment] }} | ||
| − | {{ | + | {{Versuch|1=Schaue dir die zwei Videos zum Foucault-Pendel an. <br> |
| + | {{#ev:youtube |7-q015Qdza8|350}} {{#ev:youtube |tB5ql-ZmhLw|350}} }} | ||
Aktuelle Version vom 2. Februar 2021, 11:51 Uhr
Im Gegensatz zum Federpendel (meist hat man ja keine Feder zuhause) kannst du ein Fadenpendel leicht daheim selbst anfertigen.
Ein Fadenpendel besteht aus einem Körper, der an einem befestigten Faden aufgehängt ist. Der Pendelkörper wird um ein kleines Stück aus der Ruhelage ausgelenkt und dort losgelassen.
Beim mathematischen Pendel handelt es sich um ein idealisiertes Pendel, ein "punktförmiger" Pendelkörper hängt an einem masselosen Seil oder Stange.
Ist das Pendel ausgelenkt, so hat es Lageenergie. Lässt man es los, dann wird die Lageenergie in Bewegungsenergie umgewandelt. Passiert der Pendelkörper die Ruhelage, dann hat man keine Lageenergie und die Bewegungsenergie ist maximal. Bei der weiteren Bewegung wird nun die Bewegungsenergie wieder in Lageenergie umgewandelt. Im Umkehrpunkt hat der Körper wieder maximale Lageenergie und keine Bewegungsenergie.
b) h = 1m - 1m·cos(20°) = 0,06m = 6cm. EL = mgh = 0,1kg·9,8N/kg·0,06m=0,0588J
Falls du nicht weißt wie du auf h kommst, in diesem Film wird es erklärt.
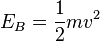 und
und 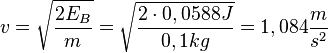 .
.
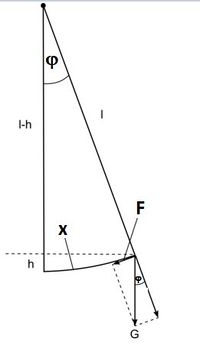
Auf einen ausgelenkten Pendelkörper wirken die Gewichtskraft, die Haltekraft des Seils und die Tangentialkraft. Die Tangentialkraft ist die rücktreibende Kraft, die das Pendel wieder in die Ruhelage bringen will.
1. Die Schwingungsdauer T ist die Zeit die vergeht, wenn der Pendelkörper losgelassen wird bis er wieder an dieser Stelle ist.
2. Man kann annehmen, dass die Länge des Pendels, die Masse des Pendelkörpers, die Auslenkwinkel die Schwingungsdauer beeinflussen.
3. a) Verschiedene Auslenkwinkel, Masse und Länge bleiben gleich. Die Schwingungsdauer ist immer gleich.
b) Verschiedene Masse, Pendellänge und Auslenkwinkel bleiben gleich. Die Schwingungsdauer ist immer gleich.
c) Verschiedene Pendellängen, Masse und Auslenkwinkel bleiben gleich. Bei Veränderung der Länge l verändert sich auch die Schwingungsdauer. Je Länger das Pendel ist, desto größer ist die Schwingungsdauer.
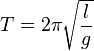
|
Merke:
Je kürzer das Pendel desto kürzer ist die Schwingungsdauer 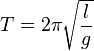 Die Schwingungsdauer ist von der Masse des Pendelkörpers unabhängig, ebenso für Auslenkwinkel < 10°. |
In diesem Video sieht man, dass die Schwingungsdauer eines Fadenpendels nicht von der Masse des Pendelkörpers abhängt, sowie die Abhängigkeit von der Pendellänge.
Um dieses qualitative Ergebnis zu verifizieren, analysieren wir die Bewegung. Dazu legen wir ein Koordinatensystem in die Ruheposition.

Die Kraft F ist Kathete im Kräftedreieck und es ist 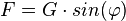 .
.
Für kleine Winkel  gilt
gilt 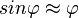 .
.
a) Es ist sin(x) = x für -0,2 ≤ x ≤ x.
b) x = 0,2 wird mittels 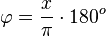 , also
, also 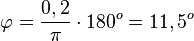 .
.
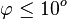 gilt
gilt 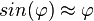
|
Merke:
Kleinwinkelnäherung Für x < 0,2 gilt sin(x) ≈ x bzw. für Winkel |
 berechnen zu
berechnen zu  gilt
gilt 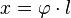 .
.
Also ist 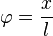 .
.
Für die rücktreibende Kraft F hatten wir aus dem Kräftedreieck 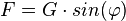 . Ersetzt man
. Ersetzt man  durch
durch 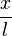 , dann erhält man
, dann erhält man 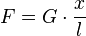 .
.
Nun müssen wir noch die Richtungen berücksichtigen.
Wird das Pendel nach rechts (x>0) ausgelenkt, dann wirkt die Kraft FH nach links, wird der Körper nach links ausgelenkt (x<0), wirkt die Kraft FH nach rechts. In beiden Fällen ist die Kraft entgegengesetzt zu x gerichtet, sie wirkt also entgegen der Orientierung des Koordinatensystems.
|
Merke:
Für die rücktreibende Kraft F beim Fadenpendel gilt bei Auslenkungen ≤ 10° 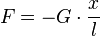 Die rücktreibende Kraft F ist also direkt proportional zur Auslenkung x. |
Man hat also beim Fadenpendel ein Kraftgesetz, das wie beim Federpendel besagt, dass die rücktreibende Kraft direkt proportional zur Auslenkung ist mit 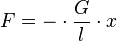 . Schaue dir als Zusammenfassung dieses Video an:
. Schaue dir als Zusammenfassung dieses Video an:
Federpendel F = - D·s
Fadenpendel 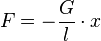
Beide rücktreibende Kräfte sind entgegensetzt zur Auslenkung, daher das Minuszeichen, welches die Richtung im Koordinantensystem angeibt
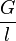 beim Fadenpendel.
beim Fadenpendel.Löst man F = m·a nach a auf, so erhält man für die Beschleunigung a beim Fadenpendel 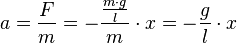 .
.
Beim Federpendel hatten wir auch eine Gleichung für die Beschleunigung = - Konstante mal Auslenkung. Eine solche Schwingung ist eine harmonische Schwingung.
|
Merke:
Das Fadenpendel macht für kleine Auslenkungen eine harmonische Schwingung. |
Durch Vergleich bei den Schwingungen hatte man 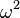 = Konstante der bei der Beschleunigung. Das bedeutet hier
= Konstante der bei der Beschleunigung. Das bedeutet hier
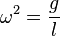 . Für die Schwingungsdauer T erhält man wegen
. Für die Schwingungsdauer T erhält man wegen 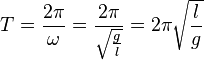 . Das ist die Formel, die im Video aufgestellt wurde.
. Das ist die Formel, die im Video aufgestellt wurde.
|
Merke:
Für die Schwingungsdauer einer Fadenpendels bei kleinen Auslenkungen gilt 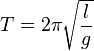 . . |
30px Versuch
Überprüfe die Gleichung |
a) Eine Halbschwingung dauert 1s, also ist T = 2s.
b) 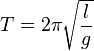 formt man um
formt man um 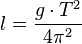 . Damit ist
. Damit ist
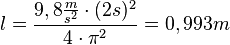
c) 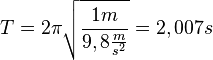
n·0,007s = 60s, n = 8571,43
30px Versuch
Wenn ihr zuhause eine Pendeluhr habt, dann messt doch mal die Pendellänge l und die Schwingungsdauer T der Uhr und überprüft die Formel. |
30px Versuch
|
30px Versuch
Schaue dir die zwei Videos zum Foucault-Pendel an. |