M11 Vektorprodukt: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „__NOCACHE__ Bisher haben wir zwei Multiplikationen bei Vektoren kennengelernt. * die S-Multiplikation, die Multiplikation einer Zahl mit einem Vektor * das S…“) |
|||
| (18 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
* die S-Multiplikation, die Multiplikation einer Zahl mit einem Vektor | * die S-Multiplikation, die Multiplikation einer Zahl mit einem Vektor | ||
* das Skalarprodukt, die Multiplikation zweier Vektoren, dessen Ergebnis eine Zahl ist. | * das Skalarprodukt, die Multiplikation zweier Vektoren, dessen Ergebnis eine Zahl ist. | ||
| − | |||
{| class="wikitable" | {| class="wikitable" | ||
| Zeile 17: | Zeile 16: | ||
b) <math>\vec n = \left ( \begin{array}{c} 1 \\\ 0 \\\ 0 \end{array}\right)</math><br> | b) <math>\vec n = \left ( \begin{array}{c} 1 \\\ 0 \\\ 0 \end{array}\right)</math><br> | ||
c) <math>\vec n = \left ( \begin{array}{c} 0 \\\ 1 \\\ 0 \end{array}\right)</math><br> | c) <math>\vec n = \left ( \begin{array}{c} 0 \\\ 1 \\\ 0 \end{array}\right)</math><br> | ||
| − | d) Es ist <math>\vec a \circ \vec b = 0</math>, also stehen <math>\vec a</math> und <math> \vec b</math> senkrecht zueinander. Dann findet man auch einen dritten Vektor, der jeweils senkrecht zu ihnen steht, z.B. <math>\vec n=\left ( \begin{array}{c} 1 \\\ 0 \\\ -1 \end{array}\right) | + | d) Es ist <math>\vec a \circ \vec b = 0</math>, also stehen <math>\vec a</math> und <math> \vec b</math> senkrecht zueinander. Dann findet man auch einen dritten Vektor, der jeweils senkrecht zu ihnen steht, z.B. <math>\vec n=\left ( \begin{array}{c} 1 \\\ 0 \\\ -1 \end{array}\right)</math>. }} |
{{Merksatz|MERK=Zu den Vektoren <math>\vec a=\left ( \begin{array}{c} a_1 \\\ a_2 \\\ a_3 \end{array}\right)</math> und <math>\vec b=\left ( \begin{array}{c} b_1 \\\ b_2 \\\ b_3 \end{array}\right)</math> bildet man das '''Vektorprodukt''' <math> \vec a \times \vec b</math> durch <math> \vec a \times \vec b = \left ( \begin{array}{c} a_2b_3-a_3b_2 \\\ a_3b_1-a_1b_3 \\\ a_1b_2-a_2b_1 \end{array}\right)</math>. | {{Merksatz|MERK=Zu den Vektoren <math>\vec a=\left ( \begin{array}{c} a_1 \\\ a_2 \\\ a_3 \end{array}\right)</math> und <math>\vec b=\left ( \begin{array}{c} b_1 \\\ b_2 \\\ b_3 \end{array}\right)</math> bildet man das '''Vektorprodukt''' <math> \vec a \times \vec b</math> durch <math> \vec a \times \vec b = \left ( \begin{array}{c} a_2b_3-a_3b_2 \\\ a_3b_1-a_1b_3 \\\ a_1b_2-a_2b_1 \end{array}\right)</math>. | ||
| − | Man spricht <math> \vec a \times \vec b</math> "Vektor a Kreuz Vektor b". | + | Man spricht für <math> \vec a \times \vec b</math> : "Vektor a Kreuz Vektor b". |
<center>{{#ev:youtube |63FWetdwNb8|350}} </center> | <center>{{#ev:youtube |63FWetdwNb8|350}} </center> | ||
| + | |||
| + | Das Ergebnis des Kreuzprodukts <math> \vec a \times \vec b</math> ist ein Vektor, der senkrecht auf die Vektoren <math>\vec a</math> und <math>\vec b</math> steht. | ||
| + | |||
Eigenschaften des Vektorprodukts <math> \vec a \times \vec b</math>: | Eigenschaften des Vektorprodukts <math> \vec a \times \vec b</math>: | ||
| Zeile 31: | Zeile 33: | ||
Der Betrag des Vektorprodukts ist dann gleich der Maßzahl des Flächeninhalts des von <math>\vec a</math> und <math>\vec b </math> aufgespannten Parallelogramms. | Der Betrag des Vektorprodukts ist dann gleich der Maßzahl des Flächeninhalts des von <math>\vec a</math> und <math>\vec b </math> aufgespannten Parallelogramms. | ||
[[Datei:Flächeninhalt_Parallelogramm_Kreuzprodukt.png|250px]] | [[Datei:Flächeninhalt_Parallelogramm_Kreuzprodukt.png|250px]] | ||
| + | |||
| + | Der Flächeninhalt des von den Vektoren <math> \vec a</math> und <math>\vec b</math> aufgespannten Parallelogramms ist <math>A=|\vec a \times \vec b|</math> | ||
| + | |||
| + | Die Begründungen zu den Eigenschaften lesen Sie bitte im Buch S. 116 nach. }} | ||
| + | |||
| + | '''Beispiele''':<br> | ||
| + | 1. Für <math>\vec a=\left ( \begin{array}{c} -2 \\\ 4 \\\ 3 \end{array}\right)</math> und <math>\vec b=\left ( \begin{array}{c} 1 \\\ 2 \\\ -1 \end{array}\right)</math> ist das '''Vektorprodukt''' <math> \vec a \times \vec b</math> durch <math> \vec a \times \vec b = \left ( \begin{array}{c} 4\cdot (-1)-3\cdot 2 \\\ 3\cdot 1-(-2)\cdot (-1) \\\ -2\cdot 2-4\cdot 1 \end{array}\right) = \left ( \begin{array}{c} -10 \\\ 1 \\\ -8 \end{array}\right)</math>. | ||
| + | |||
| + | 2. Für <math>\vec a=\left ( \begin{array}{c} 1 \\\ -2 \\\ 2 \end{array}\right)</math> und <math>\vec b=\left ( \begin{array}{c} -2 \\\ 1 \\\ 2 \end{array}\right)</math> ist das '''Vektorprodukt''' <math> \vec a \times \vec b</math> durch <math> \vec a \times \vec b = \left ( \begin{array}{c} -2\cdot 2- 2\cdot 1 \\\ 2\cdot (-2)-1\cdot 2 \\\ 1\cdot 1-(-2)\cdot (-2) \end{array}\right) = \left ( \begin{array}{c} -6 \\\ -6 \\\ -3 \end{array}\right)</math>. | ||
| + | |||
| + | {{Aufgaben-blau|2|2=Ermitteln Sie drei Vektoren, die auf den Vektoren <math>\vec a=\left ( \begin{array}{c} -2 \\\ 4 \\\ 3 \end{array}\right)</math> und <math>\vec b=\left ( \begin{array}{c} 2 \\\ 2 \\\ -3 \end{array}\right)</math> senkrecht stehen. }} | ||
| + | |||
| + | {{Lösung versteckt|1=Es ist <math> \vec a \times \vec b</math> durch <math> \vec a \times \vec b = \left ( \begin{array}{c} -12-6 \\\ 6-6 \\\ -4-8 \end{array}\right) = \left ( \begin{array}{c} -18 \\\ 0 \\\ -12 \end{array}\right)</math>.<br> | ||
| + | Damit stehen die Vektoren<math>\left ( \begin{array}{c} -18 \\\ 0 \\\ -12 \end{array}\right), \left ( \begin{array}{c} 3 \\\ 0 \\\ 2 \end{array}\right), \left ( \begin{array}{c} -3 \\\ 0 \\\ -2 \end{array}\right), \left ( \begin{array}{c} 90 \\\ 0 \\\ 60 \end{array}\right), \left ( \begin{array}{c} 1,5 \\\ 0 \\\ 1 \end{array}\right)</math> senkrecht auf <math>\vec a, \vec b</math> | ||
}} | }} | ||
| + | |||
| + | {{Aufgaben-blau|3|Ermitteln Sie zu <math>\vec a=\left ( \begin{array}{c} 2 \\\ -2 \\\ 1 \end{array}\right)</math>, <math>\vec b=\left ( \begin{array}{c} 10 \\\ -6 \\\ 8 \end{array}\right)</math> und <math>\vec c=\left ( \begin{array}{c} -1 \\\ 1 \\\ 1 \end{array}\right)</math><br> | ||
| + | a) <math>\vec a \times \vec b</math><br> | ||
| + | b) <math>\vec b \times \vec c</math><br> | ||
| + | c) <math>(\vec a \times \vec b)\circ \vec c</math><br> | ||
| + | d) <math>(\vec a \times \vec b) \times \vec c</math><br> | ||
| + | e) Wie groß ist der Flächeninhalt des von den Vektoren <br> | ||
| + | i) <math>\vec a</math> und <math>\vec b</math><br> | ||
| + | ii) <math>\vec b</math> und <math>\vec c</math> aufgespannten Parallelogramms. }} | ||
| + | |||
| + | {{Lösung versteckt|1=a) <math>\vec a \times \vec b=\left ( \begin{array}{c} 2 \\\ -2 \\\ 1 \end{array}\right) \times \left ( \begin{array}{c} 10 \\\ -6 \\\ 8 \end{array}\right) = \left ( \begin{array}{c} -16+6 \\\ 10-16 \\\ -12+20 \end{array}\right) = \left ( \begin{array}{c} -10 \\\ -6 \\\ 8 \end{array}\right)</math> | ||
| + | |||
| + | b) <math>\vec b \times \vec c=\left ( \begin{array}{c} 10 \\\ -6 \\\ 8 \end{array}\right) \times \left ( \begin{array}{c} -1 \\\ 1 \\\ 1 \end{array}\right)=\left ( \begin{array}{c} -6-8 \\\ -8-10 \\\ 10-6 \end{array}\right)=\left ( \begin{array}{c} -14 \\\ -18 \\\ 4 \end{array}\right)</math> | ||
| + | |||
| + | c) <math>(\vec a \times \vec b)\circ \vec c=\left ( \begin{array}{c} -10 \\\ -6 \\\ 8 \end{array}\right) \circ \left ( \begin{array}{c} -1 \\\ 1 \\\ 1 \end{array}\right) = 10-6+8=12</math> | ||
| + | |||
| + | d) <math>(\vec a \times \vec b)\times \vec c=\left ( \begin{array}{c} -10 \\\ -6 \\\ 8 \end{array}\right) \times \left ( \begin{array}{c} -1 \\\ 1 \\\ 1 \end{array}\right) = \left ( \begin{array}{c} -6-8 \\\ -8+10 \\\ -10- 6 \end{array}\right) =\left ( \begin{array}{c} -14 \\\ 2 \\\ -16 \end{array}\right) </math> | ||
| + | |||
| + | e) i) <math>A=|\vec a \times \vec b|=\left |\left ( \begin{array}{c} -10 \\\ -6 \\\ 8 \end{array}\right) \right |=10\sqrt 2</math><br> | ||
| + | ii) <math>A=|\vec b \times \vec c|= \left | \left ( \begin{array}{c} -14 \\\ -18 \\\ 4 \end{array}\right) \right| =2\sqrt {134}</math> }} | ||
| + | |||
| + | {{Merke|1=Der Flächeninhalt des von den Vektoren <math> \vec a</math> und <math>\vec b</math> aufgespannten Parallelogramms ist <math>A=|\vec a \times \vec b|</math>. | ||
| + | <center>[[Datei:Parallelogramm-dreieck.jpg]]</center> | ||
| + | Der Flächeninhalt des von den Vektoren <math> \vec a</math> und <math>\vec b</math> aufgespannten Dreiecks ist <math>A=\frac{1}{2} |\vec a \times \vec b|</math>. }} | ||
| + | |||
| + | |||
| + | {{Aufgaben-blau|4|2=Buch S. 117 / 3 <br> | ||
| + | Buch S. 117 /4 }} | ||
| + | |||
| + | {{Lösung versteckt|1=117/3<br> | ||
| + | a) Raute, <math>A=36\sqrt 3, u=24\sqrt 2</math><br> | ||
| + | b) Quadrat, A = 50, u =<math>20 \sqrt 2</math><br> | ||
| + | c) Rechteck, A = 50, u = 30<br> | ||
| + | d) gleichschenkliges Trapez, A = 16<br> | ||
| + | e) Parallelogramm, A = 29 | ||
| + | |||
| + | 117/4 a)<math>A=\frac{1}{2} |\vec {LE} \times \vec {LA}| =\frac{1}{2} \left | \left ( \begin{array}{c} 1 \\\ 1 \\\ 1 \end{array}\right) \times \left ( \begin{array}{c} 3 \\\ 2 \\\ -4 \end{array}\right) \right| =\frac{1}{2} \left | \left ( \begin{array}{c} -6 \\\ 7 \\\ 1 \end{array}\right) \right| = \frac{1}{2} \cdot \sqrt{86}</math>. | ||
| + | |||
| + | b) <math>A=\frac{1}{2} |\vec {BE} \times \vec {BN}| =\frac{1}{2} \left | \left ( \begin{array}{c} 0 \\\ 4 \\\ -4 \end{array}\right) \times \left ( \begin{array}{c} -4 \\\ 0 \\\ 4 \end{array}\right) \right| =\frac{1}{2} \left | \left ( \begin{array}{c} 16 \\\ 16 \\\ 16 \end{array}\right) \right| = \frac{1}{2} \cdot \sqrt{768}=8\sqrt 3</math>. | ||
| + | |||
| + | c) <math>A=\frac{1}{2} |\vec {UT} \times \vec {UE}| =\frac{1}{2} \left | \left ( \begin{array}{c} -1 \\\ 8 \\\ -2 \end{array}\right) \times \left ( \begin{array}{c} 1 \\\ 8 \\\ -5 \end{array}\right) \right| =\frac{1}{2} \left | \left ( \begin{array}{c} -24 \\\ -7 \\\ -16 \end{array}\right) \right| = \frac{1}{2} \cdot \sqrt{881}</math>. | ||
| + | |||
| + | d) <math>A=\frac{1}{2} |\vec {AL} \times \vec {AF}| =\frac{1}{2} \left | \left ( \begin{array}{c} 2 \\\ 5 \\\ -2 \end{array}\right) \times \left ( \begin{array}{c} 1 \\\ 6 \\\ -1 \end{array}\right) \right| =\frac{1}{2} \left | \left ( \begin{array}{c} 7 \\\ 0 \\\ 7 \end{array}\right) \right| = \frac{7}{2} \cdot \sqrt{2}</math>. }} | ||
| + | |||
| + | |||
| + | {{Merksatz|MERK=Rechengesetze für das Vektorprodukt | ||
| + | |||
| + | * <math>\vec a \times \vec b = - (\vec b \times \vec a)</math> | ||
| + | |||
| + | * <math>(r \cdot \vec a )\times \vec b = r \cdot (\vec a \times \vec b)</math> | ||
| + | |||
| + | * <math>\vec a \times (\vec b + \vec c)=\vec a \times \vec b + \vec a \times \vec c</math> Distributivgesetz | ||
| + | |||
| + | <center>{{#ev:youtube |krAEtDA7mQU|350}}</center> }} | ||
| + | |||
| + | Im Buch gibt es dazu Aufgaben s. 117/5,6. Man muss die Definitions des Kreuzprodukts verwenden und die Koordinaten so umformen, dass die Aussage richtig wird. Wer will kann sich daran versuchen. Ich korrigiere auch die Lösung. | ||
| + | |||
| + | {{Aufgaben-blau|5|2=Buch S. 118 / 7, 8, 10 }} | ||
| + | |||
| + | {{Lösung versteckt|1=118/7 Das Kreuzprodukt <math>\left ( \begin{array}{c} x_1 \\\ x_2 \\\ 1 \end{array}\right) \times \left ( \begin{array}{c} 1 \\\ 2 \\\ 1 \end{array}\right)= \left ( \begin{array}{c} x_2-2 \\\ 1-x_1 \\\ 2x_1-x_2 \end{array}\right)= | ||
| + | \left ( \begin{array}{c} -5 \\\ 3 \\\ -1 \end{array}\right)</math> liefert ein Gleichungssystem aus drei Gleichungen mit zwei Unbekannten.<br> | ||
| + | <math>I:x_2-2=-5, II: 1-x_1=3, III: 2x_1-x_2=1 </math><br> | ||
| + | I ergibt <Math>x_2=-3</math>, II ergibt <math>x_1=-2</math>, Test in III liefert <math>2(-2)-(-3)=-1</math>. | ||
| + | |||
| + | |||
| + | 118/8 a) A(12;0;0), B(12;12;0), C(0;12;0), D(0;0;0), E(12;0;12), F(12;12;12), G(0;12;12), H(0;0;12)<br> | ||
| + | b) K ist ein Punkt in der oberen Deckfläche k<sub>3</sub>=12, ebenso L wegen l<sub>3</sub>=12, und die anderen Koordinaten von K und L liegen zwischen 0 und 12.<br> | ||
| + | M liegt auf der Kante [BF] und N auf der Kante [CG].(Koordinaten betrachten!)<br> | ||
| + | P liegt nicht auf der Würfeloberfläche, da keine seiner Koordinaten 0 oder 12 ist. Q liegt nicht auf der Kugeloberfläche, da mit q<sub>2</sub>=13 der Punkt außerhalb des Würfels liegt. | ||
| + | |||
| + | <math>2\vec {KL}=2\left ( \begin{array}{c} -6 \\\ 0 \\\ 0 \end{array}\right)=\left ( \begin{array}{c} -12 \\\ 0 \\\ 0 \end{array}\right)=\vec{MN}</math>; das Viereck KLMN ist ein Trapez, die Grundseiten haben die Längen 6cm und 12cm, die Höhe <math>4\sqrt 5</math>cm. Die Innenwinkel sind bei K 114,1°, bei L 102,6°, bei M 65,9° und bei N 77,4°.<br> | ||
| + | Der Flächeninhalt des Trapezes ergibt sich mit der Trapezformel zu <math>A=36\sqrt 5 cm^2</math>, die Umfangslänge <math>u=(6+12+4\sqrt 6 + 2\sqrt {21})cm</math> | ||
| + | |||
| + | 118/10 Es ist <math>\vec {AB}=\left ( \begin{array}{c} 2 \\\ -4 \\\ 0 \end{array}\right), \vec {BC}=\left ( \begin{array}{c} 2 \\\ 0 \\\ -6 \end{array}\right), \vec {CD}=\left ( \begin{array}{c} -2 \\\ 4 \\\ 0 \end{array}\right), \vec {DA}=\left ( \begin{array}{c} -2 \\\ 0 \\\ 6 \end{array}\right)</math>, also <math>\vec {AB}=\vec {DC}</math> und <math>\vec {BC}=\vec {AD}</math>, also ist das Viereck ein Parallelogramm. <br> | ||
| + | M erhält man durch <math>\vec m = \frac{1}{2}(\vec a + \vec c)=\left ( \begin{array}{c} 5 \\\ 0 \\\ -2 \end{array}\right)</math>, also M(5;0;-2).<br> | ||
| + | Der Flächeninhalt des Parallelogramms ist <math>A= |\vec {AB} \times \vec {AD}|=\left | \left ( \begin{array}{c} 2 \\\ -4 \\\ 0 \end{array}\right) \times \left ( \begin{array}{c} 2 \\\ 0 \\\ -6 \end{array}\right ) \right |=\left | \left ( \begin{array}{c} 24 \\\ 12 \\\ 8 \end{array}\right) \right |=28</math>. <br> | ||
| + | Wegen der Volumenformel der Pyramide <math>V=\frac{1}{3}Gh</math> ist die Höhe der Pyramide h = 9. <br> | ||
| + | Katarinas Ansatz ist der, dass man vom Mittelpunkt M neun Einheiten in Richtung des Einheitsvektors <math>\frac{1}{28}\left ( \begin{array}{c} 24 \\\ 12 \\\ 8 \end{array}\right) </math> geht. Da man von M aus in zwei entgegengesetzte Richtungen gehen kann, schreibt sie +/- . }} | ||
| + | |||
| + | <center>{{#ev:youtube |YpbW8uuunXI|350}}</center> | ||
Aktuelle Version vom 8. Februar 2021, 13:38 Uhr
Bisher haben wir zwei Multiplikationen bei Vektoren kennengelernt.
- die S-Multiplikation, die Multiplikation einer Zahl mit einem Vektor
- das Skalarprodukt, die Multiplikation zweier Vektoren, dessen Ergebnis eine Zahl ist.
| In der Physik haben Sie die Lorentzkraft bei der Bewegung geladener Teilchen in einem Magnetfeld kennengelernt. Mit der rechten-Hand-Regel konnte man die Richtung der Kraft auf die Teilchen bestimmen. Dazu verwendet man, dass die drei Finger Daumen - Zeigefinger - Mittelfinger auf natürliche Weise ein Rechtssystem, ein Koordinatensystem mit zueinander senkrecht stehenden Achsen, bilden. Dabei zeigt der Daumen in Bewegungsrichtung positver Ladungen, der Zeigefinger in Richtung des Magnetfeldes und der gestreckte Mittelfinger geht in Richtung der Lorentzkraft. In der Physik sind die Geschwindigkeit v, das Magnetfeld B und die Kraft F gerichtete Größen, d.h. sie haben eine Richtung einen Betrag. Man kann sie gut durch Vektoren darstellen. Hier wird also zu zwei gegebenen Vektoren ein dritter Vektor gesucht. |
a) 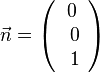
b) 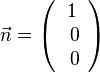
c) 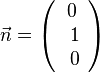
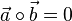 , also stehen
, also stehen  und
und 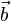 senkrecht zueinander. Dann findet man auch einen dritten Vektor, der jeweils senkrecht zu ihnen steht, z.B.
senkrecht zueinander. Dann findet man auch einen dritten Vektor, der jeweils senkrecht zu ihnen steht, z.B. 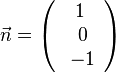 .
.|
Merke:
Zu den Vektoren Man spricht für Das Ergebnis des Kreuzprodukts
Der Betrag des Vektorprodukts ist dann gleich der Maßzahl des Flächeninhalts des von Der Flächeninhalt des von den Vektoren Die Begründungen zu den Eigenschaften lesen Sie bitte im Buch S. 116 nach. |
Beispiele:
1. Für 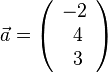 und
und 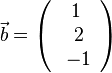 ist das Vektorprodukt
ist das Vektorprodukt 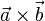 durch
durch 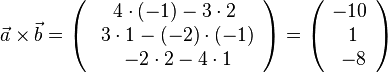 .
.
2. Für 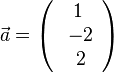 und
und 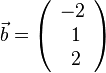 ist das Vektorprodukt
ist das Vektorprodukt 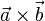 durch
durch 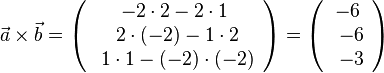 .
.
Es ist 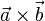 durch
durch 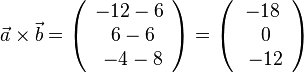 .
.
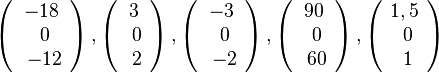 senkrecht auf
senkrecht auf 
a) 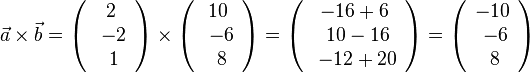
b) 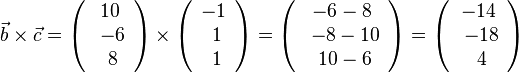
c) 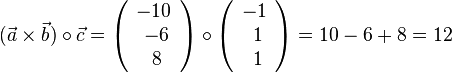
d) 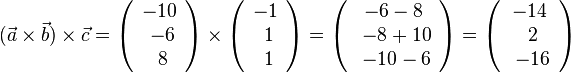
e) i) 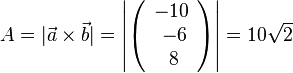
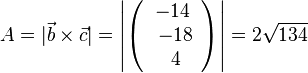
30px Merke
Der Flächeninhalt des von den Vektoren 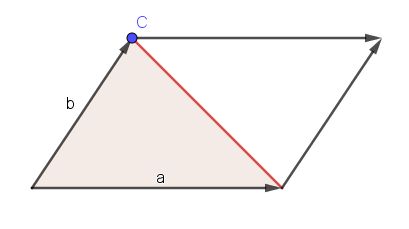 Der Flächeninhalt des von den Vektoren |
117/3
a) Raute, 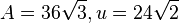
b) Quadrat, A = 50, u =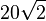
c) Rechteck, A = 50, u = 30
d) gleichschenkliges Trapez, A = 16
e) Parallelogramm, A = 29
117/4 a)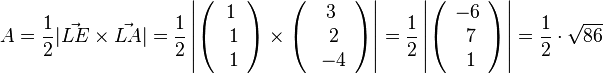 .
.
b) 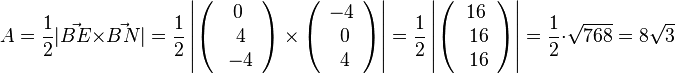 .
.
c) 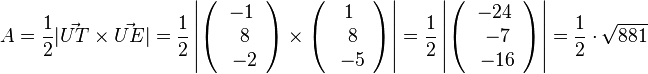 .
.
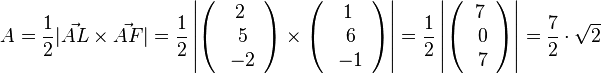 .
.
|
Merke:
Rechengesetze für das Vektorprodukt
|
Im Buch gibt es dazu Aufgaben s. 117/5,6. Man muss die Definitions des Kreuzprodukts verwenden und die Koordinaten so umformen, dass die Aussage richtig wird. Wer will kann sich daran versuchen. Ich korrigiere auch die Lösung.
118/7 Das Kreuzprodukt 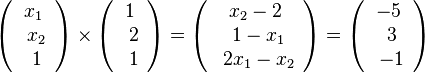 liefert ein Gleichungssystem aus drei Gleichungen mit zwei Unbekannten.
liefert ein Gleichungssystem aus drei Gleichungen mit zwei Unbekannten.
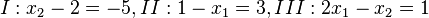
I ergibt 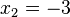 , II ergibt
, II ergibt 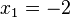 , Test in III liefert
, Test in III liefert 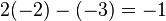 .
.
118/8 a) A(12;0;0), B(12;12;0), C(0;12;0), D(0;0;0), E(12;0;12), F(12;12;12), G(0;12;12), H(0;0;12)
b) K ist ein Punkt in der oberen Deckfläche k3=12, ebenso L wegen l3=12, und die anderen Koordinaten von K und L liegen zwischen 0 und 12.
M liegt auf der Kante [BF] und N auf der Kante [CG].(Koordinaten betrachten!)
P liegt nicht auf der Würfeloberfläche, da keine seiner Koordinaten 0 oder 12 ist. Q liegt nicht auf der Kugeloberfläche, da mit q2=13 der Punkt außerhalb des Würfels liegt.
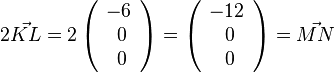 ; das Viereck KLMN ist ein Trapez, die Grundseiten haben die Längen 6cm und 12cm, die Höhe
; das Viereck KLMN ist ein Trapez, die Grundseiten haben die Längen 6cm und 12cm, die Höhe 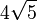 cm. Die Innenwinkel sind bei K 114,1°, bei L 102,6°, bei M 65,9° und bei N 77,4°.
cm. Die Innenwinkel sind bei K 114,1°, bei L 102,6°, bei M 65,9° und bei N 77,4°.
Der Flächeninhalt des Trapezes ergibt sich mit der Trapezformel zu 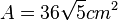 , die Umfangslänge
, die Umfangslänge 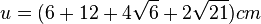
118/10 Es ist 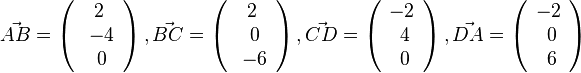 , also
, also 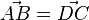 und
und 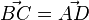 , also ist das Viereck ein Parallelogramm.
, also ist das Viereck ein Parallelogramm.
M erhält man durch 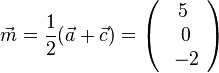 , also M(5;0;-2).
, also M(5;0;-2).
Der Flächeninhalt des Parallelogramms ist  .
.
Wegen der Volumenformel der Pyramide 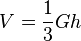 ist die Höhe der Pyramide h = 9.
ist die Höhe der Pyramide h = 9.
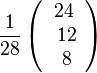 geht. Da man von M aus in zwei entgegengesetzte Richtungen gehen kann, schreibt sie +/- .
geht. Da man von M aus in zwei entgegengesetzte Richtungen gehen kann, schreibt sie +/- .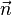 heraus, der mit den zwei Vektoren
heraus, der mit den zwei Vektoren 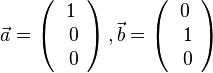 , b)
, b) 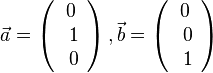 , c)
, c) 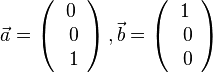 , d)
, d) 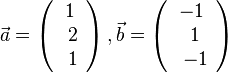

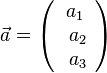 und
und 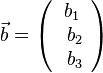 bildet man das Vektorprodukt
bildet man das Vektorprodukt 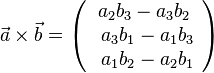 .
.
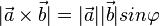 , wobei
, wobei  der Winkel zwischen den Vektoren
der Winkel zwischen den Vektoren 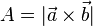
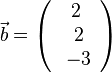 senkrecht stehen.
senkrecht stehen.
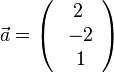 ,
, 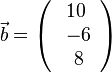 und
und 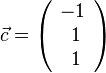
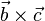
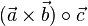
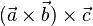
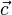 aufgespannten Parallelogramms.
aufgespannten Parallelogramms.
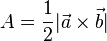 .
.
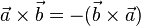
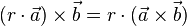
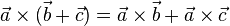 Distributivgesetz
Distributivgesetz

