|
|
| Zeile 21: |
Zeile 21: |
| | | | |
| | f) <math> \frac{1}{2}(x-1)^2 - 1= -0,5x + 2,5</math> Multipliziert man die Gleichung mit 2, dann fällt der Bruch <math>\frac{1}{2}</math> weg und man hat <math>(x^2-2x+1)-2=-x + 5</math>. Diese Gleichung auf die Form einer quadratischen Gleichung gebracht ergibt <math>x^2 - x - 6 = 0</math> mit den Lösungen <math>x_=-2, x_2 = 3</math><br> | | f) <math> \frac{1}{2}(x-1)^2 - 1= -0,5x + 2,5</math> Multipliziert man die Gleichung mit 2, dann fällt der Bruch <math>\frac{1}{2}</math> weg und man hat <math>(x^2-2x+1)-2=-x + 5</math>. Diese Gleichung auf die Form einer quadratischen Gleichung gebracht ergibt <math>x^2 - x - 6 = 0</math> mit den Lösungen <math>x_=-2, x_2 = 3</math><br> |
| − | r(-2;3,5) und T(3;1), <math>\bar {RT}=\sqrt {5^2+2,5^2}=\sqrt{31,25}=\sqrt{\frac{125}{4}}=\frac{5}{2}\sqrt 5 \approx 5,6</math> }}
| + | R(-2;3,5) und T(3;1), <math>\bar {RT}=\sqrt {5^2+2,5^2}=\sqrt{31,25}=\sqrt{\frac{125}{4}}=\frac{5}{2}\sqrt 5 \approx 5,6</math> }} |
| | | | |
| | {{Aufgaben-blau|2|2=Gemeinsame Punkte zweier Parabeln: Buch S. 100 / 7 }} | | {{Aufgaben-blau|2|2=Gemeinsame Punkte zweier Parabeln: Buch S. 100 / 7 }} |
Version vom 18. Februar 2021, 11:23 Uhr
Gemeinsame Punkte von Funktionsgraphen
 Merke
Gemeinsame Punkte von Funktionsgraphen findet man, indem man die Funktionsterme gleichsetzt und die Gleichung nach x auflöst.
|

Aufgabe 1
Gemeinsame Punkte einer Parabel mit einer Geraden: Buch S. 100 / 4
[Lösung anzeigen][Lösung ausblenden]

Aufgabe 2
Gemeinsame Punkte zweier Parabeln: Buch S. 100 / 7
[Lösung anzeigen][Lösung ausblenden]
a)Die beiden Parabeln haben gemeinsame Punkte, da P2 schlanker als P1 ist und ihren Scheitel unterhalb vom Scheitel von P1 hat.
b) P1 ist nach oben geöffnet und P2 ist nach unten geöffnet und P2 hat ihren Scheitel oberhalb des Scheitels von P1, also müssen sich die beiden Parabeln schneiden.
c) P1 hat ihren Scheitel bei (0;0) und ist die Normalparabel, also nach oben geöffnet. P2 hat ihren Scheitel bei (2;-4) und ist nach unten geöffnet. Die beiden Parabeln können sich nicht schneiden.
d) P1 hat ihren Scheitel bei (1;0) und ist nach oben geöffnet, P2 bei (-1;0) und ist nachunten geöffnet. Da beide Scheitel den gleichen y-Wert 0 haben und verschiedene x-Werte, können sich die beiden Parabeln nicht schneiden.
e) P1 ist die Normalparabel, P2 ist eine schlankere Parabel mit Scheitel (0;1) und beide sind nach oben geöffnet, also können sie sich nicht schneiden.
f) P1 ist einen nach unten geöffnete weite Parabel mit Scheitel (0;1), P2 ist nach oben geöffnet mit Scheitel (0;-4). Wegen -4 < 0 schneiden sich die beiden Parabeln.
Rechnungen für a, b, f
a)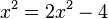 liefert
liefert 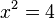 mit den zwei Lösungen
mit den zwei Lösungen 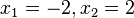
Die Schnittpunkte R(-2;4) und T(2;4) bilden mit den Scheiteln (0;0) und (0;-4) ein Viereck mit einer Symmetrieachse.
b) 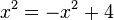 liefert
liefert 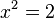 mit den zwei Lösungen
mit den zwei Lösungen 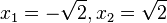 .
.
Die Schnittpunkte 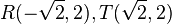 bilden mit den zwei Scheiteln (0;0) und (0;4) ein Quadrat mit 4 Symmetrieachsen. Die Seitenlänge des Quadrats ist
bilden mit den zwei Scheiteln (0;0) und (0;4) ein Quadrat mit 4 Symmetrieachsen. Die Seitenlänge des Quadrats ist 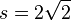 , sein Flächeninhalt
, sein Flächeninhalt 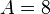 .
.
f) 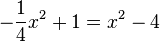 liefert
liefert 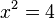 mit den zwei Lösungen
mit den zwei Lösungen 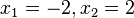 .
.
Die Schnittpunkte R(-2,0), T(2,0) bilden mit den zwei Scheiteln (0;1) und (0;-4) ein Drachenviereck mit einer Symmetrieachse.
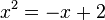 liefert eine quadratische Gleichung
liefert eine quadratische Gleichung 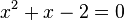 . Die Gleichung lässt sich in Linearfaktoren zerlegen
. Die Gleichung lässt sich in Linearfaktoren zerlegen 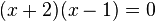 mit den zwei Lösungen
mit den zwei Lösungen 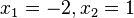 .
. 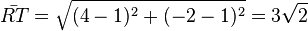 .
.
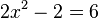 liefert
liefert 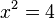 mit den Lösungen
mit den Lösungen 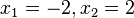 .
. 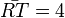
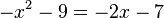 liefert
liefert 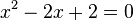 . Die Diskriminante D dieser Gleichung ist D = (-2)2 - 4·2 = 4 - 8 = -4 < 0. Also hat die Gleichung keine Lösung und die Graphen keine gemeinsamen Punkte.
. Die Diskriminante D dieser Gleichung ist D = (-2)2 - 4·2 = 4 - 8 = -4 < 0. Also hat die Gleichung keine Lösung und die Graphen keine gemeinsamen Punkte.
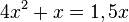 liefert
liefert 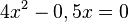 . Man kann 4x ausklammern:
. Man kann 4x ausklammern: 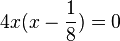 hat die zwei Löungen
hat die zwei Löungen 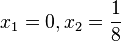 .
. 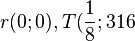 und die Streckenlänge
und die Streckenlänge 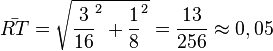
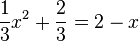 liefert
liefert 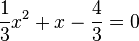 . Die linke Seite lässt sich umformen in
. Die linke Seite lässt sich umformen in 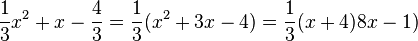 und man löst die Gleichung
und man löst die Gleichung 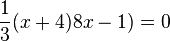 mit den zwei Lösungen
mit den zwei Lösungen 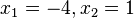
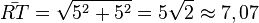 .
.
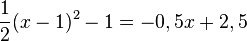 Multipliziert man die Gleichung mit 2, dann fällt der Bruch
Multipliziert man die Gleichung mit 2, dann fällt der Bruch  weg und man hat
weg und man hat 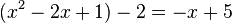 . Diese Gleichung auf die Form einer quadratischen Gleichung gebracht ergibt
. Diese Gleichung auf die Form einer quadratischen Gleichung gebracht ergibt 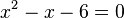 mit den Lösungen
mit den Lösungen 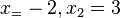
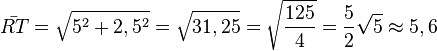
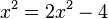 liefert
liefert 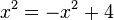 liefert
liefert 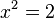 mit den zwei Lösungen
mit den zwei Lösungen 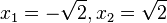 .
. 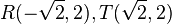 bilden mit den zwei Scheiteln (0;0) und (0;4) ein Quadrat mit 4 Symmetrieachsen. Die Seitenlänge des Quadrats ist
bilden mit den zwei Scheiteln (0;0) und (0;4) ein Quadrat mit 4 Symmetrieachsen. Die Seitenlänge des Quadrats ist 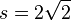 , sein Flächeninhalt
, sein Flächeninhalt 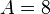 .
.
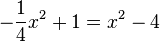 liefert
liefert 
