M9 Anwendungen und Aufgaben zu quadratischen Funktionen: Unterschied zwischen den Versionen
Aus RSG-Wiki
(→Gemeinsame Punkte von Funktionsgraphen) |
(→Gemeinsame Punkte von Funktionsgraphen) |
||
| Zeile 1: | Zeile 1: | ||
| + | __NOCACHE__ | ||
=Gemeinsame Punkte von Funktionsgraphen= | =Gemeinsame Punkte von Funktionsgraphen= | ||
| Zeile 34: | Zeile 35: | ||
Rechnungen für a, b, f<br> | Rechnungen für a, b, f<br> | ||
a)<math>x^2 = 2x^2 -4</math> liefert <math>x^2=4</math> mit den zwei Lösungen <math>x_1=-2, x_2=2</math><br> | a)<math>x^2 = 2x^2 -4</math> liefert <math>x^2=4</math> mit den zwei Lösungen <math>x_1=-2, x_2=2</math><br> | ||
| − | Die Schnittpunkte R(-2;4) und T(2;4) bilden mit den Scheiteln (0;0) und (0;-4) ein Viereck | + | Die Schnittpunkte R(-2;4) und T(2;4) bilden mit den Scheiteln (0;0) und (0;-4) ein Viereck. |
b) <math>x^2 = -x^2 + 4</math> liefert <math>x^2 = 2</math> mit den zwei Lösungen <math>x_1=-\sqrt 2, x_2 = \sqrt 2</math>. <br> | b) <math>x^2 = -x^2 + 4</math> liefert <math>x^2 = 2</math> mit den zwei Lösungen <math>x_1=-\sqrt 2, x_2 = \sqrt 2</math>. <br> | ||
| − | Die Schnittpunkte <math>R(-\sqrt 2 , 2), T(\sqrt 2 , 2)</math> bilden mit den zwei Scheiteln (0;0) und (0;4) | + | Die Schnittpunkte <math>R(-\sqrt 2 , 2), T(\sqrt 2 , 2)</math> bilden mit den zwei Scheiteln (0;0) und (0;4) eine Raute mit 2 Symmetrieachsen. Ihr Flächeninhalt ist <math>A = 4 \sqrt 2</math>. |
f) <math>-\frac{1}{4} x^2 + 1 = x^2 - 4</math> liefert <math>x^2 =4</math> mit den zwei Lösungen <math>x_1= -2, x_2 = 2</math>.<br> | f) <math>-\frac{1}{4} x^2 + 1 = x^2 - 4</math> liefert <math>x^2 =4</math> mit den zwei Lösungen <math>x_1= -2, x_2 = 2</math>.<br> | ||
| − | Die Schnittpunkte R(-2,0), T(2,0) bilden mit den zwei Scheiteln (0;1) und (0;-4) ein Drachenviereck mit einer Symmetrieachse. }} | + | Die Schnittpunkte R(-2,0), T(2,0) bilden mit den zwei Scheiteln (0;1) und (0;-4) ein Drachenviereck mit einer Symmetrieachse. |
| + | |||
| + | Im folgenden Applet kannst du die Parabeln zu den Aufgaben und gegebenenfalls die Vierecke dir anzeigen lassen. }} | ||
| + | |||
| + | <center><ggb_applet height="700" width="900" filename="100-7.ggb" /></center> | ||
| + | |||
| + | {{Aufgaben-blau|3|2=Gemeinsame Punkte zweier Funktionsgraphen: Buch S. 101 / 8 }} | ||
| + | |||
| + | {{Lösung versteckt|1= | ||
| + | }} | ||
Version vom 18. Februar 2021, 12:19 Uhr
Gemeinsame Punkte von Funktionsgraphen
|
Gemeinsame Punkte von Funktionsgraphen findet man, indem man die Funktionsterme gleichsetzt und die Gleichung nach x auflöst. |
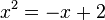 liefert eine quadratische Gleichung
liefert eine quadratische Gleichung 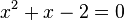 . Die Gleichung lässt sich in Linearfaktoren zerlegen
. Die Gleichung lässt sich in Linearfaktoren zerlegen 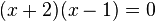 mit den zwei Lösungen
mit den zwei Lösungen 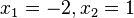 .
. 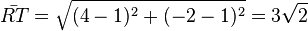 .
.
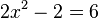 liefert
liefert 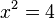 mit den Lösungen
mit den Lösungen 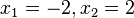 .
. 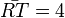
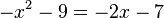 liefert
liefert 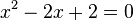 . Die Diskriminante D dieser Gleichung ist D = (-2)2 - 4·2 = 4 - 8 = -4 < 0. Also hat die Gleichung keine Lösung und die Graphen keine gemeinsamen Punkte.
. Die Diskriminante D dieser Gleichung ist D = (-2)2 - 4·2 = 4 - 8 = -4 < 0. Also hat die Gleichung keine Lösung und die Graphen keine gemeinsamen Punkte.
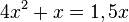 liefert
liefert 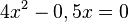 . Man kann 4x ausklammern:
. Man kann 4x ausklammern: 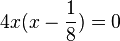 hat die zwei Löungen
hat die zwei Löungen 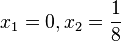 .
. 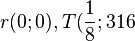 und die Streckenlänge
und die Streckenlänge 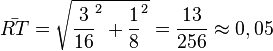
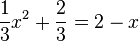 liefert
liefert 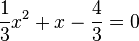 . Die linke Seite lässt sich umformen in
. Die linke Seite lässt sich umformen in 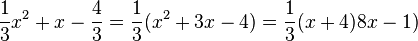 und man löst die Gleichung
und man löst die Gleichung 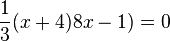 mit den zwei Lösungen
mit den zwei Lösungen 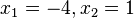
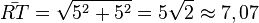 .
.
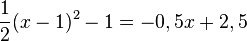 Multipliziert man die Gleichung mit 2, dann fällt der Bruch
Multipliziert man die Gleichung mit 2, dann fällt der Bruch  weg und man hat
weg und man hat 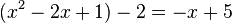 . Diese Gleichung auf die Form einer quadratischen Gleichung gebracht ergibt
. Diese Gleichung auf die Form einer quadratischen Gleichung gebracht ergibt 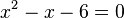 mit den Lösungen
mit den Lösungen 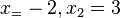
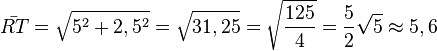
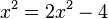 liefert
liefert 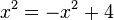 liefert
liefert 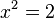 mit den zwei Lösungen
mit den zwei Lösungen 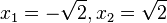 .
. 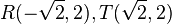 bilden mit den zwei Scheiteln (0;0) und (0;4) eine Raute mit 2 Symmetrieachsen. Ihr Flächeninhalt ist
bilden mit den zwei Scheiteln (0;0) und (0;4) eine Raute mit 2 Symmetrieachsen. Ihr Flächeninhalt ist 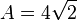 .
.
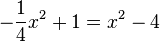 liefert
liefert 
