M11 Aufgaben und Anwendungen der Vektorrechnung: Unterschied zwischen den Versionen
Aus RSG-Wiki
(Die Seite wurde neu angelegt: „{{Aufgaben-blau|1|2=Buch S. 102 / 1 <br> Buch S. 120 / 4 <br> Buch S. 121 / 5 }} {{Lösung versteckt|1=1. Gesucht sind die Punktkoordinaten, diese werden …“) |
|||
| (5 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{Aufgaben-blau|1|2=Buch S. | + | {{Aufgaben-blau|1|2=Buch S. 120 / 1 <br> |
Buch S. 120 / 4 <br> | Buch S. 120 / 4 <br> | ||
Buch S. 121 / 5 }} | Buch S. 121 / 5 }} | ||
| Zeile 36: | Zeile 36: | ||
Das Symmetriezentrum ist nun (-2;0) und der Verschiebungsvektor <math> \vec v = \left ( \begin{array}{c} -2 \\\ 0 \end{array}\right)</math> . Der grüne Graph der Funktion <math>f</math> wird um 2 nach links verschoben und man erhält den blauen Graph der Funktion <math>f_2</math>. | Das Symmetriezentrum ist nun (-2;0) und der Verschiebungsvektor <math> \vec v = \left ( \begin{array}{c} -2 \\\ 0 \end{array}\right)</math> . Der grüne Graph der Funktion <math>f</math> wird um 2 nach links verschoben und man erhält den blauen Graph der Funktion <math>f_2</math>. | ||
<center>[[Datei:121-10.jpg|400px]]</center>}} | <center>[[Datei:121-10.jpg|400px]]</center>}} | ||
| + | |||
| + | {{Aufgaben-blau|3|2=Bestimmen Sie die Koordinaten <br> | ||
| + | 1. des Mittelpunkts der Strecke [AB] mit <br> | ||
| + | a) A(0;3;-4) und B(-6;1;-2)<br> | ||
| + | b) A(8;0,5;-5) und B(-3;1,5;-1)<br> | ||
| + | 2. den Schwerpunkt des Dreiecks ABC mit A(-2;0;3), B(5;2;1) und C(0;4;2) }} | ||
| + | |||
| + | {{Lösung versteckt|1=1a) <math>\vec m = \frac{1}{2}(\vec a + \vec b) = \frac{1}{2} \cdot \left [ \left ( \begin{array}{c} 0 \\\ 3 \\\ -4 \end{array}\right) + \left ( \begin{array}{c} -6 \\\ 1 \\\ -2 \end{array}\right) \right ] = \left ( \begin{array}{c} -3 \\\ 2 \\\ -3 \end{array}\right)</math><br> | ||
| + | b) <math>\vec m = \frac{1}{2}(\vec a + \vec b) = \frac{1}{2} \cdot \left [ \left ( \begin{array}{c} 8 \\\ 0,5 \\\ -5 \end{array}\right) + \left ( \begin{array}{c} -3 \\\ 1,5 \\\ -1 \end{array}\right) \right ] = \left ( \begin{array}{c} 2,5 \\\ 1 \\\ -3 \end{array}\right)</math> und M(2,5;1;-3)<br> | ||
| + | |||
| + | 2. <math>\vec s=\frac{1}{3}(\vec a + \vec b + \vec c) = \frac{1}{3} \left [ \left ( \begin{array}{c} -2 \\\ 0 \\\ 3 \end{array}\right) + \left ( \begin{array}{c} 5 \\\ 2 \\\ 1 \end{array}\right) + \left ( \begin{array}{c} 0 \\\ 4 \\\ 2 \end{array}\right) \right ]= \frac{1}{3} \left ( \begin{array}{c} 3 \\\ 6 \\\ 6 \end{array}\right) = \left ( \begin{array}{c} 1 \\\ 2 \\\ 2 \end{array}\right)</math> und S(1;2;2) }} | ||
| + | |||
| + | {{Aufgaben-blau|4|2=Buch S. 123 / 29a }} | ||
| + | |||
| + | {{Lösung versteckt|1=Das Viereck ABCD bildet die Grundfläche der Pyramide. Da in der Volumenformel der Pyramide <math>V=\frac{1}{3}Gh</math> der Flächeninhalt der Grundfläche vorkommt. soll zuerst G berechnet werden.<br> | ||
| + | <math>\vec {AB}=\vec b + \vec a = \left ( \begin{array}{c} 5 \\\ 0 \\\ -1 \end{array}\right) - \left ( \begin{array}{c} 1 \\\ 2 \\\ 3 \end{array}\right) = \left ( \begin{array}{c} 4 \\\ -2 \\\ -4 \end{array}\right), \vec {BC}= \left ( \begin{array}{c} -2 \\\ 4 \\\ -4 \end{array}\right), \vec {CD}= \left ( \begin{array}{c} -4 \\\ 2 \\\ 4 \end{array}\right), \vec {DA}= \left ( \begin{array}{c} 2 \\\ -4 \\\ 4 \end{array}\right)</math><br> | ||
| + | Hier sieht man, dass <math>\vec {AB} = -\vec {CD} = \vec {DC}, \vec {BC}=-\vec {DA}=\vec {AD}</math> ist, das Viereck ist also ein Parallelogramm. Es ist weiterhin <math>|\vec {AB}| = \sqrt {4^2 + (-2)^2+(-4)^2}=6=|\vec {BC}|=|\vec {CD}|=|\vec {DA}|</math>. Also ist das Viereck eine Raute.<br> | ||
| + | Wegen <math> \vec {AB} \circ \vec {BC}=-8-8+16=0</math> ist der Winkel bei B ein 90<sup>o</sup>-Winkel. Also ist das Viereck ein Quadrat. Sein Flächeninhalt ist dann G = 36. <br> | ||
| + | Aus der Volumenformel <math>V=\frac{1}{3}Gh</math> kann man nun die Länge der Pyramidenhöhe h bestimmen. <math>h = \frac{3V}{G} = \frac{3\cdot 72}{36}=6</math>.<br> | ||
| + | Mit dem Vektorprodukt hätte man auch den Flächeninhalt der Grundfläche G bestimmen können. Man erhält auch hier 36 (wird weiter unten noch berechnet). | ||
| + | |||
| + | Der Mittelpunkt M des Quadrats ist der Höhenfußpunkt der Pyramide. M ist auch der Schnittpunkt der Diagonalen des Quadrats, bzw. der Mittelpunkt einer Quadratdiagonalen. <br> | ||
| + | Es ist <math>\vec m = \frac{1}{2}(\vec a + \vec c)=\frac{1}{2} \left[ \left ( \begin{array}{c} 1 \\\ 2 \\\ 3 \end{array}\right) + \left ( \begin{array}{c} 3 \\\ 4 \\\ -5 \end{array}\right) \right ] = \left ( \begin{array}{c} 2 \\\ 3 \\\ -1 \end{array}\right)</math> und M(2;3;-1).<br> | ||
| + | Nun muss man senkrecht zu G von M aus 6 Einheiten nach "oben" oder "unten" gehen um zu S zu kommen. Dazu braucht man einen Vektor <math>\vec v</math>, der senkrecht zur Grundfläche steht. Einen solchen Vektor erhält man, wenn man das Vektorprodukt <math>\vec {AB} \times \vec {AD}</math> bestimmt. Es ist <math>\vec {AB} \times \vec {AD} = \left ( \begin{array}{c} 4 \\\ -2 \\\ -4 \end{array}\right) \times \left ( \begin{array}{c} -2 \\\ 4 \\\ -4 \end{array}\right) = \left ( \begin{array}{c} 24 \\\ 24 \\\ 12 \end{array}\right)</math><br> | ||
| + | Der Betrag des Vektors <math>\vec v</math> ist <math>|\vec v|=\left |\left ( \begin{array}{c} 24 \\\ 24 \\\ 12 \end{array}\right)\right | =36</math><br> | ||
| + | Der Einheitsvektor zu <math>\vec {v^1}</math> zum Vektor <math>\vec v=\left ( \begin{array}{c} 24 \\\ 24 \\\ 12 \end{array}\right)</math> ist <math>\vec {v^1}=\frac{1}{36}\left ( \begin{array}{c} 24 \\\ 24 \\\ 12 \end{array}\right)= \frac{1}{3}\left ( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right)</math> | ||
| + | |||
| + | Nun muss man die Pyramidenspitze S bestimmen. Von M aus geht man 6 Einheiten in Richtung des Einheitsvektors <math>\vec {v^1}</math>, also <math>\vec {MS}=6\cdot \frac{1}{3} \left ( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right) = \left ( \begin{array}{c} 4 \\\ 4 \\\ 2 \end{array}\right)</math>.<br> | ||
| + | Die Spitze S hat den Ortsvektor <math>\vec s</math> und es ist <math>\vec s = \vec m + \vec {MS}=\left ( \begin{array}{c} 2 \\\ 3 \\\ -1 \end{array}\right) + \left ( \begin{array}{c} 4 \\\ 4 \\\ 2 \end{array}\right) = \left ( \begin{array}{c} 6 \\\ 7 \\\ 1 \end{array}\right)</math> und S(6;7;1) | ||
| + | |||
| + | Man hätte von M aus auch in die Richtung von <math>-\frac{1}{3}\left ( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right)</math> gehen können. Dann geht man von M aus 6 Einheiten in Richtung dieses Einheitsvektors und bekommt dann <math>\vec {MS'}=-6\cdot \frac{1}{3} \left ( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right) = \left ( \begin{array}{c} -4 \\\ -4 \\\ -2 \end{array}\right)</math>.<br> | ||
| + | S' hat dann die Koordinaten S'(-2;-1;-3).}} | ||
| + | |||
| + | {{Aufgaben-blau|5|2=Buch S. 124 / 33<br> | ||
| + | Buch S. 124 / 35 }} | ||
| + | |||
| + | {{Lösung versteckt|1=1124/33 a)<math>\vec {TR}=\vec r + \vec t = \left ( \begin{array}{c} 1 \\\ 6 \\\ -1 \end{array}\right) - \left ( \begin{array}{c} 3 \\\ 2 \\\ 1 \end{array}\right) = \left ( \begin{array}{c} -2 \\\ 4 \\\ -2 \end{array}\right), \vec {RE}= \left ( \begin{array}{c} -2 \\\ -2 \\\ 4 \end{array}\right), \vec {ET}= \left ( \begin{array}{c} 4 \\\ -2 \\\ -2 \end{array}\right)</math><br> | ||
| + | <math>|\vec {TR}| = \sqrt {(-2)^2 + 4^2+(-2)^2}=\sqrt {24} = 2 \sqrt 6=|\vec {RE}|=|\vec {ET}|</math>, also ist das Dreieck TRE gleichseitig. Seine Umfangslänge ist <math>u = 3\cdot 2 \sqrt 6 = 6 \sqrt 6</math> und sein Flächeninhalt <math> A = \frac{1}{2}gh=\frac{1}{2}\cdot g \cdot \frac{g}{2}\sqrt 3=\frac{1}{2}\cdot 2 \sqrt 6 \cdot \frac{2 \sqrt 6}{2}\sqrt 3 = 6 \sqrt 3</math>. | ||
| + | |||
| + | b) Um zu zeigen, dass die drei Punkte T, R, E gleichweit von M entfernt sind, muss man die Beträge der Vektoren <math>\vec {TM}, \vec {RM}, \vec {EM}</math> berechnen. <br> | ||
| + | Es ist <math>\vec {TM}= \left ( \begin{array}{c} -2 \\\ 2 \\\ 0 \end{array}\right), \vec {RM}=\left ( \begin{array}{c} 0 \\\ -2 \\\ 2 \end{array}\right), \vec {EM}=\left ( \begin{array}{c} 2 \\\ 0 \\\ -2 \end{array}\right)</math> und <math>|\vec {TM}|=\sqrt {(-2)^2+2^2+0^2}=2\sqrt 2 = |\vec {RM}|=|\vec {EM}|</math>.<br> | ||
| + | T, R und E liegen auf einer Kugel um M mit Radius <math> r=2 \sqrt 2</math>. Die Koordinatengleichung der Kugel lautet <math>(x_1-1)^2 + (x_2-4)^2 + (x_3-1)^2 =8</math>.<br> | ||
| + | Die Inhalt der Oberfläche ist <math> O = 4 \pi r^2 = 32 \pi \approx 100,5</math>, das Volumen ist <math>V=\frac{4}{3}r^3\pi=\frac{4}{3}(2\sqrt 2)^3 \pi=\frac{64}{3}\sqrt 2 \pi \approx 94,8</math> | ||
| + | |||
| + | |||
| + | 124/35 <math>\vec {AB}=\vec b + \vec a = \left ( \begin{array}{c} 7 \\\ 10 \\\ 4 \end{array}\right) - \left ( \begin{array}{c} 5 \\\ 5 \\\ 4 \end{array}\right) = \left ( \begin{array}{c} 2 \\\ 5 \\\ 0 \end{array}\right), \vec {BC}= \left ( \begin{array}{c} 0 \\\ 0 \\\ -4 \end{array}\right), \vec {CD}= \left ( \begin{array}{c} -2 \\\ -5 \\\ 0 \end{array}\right), \vec {DA}= \left ( \begin{array}{c} 0 \\\ 0 \\\ 4 \end{array}\right)</math><br> | ||
| + | Hier sieht man, dass <math>\vec {AB} = -\vec {CD} = \vec {DC}, \vec {BC}=-\vec {DA}=\vec {AD}</math> ist, das Viereck ist also ein Parallelogramm. <br> | ||
| + | Berechnet man den Winkel bei A, dann ist <math>\vec {AB} \circ \vec {AD}=\left ( \begin{array}{c} 2 \\\ 5 \\\ 0 \end{array}\right) \circ \left ( \begin{array}{c} 0 \\\ 0 \\\ -4 \end{array}\right) = 0 + 0 + 0 = 0</math>, also ist bei A ein 90<sup>o</sup>-Winkel und das Parallelogramm ist ein Rechteck mit den Seitenlängen <math>l = \sqrt {29}, b = 4</math>. | ||
| + | |||
| + | Die Volumina der beiden Pyramiden ABCDS<sub>1</sub> und ABCDS<sub>2</sub> berechnet man mittels der Volumenformel <math>V=\frac{1}{3}|(\vec {AB} \times \vec {AD}) \circ \vec {AS}|</math><br> | ||
| + | Es ist <math>V_1=\frac{1}{3}|(\vec {AB} \times \vec {AD}) \circ \vec {AS_1}|=\frac{1}{3} \left | \left [ \left ( \begin{array}{c} 2 \\\ 5 \\\ 0 \end{array}\right) \times \left ( \begin{array}{c} 0 \\\ 0 \\\ -4 \end{array}\right) \right ] \circ \ \left ( \begin{array}{c} 2 \\\ 2,1 \\\ -2 \end{array}\right) \right | = =\frac{1}{3} \left | \left ( \begin{array}{c} -20 \\\ 8 \\\ 0 \end{array}\right) \circ \left ( \begin{array}{c} 2 \\\ 2,1 \\\ -2 \end{array}\right) \right |=| \frac{1}{3} \cdot \frac{-116}{5} | = 7\frac{11}{15}</math> und <br> | ||
| + | Es ist <math>V_2=\frac{1}{3}|(\vec {AB} \times \vec {AD}) \circ \vec {AS_2}|=\frac{1}{3} \left | \left [ \left ( \begin{array}{c} 2 \\\ 5 \\\ 0 \end{array}\right) \times \left ( \begin{array}{c} 0 \\\ 0 \\\ -4 \end{array}\right) \right ] \circ \ \left ( \begin{array}{c} 0 \\\ 2,9 \\\ -2 \end{array}\right) \right | = =\frac{1}{3} \left | \left ( \begin{array}{c} -20 \\\ 8 \\\ 0 \end{array}\right) \circ \left ( \begin{array}{c} 0 \\\ 2,9 \\\ -2 \end{array}\right) \right |=| \frac{1}{3} \cdot \frac{116}{5} | = 7\frac{11}{15}</math><br> | ||
| + | Das Volumen der Doppelpyramide ist <math> V = V_1+V_2=15\frac{7}{15}</math>. }} | ||
Aktuelle Version vom 22. Februar 2021, 14:40 Uhr
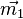 des Mittelpunktes der Strecke [DB] hat man die Formel
des Mittelpunktes der Strecke [DB] hat man die Formel 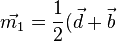 . Dies liefert dann aie Koordinaten des Schnittpunktes.
. Dies liefert dann aie Koordinaten des Schnittpunktes. 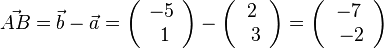 und
und 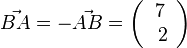
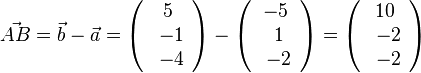 und
und 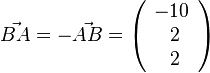
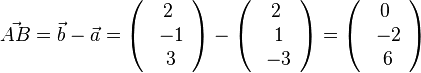 und
und 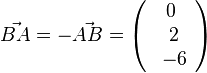
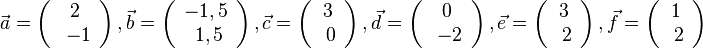
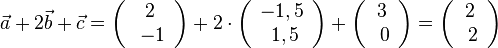
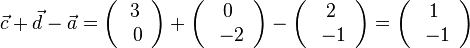
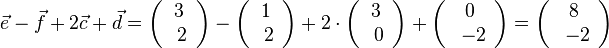
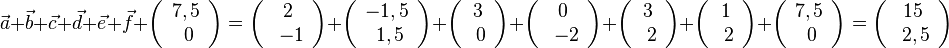
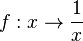 D=R\{0},
D=R\{0},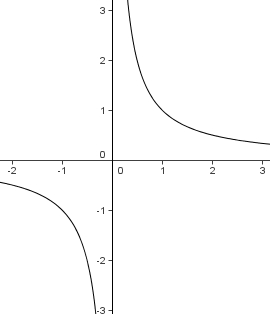
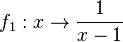 hat die Definitionslücke bei x = 1. Also wird der Graph der Funktion
hat die Definitionslücke bei x = 1. Also wird der Graph der Funktion 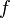 um 1 nach rechts in x-Richtung verschoben.
um 1 nach rechts in x-Richtung verschoben. 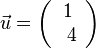 . Der grüne Graph der Funktion
. Der grüne Graph der Funktion 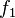 .
.
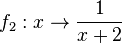 hat die Definitionslücke bei x = -2. Also wird der Graph der Funktion
hat die Definitionslücke bei x = -2. Also wird der Graph der Funktion 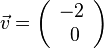 . Der grüne Graph der Funktion
. Der grüne Graph der Funktion 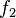 .
.
![\vec m = \frac{1}{2}(\vec a + \vec b) = \frac{1}{2} \cdot \left [ \left ( \begin{array}{c} 0 \\\ 3 \\\ -4 \end{array}\right) + \left ( \begin{array}{c} -6 \\\ 1 \\\ -2 \end{array}\right) \right ] = \left ( \begin{array}{c} -3 \\\ 2 \\\ -3 \end{array}\right)](/images/math/2/3/2/232ed63bc2c5edc99385002362086b10.png)
![\vec m = \frac{1}{2}(\vec a + \vec b) = \frac{1}{2} \cdot \left [ \left ( \begin{array}{c} 8 \\\ 0,5 \\\ -5 \end{array}\right) + \left ( \begin{array}{c} -3 \\\ 1,5 \\\ -1 \end{array}\right) \right ] = \left ( \begin{array}{c} 2,5 \\\ 1 \\\ -3 \end{array}\right)](/images/math/2/1/d/21dc216569e9be01268e6810879107c2.png) und M(2,5;1;-3)
und M(2,5;1;-3)![\vec s=\frac{1}{3}(\vec a + \vec b + \vec c) = \frac{1}{3} \left [ \left ( \begin{array}{c} -2 \\\ 0 \\\ 3 \end{array}\right) + \left ( \begin{array}{c} 5 \\\ 2 \\\ 1 \end{array}\right) + \left ( \begin{array}{c} 0 \\\ 4 \\\ 2 \end{array}\right) \right ]= \frac{1}{3} \left ( \begin{array}{c} 3 \\\ 6 \\\ 6 \end{array}\right) = \left ( \begin{array}{c} 1 \\\ 2 \\\ 2 \end{array}\right)](/images/math/1/3/0/130511978b9e104386eecb504758b6fc.png) und S(1;2;2)
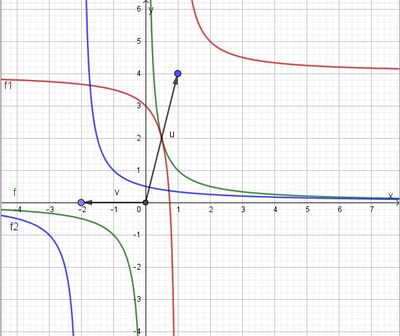
und S(1;2;2)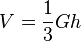 der Flächeninhalt der Grundfläche vorkommt. soll zuerst G berechnet werden.
der Flächeninhalt der Grundfläche vorkommt. soll zuerst G berechnet werden.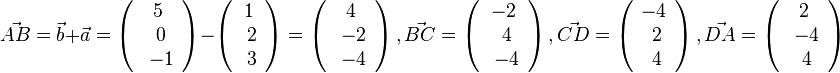
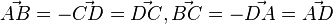 ist, das Viereck ist also ein Parallelogramm. Es ist weiterhin
ist, das Viereck ist also ein Parallelogramm. Es ist weiterhin 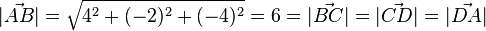 . Also ist das Viereck eine Raute.
. Also ist das Viereck eine Raute.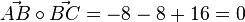 ist der Winkel bei B ein 90o-Winkel. Also ist das Viereck ein Quadrat. Sein Flächeninhalt ist dann G = 36.
ist der Winkel bei B ein 90o-Winkel. Also ist das Viereck ein Quadrat. Sein Flächeninhalt ist dann G = 36. 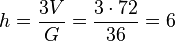 .
.![\vec m = \frac{1}{2}(\vec a + \vec c)=\frac{1}{2} \left[ \left ( \begin{array}{c} 1 \\\ 2 \\\ 3 \end{array}\right) + \left ( \begin{array}{c} 3 \\\ 4 \\\ -5 \end{array}\right) \right ] = \left ( \begin{array}{c} 2 \\\ 3 \\\ -1 \end{array}\right)](/images/math/6/0/3/603cf07814d38f9e69600a54a9e4eb0c.png) und M(2;3;-1).
und M(2;3;-1).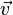 , der senkrecht zur Grundfläche steht. Einen solchen Vektor erhält man, wenn man das Vektorprodukt
, der senkrecht zur Grundfläche steht. Einen solchen Vektor erhält man, wenn man das Vektorprodukt 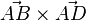 bestimmt. Es ist
bestimmt. Es ist 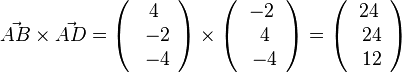
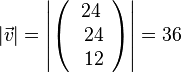
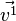 zum Vektor
zum Vektor 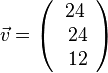 ist
ist 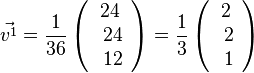
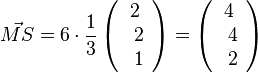 .
. und es ist
und es ist 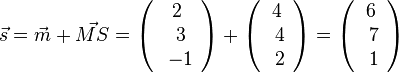 und S(6;7;1)
und S(6;7;1)
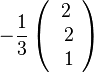 gehen können. Dann geht man von M aus 6 Einheiten in Richtung dieses Einheitsvektors und bekommt dann
gehen können. Dann geht man von M aus 6 Einheiten in Richtung dieses Einheitsvektors und bekommt dann 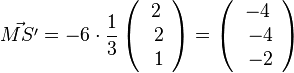 .
.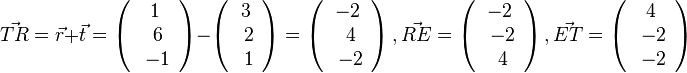
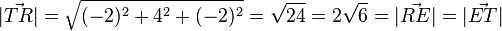 , also ist das Dreieck TRE gleichseitig. Seine Umfangslänge ist
, also ist das Dreieck TRE gleichseitig. Seine Umfangslänge ist 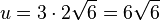 und sein Flächeninhalt
und sein Flächeninhalt 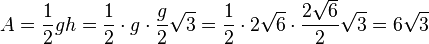 .
.
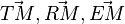 berechnen.
berechnen. 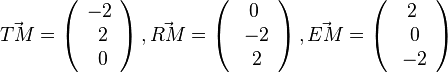 und
und 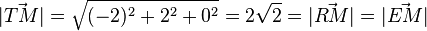 .
.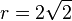 . Die Koordinatengleichung der Kugel lautet
. Die Koordinatengleichung der Kugel lautet 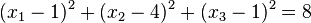 .
.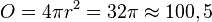 , das Volumen ist
, das Volumen ist 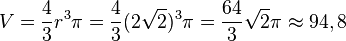
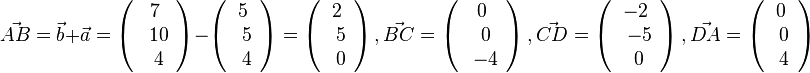
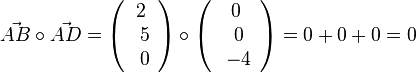 , also ist bei A ein 90o-Winkel und das Parallelogramm ist ein Rechteck mit den Seitenlängen
, also ist bei A ein 90o-Winkel und das Parallelogramm ist ein Rechteck mit den Seitenlängen 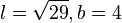 .
.
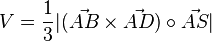
![V_1=\frac{1}{3}|(\vec {AB} \times \vec {AD}) \circ \vec {AS_1}|=\frac{1}{3} \left | \left [ \left ( \begin{array}{c} 2 \\\ 5 \\\ 0 \end{array}\right) \times \left ( \begin{array}{c} 0 \\\ 0 \\\ -4 \end{array}\right) \right ] \circ \ \left ( \begin{array}{c} 2 \\\ 2,1 \\\ -2 \end{array}\right) \right | = =\frac{1}{3} \left | \left ( \begin{array}{c} -20 \\\ 8 \\\ 0 \end{array}\right) \circ \left ( \begin{array}{c} 2 \\\ 2,1 \\\ -2 \end{array}\right) \right |=| \frac{1}{3} \cdot \frac{-116}{5} | = 7\frac{11}{15}](/images/math/b/3/4/b34734b58214be23e7ea9a11d58a277c.png) und
und ![V_2=\frac{1}{3}|(\vec {AB} \times \vec {AD}) \circ \vec {AS_2}|=\frac{1}{3} \left | \left [ \left ( \begin{array}{c} 2 \\\ 5 \\\ 0 \end{array}\right) \times \left ( \begin{array}{c} 0 \\\ 0 \\\ -4 \end{array}\right) \right ] \circ \ \left ( \begin{array}{c} 0 \\\ 2,9 \\\ -2 \end{array}\right) \right | = =\frac{1}{3} \left | \left ( \begin{array}{c} -20 \\\ 8 \\\ 0 \end{array}\right) \circ \left ( \begin{array}{c} 0 \\\ 2,9 \\\ -2 \end{array}\right) \right |=| \frac{1}{3} \cdot \frac{116}{5} | = 7\frac{11}{15}](/images/math/9/b/3/9b3653a219d996412d11f586a4e51190.png)
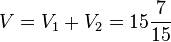 .
.
