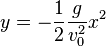Ph10 Der waagrechte Wurf: Unterschied zwischen den Versionen
Aus RSG-Wiki
(Die Seite wurde neu angelegt: „<center>{{#ev:youtube |WI-4kmNph2Q|350}}</center> {{Merksatz|MERK=Der '''waagrechte Wurf''' ist eine zweidimensionale Bewegung und setzt sich als Überlagerun…“) |
|||
| Zeile 8: | Zeile 8: | ||
{{Aufgaben-blau|1|2=Beschreibe mit einfachen Worten was ein waagrechter Wurf ist. }} | {{Aufgaben-blau|1|2=Beschreibe mit einfachen Worten was ein waagrechter Wurf ist. }} | ||
| − | {{Lösung versteckt|1= | + | {{Lösung versteckt|1=Bei einem waagrechter Wurf wirft man einen Körper waagrecht mit einer Anfangsgeschwindigkeit los. Er fliegt dann geradlinigen in x-Richtung mit konstanter Geschwindigkeit weiter, gleichzeitig wirkt auf ihn seine Gewichtskraft in y-Richtung. Von dieser wird er mit konstanter Beschleunigung nach unten beschleunigt (freier Fall). }} |
| − | <center>{{#ev:youtube |s3vi9St-Uh8|350}}</center> | + | |
| + | <center>{{#ev:youtube |s3vi9St-Uh8|350}}</center> | ||
{{Merksatz|MERK=Bewegungsgleichungen für den waagrechten Wurf | {{Merksatz|MERK=Bewegungsgleichungen für den waagrechten Wurf | ||
| Zeile 16: | Zeile 17: | ||
Eliminiert man die Variable t, dann erhält man für die Bahnkurve die Gleichung einer Parabel. Die Bahnkurve heißt '''Wurfparabel''', ihr Gleichung ist <br> | Eliminiert man die Variable t, dann erhält man für die Bahnkurve die Gleichung einer Parabel. Die Bahnkurve heißt '''Wurfparabel''', ihr Gleichung ist <br> | ||
| − | <center><math>y = -\frac{1}{2} \frac{g}{v_0^2}x^2</math></center>}} | + | <center><math>y = -\frac{1}{2} \frac{g}{v_0^2}x^2</math></center> |
| + | |||
| + | Bei den Gleichungen und der Parabel ist vorausgesetzt, dass der Koordinatenursprung des xy-Koordinatensystems im Abwurfpunkt ist.}} | ||
| + | |||
| + | {{Aufgaben-blau|2|2=Wie weit fliegt das Schwein? | ||
| + | |||
| + | <center>{{#ev:youtube |waWyKSICaQ4|350}}</center> }} | ||
| + | |||
| + | |||
| + | Beispielaufgabe: | ||
| + | <center>{{#ev:youtube |yCYZqRn3AVI|350}}</center> | ||
Version vom 2. März 2021, 14:06 Uhr
|
Merke:
Der waagrechte Wurf ist eine zweidimensionale Bewegung und setzt sich als Überlagerung
zusammen. |
Bei einem waagrechter Wurf wirft man einen Körper waagrecht mit einer Anfangsgeschwindigkeit los. Er fliegt dann geradlinigen in x-Richtung mit konstanter Geschwindigkeit weiter, gleichzeitig wirkt auf ihn seine Gewichtskraft in y-Richtung. Von dieser wird er mit konstanter Beschleunigung nach unten beschleunigt (freier Fall).
Beispielaufgabe:

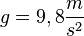 nach unten
nach unten