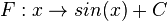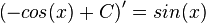M11 Ableitung der trigonometrischen Funktionen: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „__NOCACHE__ =Die Ableitung der Sinusfunktion= In dem folgenden Applet wird zu jedem Punkt P auf dem Graph der Sinusfunktion <math>f:x \to sin(x)</math> über …“) |
(→Die Ableitung der Sinusfunktion) |
||
| Zeile 6: | Zeile 6: | ||
{{Merksatz|MERK=Die Ableitung der Sinusfunktion ist die Kosinusfunktion. Es ist (sin x)' = cos x . }} | {{Merksatz|MERK=Die Ableitung der Sinusfunktion ist die Kosinusfunktion. Es ist (sin x)' = cos x . }} | ||
| + | |||
| + | Im Buch ist auf S. 137 unter 2. die Herleitung über die Definition der Ableitung nachzusehen | ||
=Die Ableitung der Kosinusfunktion= | =Die Ableitung der Kosinusfunktion= | ||
Version vom 4. März 2021, 11:17 Uhr
Inhaltsverzeichnis |
Die Ableitung der Sinusfunktion
In dem folgenden Applet wird zu jedem Punkt P auf dem Graph der Sinusfunktion 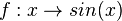 über der x-Koordinate von P die Steigung der Tangente aufgetragen. Bewegt man P auf dem Graphen, dann wird die Spur von A angezeigt.
über der x-Koordinate von P die Steigung der Tangente aufgetragen. Bewegt man P auf dem Graphen, dann wird die Spur von A angezeigt.
|
Merke:
Die Ableitung der Sinusfunktion ist die Kosinusfunktion. Es ist (sin x)' = cos x . |
Im Buch ist auf S. 137 unter 2. die Herleitung über die Definition der Ableitung nachzusehen
Die Ableitung der Kosinusfunktion
|
Merke:
Die Ableitung der Kosinusfunktion ist die negative Sinusfunktion. Es ist (cos x)' = - sin x . |
Man erhält die Ableitung der Kosinusfunktion auch mit Hilfe der Kettenregel. Es ist 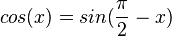 und
und 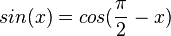 . Damit ist die Ableitung
. Damit ist die Ableitung 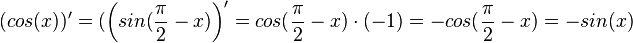
Die Ableitung der Tangensfunktion
Man weiß 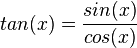 . Mit der Quotientenregel kann man
. Mit der Quotientenregel kann man 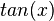 ableiten. Es ist
ableiten. Es ist 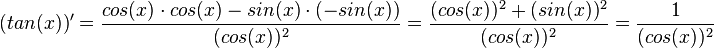
|
Merke:
Die Ableitung der Tangensfunktion ist |
Stammfunktionen
|
Merke:
Die Menge aller Stammfunktionen F der
|
Die Stammfunktionen weist man nach, indem man sie ableitet:
-
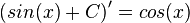 .
.

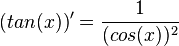 .
.
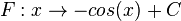
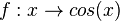 ist
ist