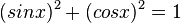M11 Ableitung der trigonometrischen Funktionen: Unterschied zwischen den Versionen
(→Aufgaben) |
|||
| Zeile 132: | Zeile 132: | ||
e) y' = <math>\frac{\pi}{3}\cdot cos(\frac{\pi}{6}x)</math> = 0 für <math>\frac{\pi}{6}x= \frac{\pi}{2}; \frac{3\pi}{2}</math> ergibt x = 3 oder x = 9<br> | e) y' = <math>\frac{\pi}{3}\cdot cos(\frac{\pi}{6}x)</math> = 0 für <math>\frac{\pi}{6}x= \frac{\pi}{2}; \frac{3\pi}{2}</math> ergibt x = 3 oder x = 9<br> | ||
f) y' <math>\frac{16}{\pi}sin(\frac{4}{\pi}x)</math> = 0 für <math>\frac{4}{\pi}x = 0; \pi; 2\pi</math> ergibt x = 0 }} | f) y' <math>\frac{16}{\pi}sin(\frac{4}{\pi}x)</math> = 0 für <math>\frac{4}{\pi}x = 0; \pi; 2\pi</math> ergibt x = 0 }} | ||
| − | <ggb_applet height="700" width=" | + | <ggb_applet height="700" width="1000" |
filename="134-2.ggb" /> | filename="134-2.ggb" /> | ||
| + | |||
| + | {{Aufgaben-blau|5|2=Buch S. 135 / 6 }} | ||
| + | |||
| + | {{Lösung versteckt|1=f(x) = 1 + sin(kx)<br> | ||
| + | a) Für k = 2 ist f(x) = 1 + sin(2x)<br> | ||
| + | Die Achsenpunkte erhält man für f(0) = 1, also auf der y-Achse (0;1) und auf der x-Achse sin(2x)=-1, also <math>2x = -\frac{\pi}{2};\frac{3\pi}{2}</math>, also <math>x = -\frac{\pi}{4}</math> und <math>x = \frac{3\pi}{4}</math>.<br> | ||
| + | Die Extremwerte erhält man durch Nullsetzen der Ableitungsfunktion f'. Es ist f'(x) = 2·cos(2x). Es ist 2·cos(2x) = 0, also cos(2x) = 0 für <math> x =- \frac{3\pi}{4}</math>, <math> x =- \frac{\pi}{4}</math>, <math>x = \frac{\pi}{4}</math> und <math> x = \frac{3\pi}{4}</math><br> | ||
| + | [[Datei:135-6a.jpg]] | ||
| + | |||
| + | b) f'(x) = k·cos(kx)<br> | ||
| + | Tangente in A(0;1): Steigung m = f'(0) = k<sup>*</sup>, y-Abschnitt t = 1, also y = k<sup>*</sup>·x + 1.<br> | ||
| + | Tangente in B(<math>\frac{\pi}{k^*}</math>;1) : m = f'(<math>\frac{\pi}{k^*}</math>)=<math>k^*\cdot cos(\pi)=-k^*</math>. <br> | ||
| + | t erhält man mit f((<math>\frac{\pi}{k^*}</math>)=1 aus der Gleichung 1 = <math>-k^* \cdot \frac{\pi}{k^*} +t</math> zu <math>t = 1-\pi</math>. Also ist die Gleichung der Tangente y = -k<sup>*</sup>x + 1 - <math>\pi</math>. <br> | ||
| + | Zwei Geraden stehen senkrecht zueinander, wenn das Produkt ihrer Steigungen -1 ist. | ||
| + | Also muss k<sup>*</sup>·(-k<sup>*</sup>) = -(k<sup>*</sup>)<sup>2</sup> = - 1 sein. Dies ist für k<sup>*</sup> = -1 oder k<sup>* = 1 </sup> erfüllt. Da k<sup>*</sup> positiv ist, erhält man als einzige Lösung k<sup>*</sup> = 1. | ||
| + | <center>[[Datei:135-6b.jpg]]</center> | ||
| + | Der Schnittpunkt der beiden Tangenten y = x + 1 und y = -x + 1 - <math>\pi</math> ist S(<math>-\frac{\pi}{2};1-\frac{\pi}{2}</math>).<br> | ||
| + | Aus der Zeichnung kann man ablesen, dass das Dreieck die Grundseite g = <math>\pi</math> und die Höhe h = <math>\frac{\pi}{2}</math> hat, also ist der Flächeninhalt des Dreiecks <math>A = \frac{1}{2}\cdot \pi \cdot \frac{\pi}{2}=\frac{\pi^2}{4}</math>. }} | ||
Version vom 10. März 2021, 12:46 Uhr
Inhaltsverzeichnis |
Die Ableitung der Sinusfunktion
In dem folgenden Applet wird zu jedem Punkt P auf dem Graph der Sinusfunktion 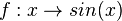 über der x-Koordinate von P die Steigung der Tangente aufgetragen. Bewegt man P auf dem Graphen, dann wird die Spur von A angezeigt.
über der x-Koordinate von P die Steigung der Tangente aufgetragen. Bewegt man P auf dem Graphen, dann wird die Spur von A angezeigt.
|
Merke:
Die Ableitung der Sinusfunktion ist die Kosinusfunktion. Es ist |
Im Buch ist auf S. 137 unter 2. die Herleitung über die Definition der Ableitung nachzusehen
Die Ableitung der Kosinusfunktion
|
Merke:
Die Ableitung der Kosinusfunktion ist die negative Sinusfunktion. Es ist |
Man erhält die Ableitung der Kosinusfunktion auch mit Hilfe der Kettenregel. Es ist 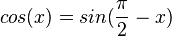 und
und 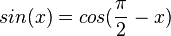 . Damit ist die Ableitung
. Damit ist die Ableitung 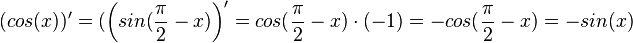
Die Ableitung der Tangensfunktion
Man weiß 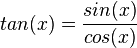 . Mit der Quotientenregel kann man
. Mit der Quotientenregel kann man 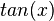 ableiten. Es ist
ableiten. Es ist 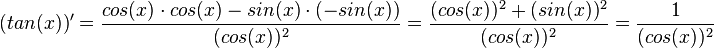
|
Merke:
Die Ableitung der Tangensfunktion ist |
Stammfunktionen
|
Merke:
Die Menge aller Stammfunktionen F der
|
Die Stammfunktionen weist man nach, indem man sie ableitet:
-
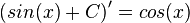 .
.
Aufgaben
30px Merke
Zur Wiederholung:
|
a) y' = - sin(x-3)
b) y' = cos(x2)· 2x = 2x cos(x2)
c) y' = cos(x) · cos(x) + sin(x) · (-cos(x)) = (cos(x))2 - (sin(x))2
d) y' = 2 sin(x) · cos(x) (nachdifferenzieren!)
e) y' = 2 cos(x) · ( - sin(x)) = - 2 sin(x)·cos(x)
f) y' = - a· sin(ax + b)
g) y' = 2x · sin(x) + x2 · cos(x)
h) Es ist 1 - (sin x)2 = (cos x)2. Daher ist y' = ((cos x)4)' = 4·(cos x)3· ( - sin x) = - 4 sin x · (cos x)3.
i) y' = 0
j) 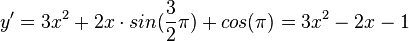
k) 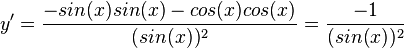
l) y' = 2[1- sin(2x)] · [ - 2 cos(2x)] oder y = (cos(2x))2 und y' = 2·cos(2x)·(-2sin(x))
m) y' = 0
n) 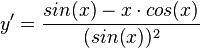
o) 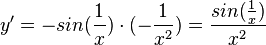
p) 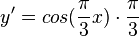
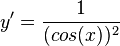
a)f(x) = sin(x), die Ableitungsfunktion f' ist f'(x) = cos(x)
f hat einen Extrempunkt in x0, wenn f#(x0 = 0 ist und ein VZW vorliegt.
(1) Im Intervall [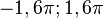 ] ist cos(x)= 0 für
] ist cos(x)= 0 für 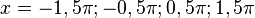
Bei 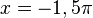 hat f' einen VZW +/-, also hat f ein Maximum.
hat f' einen VZW +/-, also hat f ein Maximum.
Bei 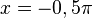 hat f' einen VZW -/+, also hat f ein Minimum.
hat f' einen VZW -/+, also hat f ein Minimum.
Bei 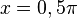 hat f' einen VZW +/-, also hat f ein Maximum.
hat f' einen VZW +/-, also hat f ein Maximum.
Bei 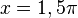 hat f' einen VZW -/+, also hat f ein Minimum.
hat f' einen VZW -/+, also hat f ein Minimum.
(2) f'(x) = cos(x) = 1 für 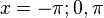
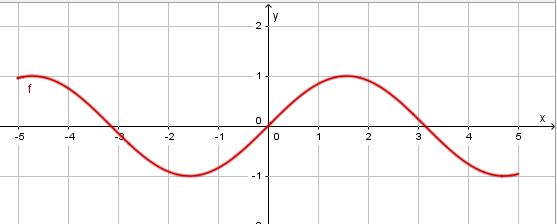
b) f(x) = cos(2x), D = ]-2;2[. die Ableitungsfunktion f' ist f'(x) = - 2·sin(2x)
(1) f'(x) = - 2·sin(2x) = 0 für 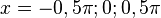
Bei 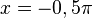 hat f' einen VZW -/+, also hat f ein Minimum.
hat f' einen VZW -/+, also hat f ein Minimum.
Bei 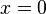 hat f' einen VZW +/-, also hat f ein Maximum.
hat f' einen VZW +/-, also hat f ein Maximum.
Bei 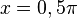 hat f' einen VZW -/+, also hat f ein Minimum.
hat f' einen VZW -/+, also hat f ein Minimum.
(2) f'(x) = - 2·sin(2x) = 1 für sin(2x) = - 0,5 und 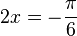 und
und 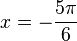 , also
, also 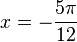 und
und 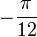 .
.
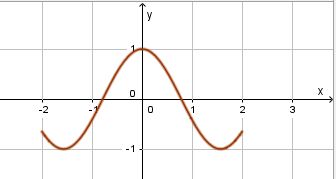
c) f(x) = tan(x) mit 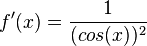
(1) In D ist f' stets positiv und nirgends 0, also hat f kein Extremum.
(2) f'(x) = 1 für 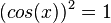 , also für x = 0.
, also für x = 0.
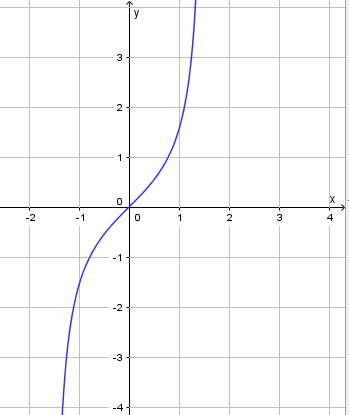
d) f(x) = 0,5 cos(2x + 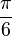 ) mit f'(x) = - sin(2x +
) mit f'(x) = - sin(2x + 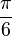 )
)
(1) f'(x) = - sin(2x + 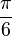 ) = 0, wenn
) = 0, wenn 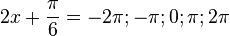 .
.
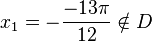
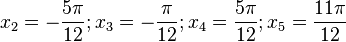
(2) f'(x) = - sin(2x + 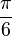 ) = 1 bzw. sin(2x +
) = 1 bzw. sin(2x + 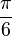 ) = - 1 für
) = - 1 für 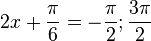
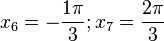
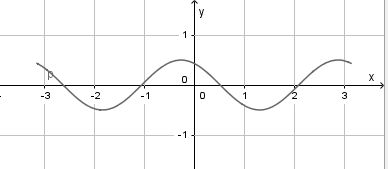
a) F(x) = -0,5·cos(2x) + C
b) F(x) =  ·sin(
·sin(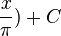
c) F(x) = 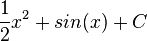
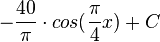
weitere Aufgaben
Zuerst wird immer das Grundintervall [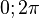 ] betrachtet und danach auf die angegebene Grundmenge übertragen.
] betrachtet und danach auf die angegebene Grundmenge übertragen.
a) y' = cos(x) = 0 für 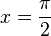 oder
oder 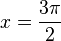
b) y' = 1 + sin(x) = 0 für sin(x) = -1, also 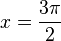 im Grundintervall und in G ist
im Grundintervall und in G ist 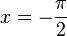 oder
oder 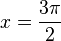
c) y' = -sin(2x) - 1 = 0 ergibt sin(2x) = -1 und 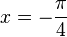 oder
oder 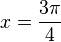
d) y' = 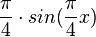 = 0 für
= 0 für 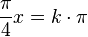 ergibt x = -4 oder x = 0 oder x = 4</math>
ergibt x = -4 oder x = 0 oder x = 4</math>
e) y' = 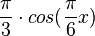 = 0 für
= 0 für 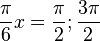 ergibt x = 3 oder x = 9
ergibt x = 3 oder x = 9
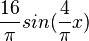 = 0 für
= 0 für 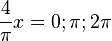 ergibt x = 0
ergibt x = 0
f(x) = 1 + sin(kx)
a) Für k = 2 ist f(x) = 1 + sin(2x)
Die Achsenpunkte erhält man für f(0) = 1, also auf der y-Achse (0;1) und auf der x-Achse sin(2x)=-1, also 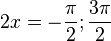 , also
, also 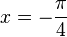 und
und 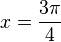 .
.
Die Extremwerte erhält man durch Nullsetzen der Ableitungsfunktion f'. Es ist f'(x) = 2·cos(2x). Es ist 2·cos(2x) = 0, also cos(2x) = 0 für 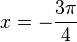 ,
, 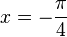 ,
, 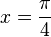 und
und 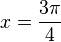
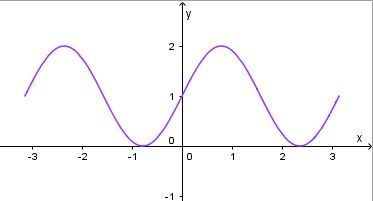
b) f'(x) = k·cos(kx)
Tangente in A(0;1): Steigung m = f'(0) = k*, y-Abschnitt t = 1, also y = k*·x + 1.
Tangente in B(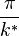 ;1) : m = f'(
;1) : m = f'(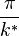 )=
)=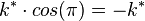 .
.
t erhält man mit f((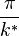 )=1 aus der Gleichung 1 =
)=1 aus der Gleichung 1 = 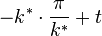 zu
zu 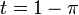 . Also ist die Gleichung der Tangente y = -k*x + 1 -
. Also ist die Gleichung der Tangente y = -k*x + 1 -  .
.
Zwei Geraden stehen senkrecht zueinander, wenn das Produkt ihrer Steigungen -1 ist.
Also muss k*·(-k*) = -(k*)2 = - 1 sein. Dies ist für k* = -1 oder k* = 1 erfüllt. Da k* positiv ist, erhält man als einzige Lösung k* = 1.
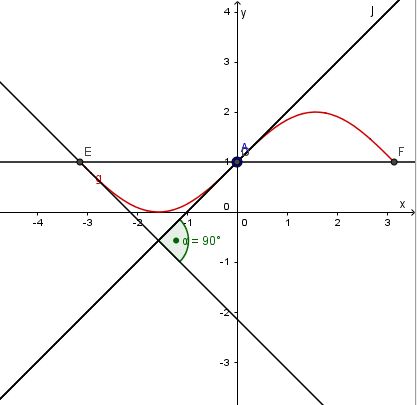
Der Schnittpunkt der beiden Tangenten y = x + 1 und y = -x + 1 -  ist S(
ist S(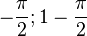 ).
).
 und die Höhe h =
und die Höhe h = 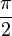 hat, also ist der Flächeninhalt des Dreiecks
hat, also ist der Flächeninhalt des Dreiecks 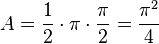 .
.
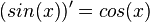 .
.
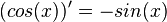 .
.
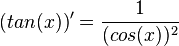 .
.
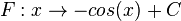
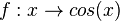 ist
ist 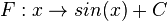
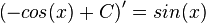
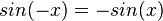 und
und