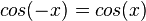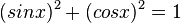M11 Ableitung der trigonometrischen Funktionen: Unterschied zwischen den Versionen
(→weitere Aufgaben) |
(→weitere Aufgaben) |
||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 168: | Zeile 168: | ||
{{Aufgaben-blau|7|2=Buch S. 135 / 8 }} | {{Aufgaben-blau|7|2=Buch S. 135 / 8 }} | ||
| + | |||
| + | {{Lösung versteckt|1=a) siehe Applet unten<br> | ||
| + | |||
| + | b)F'(x) = 2 + cos(x) = f(x)<br> | ||
| + | G'(x) = <math>\frac{1}{2} -\frac{1}{2}\left ( cos(x)\cdot cos(x) - sin(x)\cdot sin(x) \right) =\frac{1}{2} -\frac{1}{2}\left ( (cos(x))^2 - (sin(x))^2 \right) =\frac{1}{2} -\frac{1}{2}\left ( 1 - (sin(x))^2 - (sin(x))^2 \right) = </math><br> | ||
| + | <math>\frac{1}{2} -\frac{1}{2}\left (1-2(sin(x))^2 \right)= \frac{1}{2} -\frac{1}{2} + (sin(x))^2 = g(x)</math> | ||
| + | |||
| + | c) Laut Konstuktion ist d(a) = y<sub>P</sub> - y<sub>Q </sub> = f(a) - g(a).<br> | ||
| + | d ist minimal in a<sup>*</sup>, wenn d' für a = a<sup>*</sup> eine Nullstelle mit VZW -/+ hat.<br> | ||
| + | d'(a) = (2 + cos(a) -(sin(a))<sup>2</sup>)' = -sin(a) - 2sin(a)cos(a) = -sin(a)[1+2cos(a)]<br> | ||
| + | -sin(a)[1+2cos(a)] = 0 für sin(a) = 0, also a = 0 oder a = <math>\pi</math> oder<br> | ||
| + | 1+2cos(a) = 0, also <math>cos(a)=-\frac{1}{2}</math> und <math>a = \frac{2\pi}{3}</math><br> | ||
| + | Für a <math>\in</math> [0;<math>\pi</math>] ist -sin(a) stets negativ, 1 + 2cos(a) ist für 0 ≤ x < <math>\frac{2\pi}{3}</math> positiv(, also d' ist insgesamt dort negativ) und für <math>\frac{2\pi}{3}</math> < a < <math>\pi</math> negativ(, also d# ist dort insgesamt positiv). Also hat d' bei a = <math>\frac{2\pi}{3}</math> einen VZW -/+ und d hat dort ein Minimum. <br> | ||
| + | Es ist <math>d(\frac{2\pi}{3})= 2 -\frac{1}{2} - \frac{3}{4}=0,75</math><br> | ||
| + | Aus der Zeichnung sieht man, dass d für a = 0 oder a = <math>\pi</math> kein Minimum hat. | ||
| + | |||
| + | Die Steigung der Tangente in P ist f'(<math>\frac{2\pi}{3}</math>) = -sin(<math>\frac{2\pi}{3}</math>) = <math>-\frac{\sqrt 3}{2}</math>.<br> | ||
| + | Die Steigung der Tangente in Q ist g'(x) = 2sin(<math>\frac{2\pi}{3}</math>)cos(<math>\frac{2\pi}{3}</math>)=<math>2\cdot \frac{\sqrt 3}{2}\cdot (-\frac{1}{2})=-\frac{\sqrt 3}{2}</math>. <br> | ||
| + | Also sind die beiden Tangenten dort parallel. }} | ||
| + | |||
| + | |||
| + | <ggb_applet height="500" width="700" | ||
| + | filename="135-8.ggb" /> | ||
| + | |||
| + | {{Aufgaben-blau|8|2=Buch S. 136 / 10 }} | ||
Aktuelle Version vom 10. März 2021, 17:18 Uhr
Inhaltsverzeichnis |
Die Ableitung der Sinusfunktion
In dem folgenden Applet wird zu jedem Punkt P auf dem Graph der Sinusfunktion 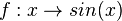 über der x-Koordinate von P die Steigung der Tangente aufgetragen. Bewegt man P auf dem Graphen, dann wird die Spur von A angezeigt.
über der x-Koordinate von P die Steigung der Tangente aufgetragen. Bewegt man P auf dem Graphen, dann wird die Spur von A angezeigt.
|
Merke:
Die Ableitung der Sinusfunktion ist die Kosinusfunktion. Es ist |
Im Buch ist auf S. 137 unter 2. die Herleitung über die Definition der Ableitung nachzusehen
Die Ableitung der Kosinusfunktion
|
Merke:
Die Ableitung der Kosinusfunktion ist die negative Sinusfunktion. Es ist |
Man erhält die Ableitung der Kosinusfunktion auch mit Hilfe der Kettenregel. Es ist 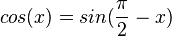 und
und 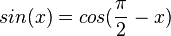 . Damit ist die Ableitung
. Damit ist die Ableitung 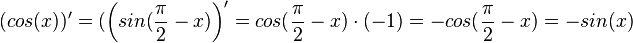
Die Ableitung der Tangensfunktion
Man weiß 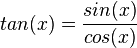 . Mit der Quotientenregel kann man
. Mit der Quotientenregel kann man 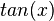 ableiten. Es ist
ableiten. Es ist 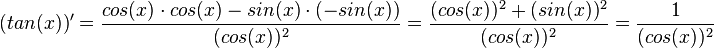
|
Merke:
Die Ableitung der Tangensfunktion ist |
Stammfunktionen
|
Merke:
Die Menge aller Stammfunktionen F der
|
Die Stammfunktionen weist man nach, indem man sie ableitet:
-
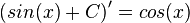 .
.
Aufgaben
30px Merke
Zur Wiederholung:
|
a) y' = - sin(x-3)
b) y' = cos(x2)· 2x = 2x cos(x2)
c) y' = cos(x) · cos(x) + sin(x) · (-cos(x)) = (cos(x))2 - (sin(x))2
d) y' = 2 sin(x) · cos(x) (nachdifferenzieren!)
e) y' = 2 cos(x) · ( - sin(x)) = - 2 sin(x)·cos(x)
f) y' = - a· sin(ax + b)
g) y' = 2x · sin(x) + x2 · cos(x)
h) Es ist 1 - (sin x)2 = (cos x)2. Daher ist y' = ((cos x)4)' = 4·(cos x)3· ( - sin x) = - 4 sin x · (cos x)3.
i) y' = 0
j) 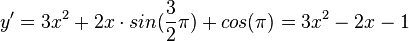
k) 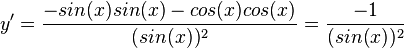
l) y' = 2[1- sin(2x)] · [ - 2 cos(2x)] oder y = (cos(2x))2 und y' = 2·cos(2x)·(-2sin(x))
m) y' = 0
n) 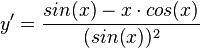
o) 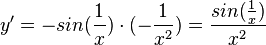
p) 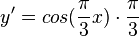
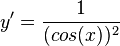
a)f(x) = sin(x), die Ableitungsfunktion f' ist f'(x) = cos(x)
f hat einen Extrempunkt in x0, wenn f#(x0 = 0 ist und ein VZW vorliegt.
(1) Im Intervall [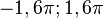 ] ist cos(x)= 0 für
] ist cos(x)= 0 für 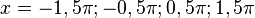
Bei 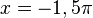 hat f' einen VZW +/-, also hat f ein Maximum.
hat f' einen VZW +/-, also hat f ein Maximum.
Bei 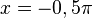 hat f' einen VZW -/+, also hat f ein Minimum.
hat f' einen VZW -/+, also hat f ein Minimum.
Bei 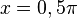 hat f' einen VZW +/-, also hat f ein Maximum.
hat f' einen VZW +/-, also hat f ein Maximum.
Bei 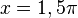 hat f' einen VZW -/+, also hat f ein Minimum.
hat f' einen VZW -/+, also hat f ein Minimum.
(2) f'(x) = cos(x) = 1 für 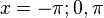
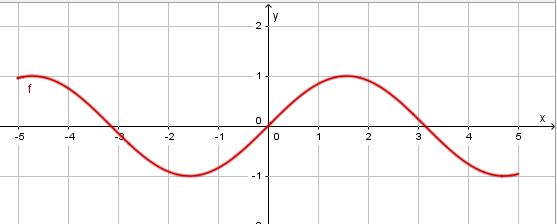
b) f(x) = cos(2x), D = ]-2;2[. die Ableitungsfunktion f' ist f'(x) = - 2·sin(2x)
(1) f'(x) = - 2·sin(2x) = 0 für 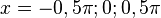
Bei 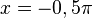 hat f' einen VZW -/+, also hat f ein Minimum.
hat f' einen VZW -/+, also hat f ein Minimum.
Bei 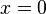 hat f' einen VZW +/-, also hat f ein Maximum.
hat f' einen VZW +/-, also hat f ein Maximum.
Bei 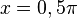 hat f' einen VZW -/+, also hat f ein Minimum.
hat f' einen VZW -/+, also hat f ein Minimum.
(2) f'(x) = - 2·sin(2x) = 1 für sin(2x) = - 0,5 und 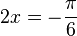 und
und 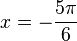 , also
, also 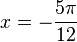 und
und 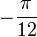 .
.
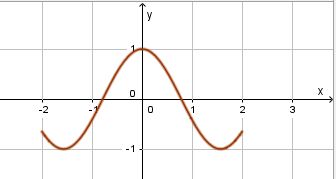
c) f(x) = tan(x) mit 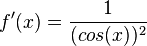
(1) In D ist f' stets positiv und nirgends 0, also hat f kein Extremum.
(2) f'(x) = 1 für 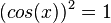 , also für x = 0.
, also für x = 0.
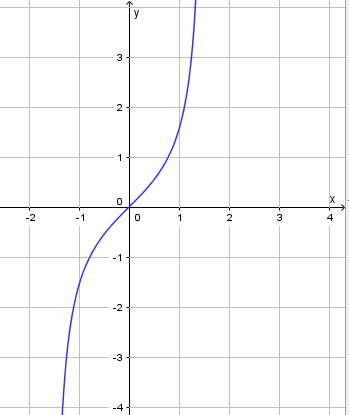
d) f(x) = 0,5 cos(2x + 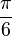 ) mit f'(x) = - sin(2x +
) mit f'(x) = - sin(2x + 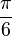 )
)
(1) f'(x) = - sin(2x + 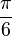 ) = 0, wenn
) = 0, wenn 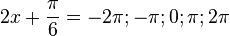 .
.
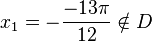
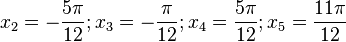
(2) f'(x) = - sin(2x + 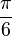 ) = 1 bzw. sin(2x +
) = 1 bzw. sin(2x + 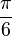 ) = - 1 für
) = - 1 für 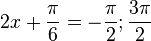
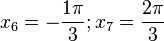
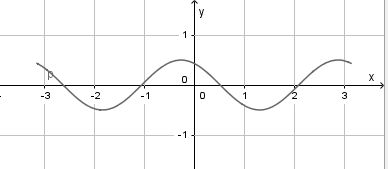
a) F(x) = -0,5·cos(2x) + C
b) F(x) =  ·sin(
·sin(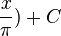
c) F(x) = 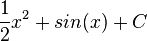
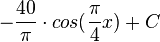
weitere Aufgaben
Zuerst wird immer das Grundintervall [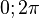 ] betrachtet und danach auf die angegebene Grundmenge übertragen.
] betrachtet und danach auf die angegebene Grundmenge übertragen.
a) y' = cos(x) = 0 für 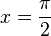 oder
oder 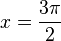
b) y' = 1 + sin(x) = 0 für sin(x) = -1, also 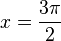 im Grundintervall und in G ist
im Grundintervall und in G ist 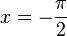 oder
oder 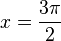
c) y' = -sin(2x) - 1 = 0 ergibt sin(2x) = -1 und 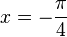 oder
oder 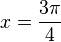
d) y' = 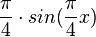 = 0 für
= 0 für 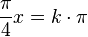 ergibt x = -4 oder x = 0 oder x = 4</math>
ergibt x = -4 oder x = 0 oder x = 4</math>
e) y' = 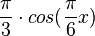 = 0 für
= 0 für 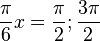 ergibt x = 3 oder x = 9
ergibt x = 3 oder x = 9
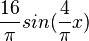 = 0 für
= 0 für 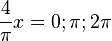 ergibt x = 0
ergibt x = 0
f(x) = 1 + sin(kx)
a) Für k = 2 ist f(x) = 1 + sin(2x)
Die Achsenpunkte erhält man für f(0) = 1, also auf der y-Achse (0;1) und auf der x-Achse sin(2x)=-1, also 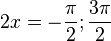 , also
, also 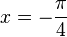 und
und 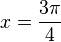 .
.
Die Extremwerte erhält man durch Nullsetzen der Ableitungsfunktion f'. Es ist f'(x) = 2·cos(2x). Es ist 2·cos(2x) = 0, also cos(2x) = 0 für 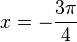 ,
, 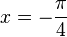 ,
, 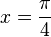 und
und 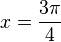
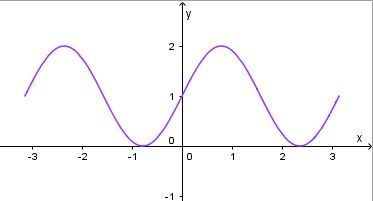
b) f'(x) = k·cos(kx)
Tangente in A(0;1): Steigung m = f'(0) = k*, y-Abschnitt t = 1, also y = k*·x + 1.
Tangente in B(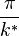 ;1) : m = f'(
;1) : m = f'(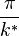 )=
)=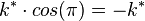 .
.
t erhält man mit f((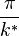 )=1 aus der Gleichung 1 =
)=1 aus der Gleichung 1 = 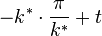 zu
zu 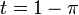 . Also ist die Gleichung der Tangente y = -k*x + 1 -
. Also ist die Gleichung der Tangente y = -k*x + 1 -  .
.
Zwei Geraden stehen senkrecht zueinander, wenn das Produkt ihrer Steigungen -1 ist.
Also muss k*·(-k*) = -(k*)2 = - 1 sein. Dies ist für k* = -1 oder k* = 1 erfüllt. Da k* positiv ist, erhält man als einzige Lösung k* = 1.
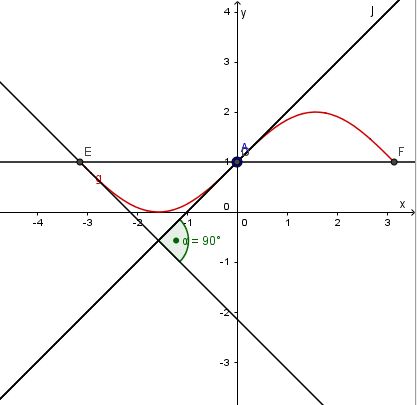
Der Schnittpunkt der beiden Tangenten y = x + 1 und y = -x + 1 -  ist S(
ist S(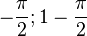 ).
).
 und die Höhe h =
und die Höhe h = 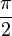 hat, also ist der Flächeninhalt des Dreiecks
hat, also ist der Flächeninhalt des Dreiecks 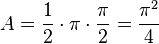 .
.
a) 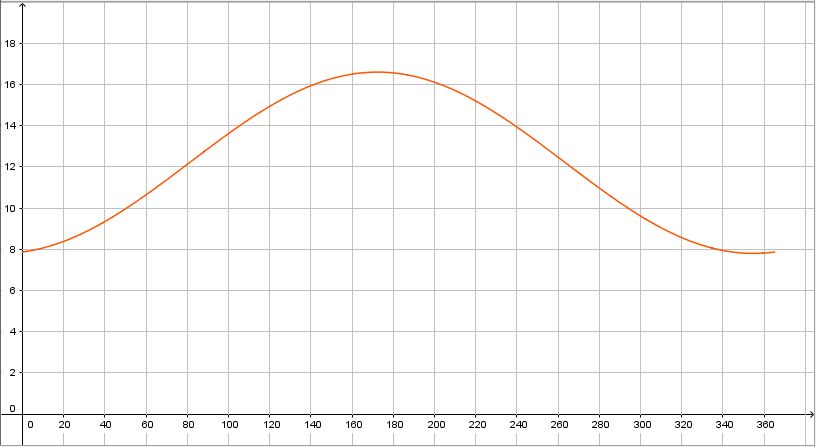
b)Größte Tageslänge 12,2 + 4,4 = 16,6 (h)
kürzeste Tageslänge 12,2 - 4,4 = 7,8 (h)
Das Datum erhält man durch Bestimmung des Extremwerte. 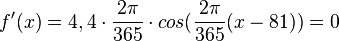 .
.
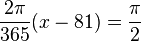 oder
oder 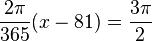 .
.
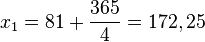 und
und 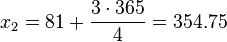
Auf dieser Seite kann man nachsehen, welches Datum diese Tage haben. Der 172. Tag im Jahr ist der 21. Juni, der 355. Tag des Jahres ist der 21. Dezember.
c) Der 21. März ist der 80. Tag im Jahr und die Tageslänge ist f(80)=12,12 (h),
der 21. Juni ist der 172. Tag im Jahr und die Tageslänge ist 16,6 (h),
der 23. September ist der 266.Tag im Jahr und die Tageslänge ist 12,01 (h),
a) siehe Applet unten
b)F'(x) = 2 + cos(x) = f(x)
G'(x) = 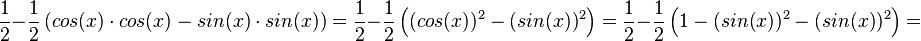
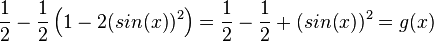
c) Laut Konstuktion ist d(a) = yP - yQ = f(a) - g(a).
d ist minimal in a*, wenn d' für a = a* eine Nullstelle mit VZW -/+ hat.
d'(a) = (2 + cos(a) -(sin(a))2)' = -sin(a) - 2sin(a)cos(a) = -sin(a)[1+2cos(a)]
-sin(a)[1+2cos(a)] = 0 für sin(a) = 0, also a = 0 oder a =  oder
oder
1+2cos(a) = 0, also 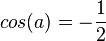 und
und 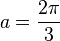
Für a 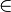 [0;
[0; ] ist -sin(a) stets negativ, 1 + 2cos(a) ist für 0 ≤ x <
] ist -sin(a) stets negativ, 1 + 2cos(a) ist für 0 ≤ x < 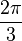 positiv(, also d' ist insgesamt dort negativ) und für
positiv(, also d' ist insgesamt dort negativ) und für 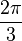 < a <
< a <  negativ(, also d# ist dort insgesamt positiv). Also hat d' bei a =
negativ(, also d# ist dort insgesamt positiv). Also hat d' bei a = 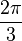 einen VZW -/+ und d hat dort ein Minimum.
einen VZW -/+ und d hat dort ein Minimum.
Es ist 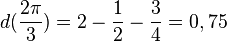
Aus der Zeichnung sieht man, dass d für a = 0 oder a =  kein Minimum hat.
kein Minimum hat.
Die Steigung der Tangente in P ist f'(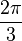 ) = -sin(
) = -sin(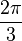 ) =
) = 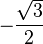 .
.
Die Steigung der Tangente in Q ist g'(x) = 2sin(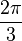 )cos(
)cos(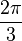 )=
)=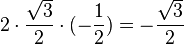 .
.

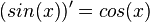 .
.
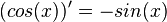 .
.
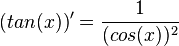 .
.
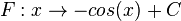
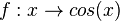 ist
ist 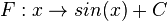
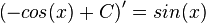
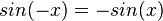 und
und