M9 Die Wurzelfunktion: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „Die Quadratfunktion <math>f: x \to x^2</math> mit D = R wird jeder Zahl x ihre Quadratzahl x<sup>2</sup> zugeordnet. Ihr Graph ist die Normalparabel. <center>…“) |
|||
| Zeile 1: | Zeile 1: | ||
| + | __NOCACHE__ | ||
Die Quadratfunktion <math>f: x \to x^2</math> mit D = R wird jeder Zahl x ihre Quadratzahl x<sup>2</sup> zugeordnet. Ihr Graph ist die Normalparabel. | Die Quadratfunktion <math>f: x \to x^2</math> mit D = R wird jeder Zahl x ihre Quadratzahl x<sup>2</sup> zugeordnet. Ihr Graph ist die Normalparabel. | ||
<center>[[Datei:X^2.jpg|350px]]</center> | <center>[[Datei:X^2.jpg|350px]]</center> | ||
| Zeile 22: | Zeile 23: | ||
{{Merksatz|MERK=Die Wurzelfunktion <math>g:x\to \sqrt x</math> mit D<sub>g</sub> = R<math>^+_0</math> ist die Umkehrfunktion zur Quadratfunktion <math>f:x \to x^2</math> mit D<sub>f</sub> = R<math>^+_0</math> }} | {{Merksatz|MERK=Die Wurzelfunktion <math>g:x\to \sqrt x</math> mit D<sub>g</sub> = R<math>^+_0</math> ist die Umkehrfunktion zur Quadratfunktion <math>f:x \to x^2</math> mit D<sub>f</sub> = R<math>^+_0</math> }} | ||
| + | |||
| + | |||
| + | =Ausblicke= | ||
| + | |||
| + | Die Wurzelfunktion kann man auch verschieben und spiegeln. | ||
| + | <center><ggb_applet height="400" width="600" | ||
| + | filename="Wurzelfunktion_bd.ggb" /></center> | ||
| + | |||
| + | <div class="zuordnungs-quiz"> | ||
| + | |||
| + | {| | ||
| + | | a || Spiegelung an der x-Achse | ||
| + | |- | ||
| + | | b || Verschiebung in x-Richtung | ||
| + | |- | ||
| + | | d || Verschiebung in y-Richtung | ||
| + | |} | ||
| + | |||
| + | </div> | ||
Mehr zur Bildung der Umkehrfunktion findest du auf [[Die_Umkehrfunktion|diesen Seiten.]] | Mehr zur Bildung der Umkehrfunktion findest du auf [[Die_Umkehrfunktion|diesen Seiten.]] | ||
Version vom 24. März 2021, 07:13 Uhr
Die Quadratfunktion 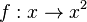 mit D = R wird jeder Zahl x ihre Quadratzahl x2 zugeordnet. Ihr Graph ist die Normalparabel.
mit D = R wird jeder Zahl x ihre Quadratzahl x2 zugeordnet. Ihr Graph ist die Normalparabel.
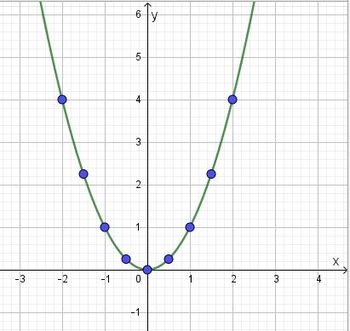
Dies kann man auch umgekehrt machen. Man ordnet jeder Zahl x ihre Quadratwurzel 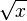 . Dies führt zu einer neuen Funktion. Weil im Funktionsterm eine Wurzel vorkommt, heißt diese Funktion
. Dies führt zu einer neuen Funktion. Weil im Funktionsterm eine Wurzel vorkommt, heißt diese Funktion 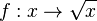 mit D = R
mit D = R Wurzelfunktion.
Wurzelfunktion.
|
Merke:
Die Funktion |
| Als Wertetabelle erhält man | und der dazugehörige Graph |
| |
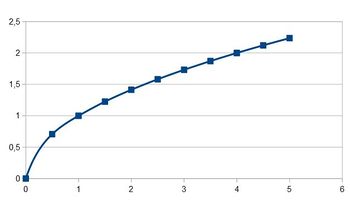
|
Zeichnet man die Parabel der Quadratfunktion auch nur für nicht negative x-Werte und ergänzt in diesem Diagramm den Graph der Wurzelfunktion und die Gerade y = x, dann erhält man dieses Bild:
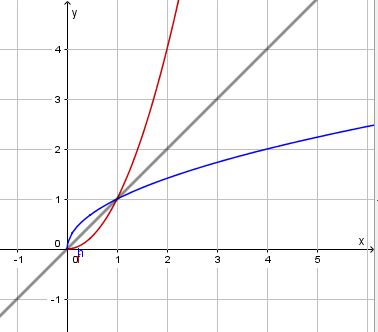
30px Merke
Bezüglich der Geraden y = x sind die Graphen der Quadratfunktion und der Wurzelfunktion symmetrisch. |
Wenn man eine Funktion und ihre Umkehrfunktion nacheinander ausführt, dann erhält man wieder das ursprüngliche x. Quadriert man x zuerst, dann hat man x2 und wenn man aus x2 wieder die Wurzel zieht, erhält man wieder x. Man kann auch zuerst aus x die Wurzel ziehen und erhält 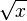 und wenn man
und wenn man 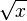 quadriert erhält man auch wieder x.
quadriert erhält man auch wieder x.
|
Merke:
Die Wurzelfunktion |
Ausblicke
Die Wurzelfunktion kann man auch verschieben und spiegeln.
| a | Spiegelung an der x-Achse |
| b | Verschiebung in x-Richtung |
| d | Verschiebung in y-Richtung |
Mehr zur Bildung der Umkehrfunktion findest du auf diesen Seiten.

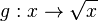 mit Dg = R
mit Dg = R
