M9 Potenzen mit rationalen Exponenten: Unterschied zwischen den Versionen
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 135: | Zeile 135: | ||
c) <math>0,2^{\frac{1}{3}}=5^{-\frac{1}{3}}</math> - Die Basis soll eine natürliche Zahl sein!<br> | c) <math>0,2^{\frac{1}{3}}=5^{-\frac{1}{3}}</math> - Die Basis soll eine natürliche Zahl sein!<br> | ||
d) <math>\left ( \frac{1}{40} \right)^{\frac{1}{12}}=40^{-\frac{1}{12}}</math><br> | d) <math>\left ( \frac{1}{40} \right)^{\frac{1}{12}}=40^{-\frac{1}{12}}</math><br> | ||
| + | Hier kann man das Ergebnis noch teilweise radizieren. Es ist <math>40 = 2^3 \cdot 5</math>, also <math>40^{-\frac{1}{12}}=(2^3 \cdot 5)^{-\frac{1}{12}}=2^{-\frac{3}{12}}\cdot 5^{-\frac{1}{12}}=2^{-\frac{1}{4}}\cdot 5^{-\frac{1}{12}}</math><br> | ||
e) <math>2^{\frac{5}{4}}</math><br> | e) <math>2^{\frac{5}{4}}</math><br> | ||
f) <math>3^{\frac{1}{2}}=3^{0,5}</math> }} | f) <math>3^{\frac{1}{2}}=3^{0,5}</math> }} | ||
| Zeile 201: | Zeile 202: | ||
Bei d) führt die Frage nach dem Schnittpunkt auf die Gleichung x<sup>3</sup> = 2, die man in b) schon gelöst hat. | Bei d) führt die Frage nach dem Schnittpunkt auf die Gleichung x<sup>3</sup> = 2, die man in b) schon gelöst hat. | ||
| − | Allgemein kann man die Problemstellung lösen. Der "alte Altar" hat das Volumen V = | + | Allgemein kann man die Problemstellung lösen. Der "alte Altar" hat das Volumen V = a<sup>3</sup>. Der neue Altar mit Seitenlänge b soll doppeltes Volumen haben, also V = b<sup>3</sup> = 2 · a<sup>3</sup>. Dies führt zur Gleichung b<sup>3 </sup> = 2 · a<sup>3</sup> und zur Lösung <math>b = \sqrt [3] {2} \cdot a</math>. |
117 /11<br> | 117 /11<br> | ||
Aktuelle Version vom 24. März 2021, 17:53 Uhr
|
Merke:
Für die allgemeine Wurzel ![\sqrt[n]{a}=a^{\frac{1}{n}}](/images/math/e/c/8/ec88827417db352f94755f7f655c012e.png) Weiter ist Insbesondere ist |
Beispiele:
![27^{\frac{1}{3}} = \sqrt[3]{27} = 3](/images/math/6/e/8/6e8b5f8071aa6a25cb0f202b8ba28051.png)
![8^{\frac{2}{3}} = \sqrt[3]{8^2} = \sqrt [3]{64}=4](/images/math/a/9/9/a9981ffa899cb5fc81666a32ca3ae621.png)
![512^{\frac{1}{9}} = \sqrt[9]{512} = 2](/images/math/e/8/0/e804c035be7a66369ae590d14c7ec8c6.png)
![625^{\frac{1}{4}} = \sqrt[4]{625} = 5](/images/math/a/2/f/a2ff86b33bcc0725236122aa44d36741.png)
![625^{-\frac{1}{4}} = \sqrt[4]{625^{-1}} = \sqrt[4]{\frac{1}{625}}=\frac{1}{5}](/images/math/d/6/9/d694859f313981c26eba156aa47b7e05.png)
![256^{\frac{3}{8}} = \sqrt[8]{256^3} = \sqrt[8]{(2^8)^3}=\sqrt[8]{2^{24}}=\sqrt[8]{(2^3)^8}=2^3=8](/images/math/e/8/e/e8e7596fa7f078fbeb49e31978f6cb6e.png)
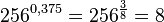
30px Merke
Für ![a^{\frac{m}{n}}=\sqrt[n]{a^m}](/images/math/4/3/e/43edac46411a2ae56ea7d55ac06fa113.png) oder oder ![a^{\frac{m}{n}}=(\sqrt [n]{a})^m](/images/math/b/e/e/beea25fd5ff600a78edbc3cf7ee38b6c.png) . . |
|
Sind r und s rationale Zahlen, dann schreibt es sich einfacher
|
Beispiele:
Vereinfache so weit als möglich:
![\sqrt 5 \cdot \sqrt [3]{5}=5^{\frac{1}{2}}\cdot 5^{\frac{1}{3}}=5^{\frac{1}{2}+\frac{1}{3}}=5^{\frac{5}{6}}=\sqrt[6]{5^5}\approx 3,82](/images/math/d/e/f/def72b8ad37822f3f0f409f2eb94a9a2.png)
![6^{\frac{1}{2}}: 6^{\frac{1}{3}}=6^{\frac{1}{2}-\frac{1}{3}}=6^{\frac{1}{6}}=\sqrt[6]{6}\approx 1,35](/images/math/c/3/e/c3e6ac2a5eb7707c7b969c3de5077bc2.png)
![4^{\frac{1}{3}}\cdot 2^{\frac{1}{3}}=8^{\frac{1}{3}}=\sqrt[3]{8}=2](/images/math/9/b/a/9ba85295a1248aea2b67f7af04c15dfb.png)
![28^{\frac{1}{3}}: 3,5^{\frac{1}{3}}=8^{\frac{1}{3}}=\sqrt[3]{8}=2](/images/math/e/c/e/eceb67224260995be9675f244f8d3d3a.png)
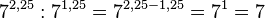
![\sqrt 5 \cdot \sqrt [3]{25}=5^{\frac{1}{2}}\cdot 5^{\frac{2}{3}}=5^{\frac{1}{2}+\frac{2}{3}}=5^{\frac{7}{6}}=\sqrt[6]{5^7}=5\cdot\sqrt[6]{5}\approx 6,54](/images/math/b/f/3/bf329728c7f8298f22059fb411fcf813.png)
Radiziere so weit als möglich (teilweises Radizieren)
![\sqrt [5]{3072} = \sqrt [5]{3\cdot 1024}=\sqrt [5]{3\cdot 4^5}=4\cdot \sqrt[5]{3}\approx4,98](/images/math/5/2/f/52f6585e40e962fb46cddf2c2af38e0c.png)
![\sqrt[6]{640}=\sqrt [6]{10\cdot 2^6}=2\sqrt [6]{10}\approx 2,94](/images/math/a/6/3/a639a18f0495d9f749a8bea4a38dd4ef.png)
30px Merke
Noch ein paar Tipps bevor es ans Rechnen geht! Wenn ein Minuszeichen im Exponenten steht, dann beachte, dass Bei der Einführung der rationalen Exponenten ist Am Beispiel
|
a) ) ![81^{\frac{1}{4}} = \sqrt [4]{3^4}=3](/images/math/4/2/c/42c469c31e1c832e114f5e468b21b0b6.png)
![216^{\frac{1}{3}}=\sqrt [3]{6^3}=6](/images/math/e/2/0/e20883bf76c8c130e328ce78511e3942.png)
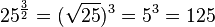
![32^{\frac{3}{5}}=(\sqrt[5]{2^5})^3=2^3=8](/images/math/c/b/8/cb800038fa4997b4530e2589dfde9907.png)
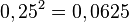
b) Es ist oft sinnvoll zuerst die Wurzel zu ziehen (Nenner) und dann zu Potenzieren (Zähler).
![10000^{-\frac{1}{4}}=\left ( \frac{1}{10000} \right )^{\frac{1}{4}}=\sqrt [4]{\frac{1}{10^4}}=\frac{1}{10}](/images/math/9/1/6/9161186f8280b741f29b4f4b2f4fed25.png)
![512^{\frac{2}{3}}=(\sqrt [3] {512}^2=8^2=64](/images/math/c/e/8/ce8fdb7b4cdda3e953c6a1ac3488b155.png)
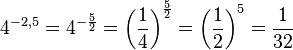
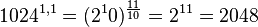
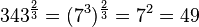
c) Auch hier zuerst (mit den Nenner) radizieren und dann (mit dem Zähler) potenzieren.
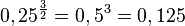
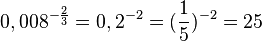
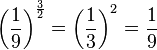
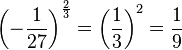
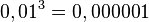
d) ![-\left ( \frac{27}{64}\right) ^{\frac{1}{3}}=- \sqrt[3]{\frac{27}{64}}=-\frac{3}{4}](/images/math/d/9/6/d96b6c2510ade835f212a16f4f00c5b6.png)
![\left ( \frac{27}{64}\right) ^{-\frac{1}{3}}=\left ( \frac{64}{27}\right) ^{\frac{1}{3}}=\sqrt [3]{\frac{64}{27}}=\frac{4}{3}](/images/math/e/e/e/eeeb042d3fee85233de74dd860578fbf.png)
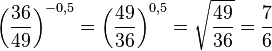
![- \left ( \frac{81}{256}\right) ^{-0,25}= - \left ( \frac{256}{81}\right) ^{\frac{1}{4}}=-\sqrt[4]{\frac{256}{81}}=-\frac{4}{3}](/images/math/9/e/b/9ebb19c0c0a90f95dcf75ccddfde9ded.png)
![-64^{\frac{1}{3}}=-\sqrt[3]{64}=-4](/images/math/e/9/5/e95b6edc78a145651183b7f3bf2f9eb9.png)
![\left (- \frac{16}{625} \right )^{0,75}=\left ( -\frac{16}{625} \right )^{\frac{3}{4}}=\sqrt[4]{ -\frac{16}{625}}](/images/math/f/5/d/f5d811cf457624153ff7cd2f0a1a64b6.png) kann man nicht vereinfachen, da bei einer 4. Wurzel (geraden Wurzel) der Radikand nicht negativ sein darf!
kann man nicht vereinfachen, da bei einer 4. Wurzel (geraden Wurzel) der Radikand nicht negativ sein darf!
116/2 a) ![\sqrt 6; \sqrt[3]{12}; \sqrt [4]{8}; \sqrt [3]{0,0625};\sqrt [5] {5}; \sqrt 2; \sqrt {0,5}; 0,0625](/images/math/5/9/3/593a96a3df6088fdfab5ba7cf73b2aff.png)
b) 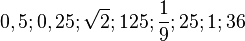
c) ![\sqrt [3] {a}; \sqrt [4] {b^3};\sqrt [4]{\frac{1}{c^3}}; \sqrt [5]{\frac{1}{d^2}}; \sqrt[5]{e^4}; \sqrt[5]{\frac{1}{f^{13}}}; \sqrt [4]{g}; \sqrt [5]{h^{36}}](/images/math/c/f/5/cf561b286cc5fab0a28c876542f4dc8d.png)
116/3 a) 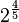
b) 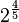
c) 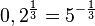 - Die Basis soll eine natürliche Zahl sein!
- Die Basis soll eine natürliche Zahl sein!
d) 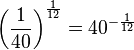
Hier kann man das Ergebnis noch teilweise radizieren. Es ist 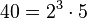 , also
, also 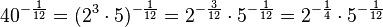
e) 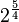
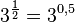
a) 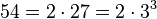 . Damit ist
. Damit ist ![\sqrt [3]{54}=\sqrt [3]{3^3\cdot 2}=3\sqrt [3]{2}](/images/math/3/1/f/31facb575e517dd777da79c6f40a6157.png)
b) 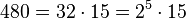 . Damit ist
. Damit ist ![\sqrt [5]{480}=2\sqrt [5]{15}](/images/math/8/8/5/88584edec33b66ed54710585a04fc5c3.png)
c) 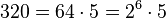 Damit ist
Damit ist ![\sqrt[3]{320}=\sqrt[3]{2^6\cdot 5}=2^2\cdot \sqrt[3]{5}=4\sqrt[3]{5}](/images/math/6/d/4/6d4088bdbf800d6ac62fa9f343a1b395.png)
d) 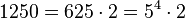 . Damit ist
. Damit ist ![\sqrt [4]{1250}=\sqrt [4]{5^4\cdot 2}=5\sqrt[4]{2}](/images/math/1/e/8/1e83dbf593621549a74b8e34efc4abb0.png)
e) 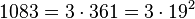 . Damit ist
. Damit ist 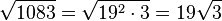
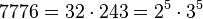 . Damit ist
. Damit ist ![\sqrt [4]{7776}=\sqrt [4]{2^5\cdot 3^5}=2\cdot3\cdot\sqrt[5]{2\cdot 3}=6\sqrt[4]{6}](/images/math/d/2/8/d284f14e400c51f49d0196fbc3d136ab.png)
a) ![3^{\frac{1}{2}}\cdot 3^{\frac{1}{3}}=3^{\frac{3+2}{6}}=3^{\frac{5}{6}}=\sqrt[6]{3^5}=\sqrt[6]{243}](/images/math/9/0/0/900f772bd2b801c5d01387df4b1add4a.png) ;
;
![2^{\frac{3}{5}}\cdot 2^{-\frac{4}{5}}=2^{\frac{3-4}{5}}=2^{-\frac{1}{5}}=\sqrt[5]{0,5}](/images/math/f/7/b/f7b16828f553e367e1135a0ab52ae46c.png)
... = 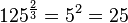
... = ![a^{\frac{1}{4}+\frac{1}{12}}=a^{\frac{4}{12}}=a^{\frac{1}{3}}=\sqrt [3]{a}](/images/math/5/a/d/5ad53429004fedaa9fa093e8929b5af5.png)
b) 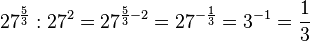
![81^{1,5}:81^{1,25}=81^{1,5-1,25}=81^{0,25}=81^{\frac{1}{4}}=\sqrt [4]{3^4}=3](/images/math/7/6/5/765584010fba168a90a19fc6e4caa1e6.png)
... = 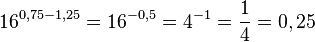
... = 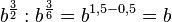
c) 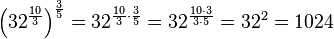
... = ![64^{\frac{1\cdot 21}{114\cdot 4}}=64^{\frac{3}{8}}=\left ( 2^6 \right )^{\frac{3}{8}}=2^{6\cdot \frac{3}{8}}=2^{\frac{9}{4}}=\sqrt [4]{2^9}=\sqrt [4]{512}](/images/math/9/5/b/95b56a1f630f803731e42aee782737a6.png)
... = 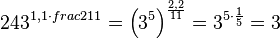
... = ![a^{\frac{3}{4}}=\sqrt[4]{a^3}](/images/math/f/0/d/f0d859f198e013b61cc3cc69f9cb4fc5.png) - in der Klammer steht eine Wurzel und Wurzelziehen und Quadrieren heben sich auf!
- in der Klammer steht eine Wurzel und Wurzelziehen und Quadrieren heben sich auf!
d) 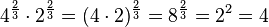
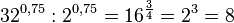
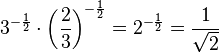
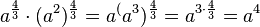
e) ![\sqrt [3]{4} \cdot \sqrt [4]{4} =4^{\frac{1}{3}+\frac{1}{4}}=4^{\frac{7}{12}}=(2^2)^{\frac{7}{12}}=2^{2\cdot \frac{7}{12}} =2^{\frac{7}{6}}=\sqrt [6]{2^7}=\sqrt [6]{128}](/images/math/2/6/b/26b7d813be4a51159e9d489b54774f89.png)
... = 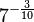
... = 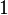
... = 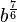
f) ... = ![\sqrt [3]{18}=18^{\frac{1}{3}}](/images/math/e/6/f/e6f3893482d630cdaa7d1c1471d15d6a.png)
... = ![\sqrt [5]{243} = 3](/images/math/e/0/5/e05396213ebba89eaebcb52448c6f6cd.png)
... = ![\sqrt [4]{16}=2](/images/math/3/b/2/3b211dc1ffaf85781b3a0af73ae4cd6a.png)
... = 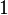 - es ist stets
- es ist stets 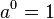
g) ![\sqrt {\sqrt [3]{6}}=\left ( 6^{\frac{1}{3}} \right ) ^{\frac{1}{2}}=6^{\frac{1}{3}\cdot \frac{1}{2}}=6^{\frac{1}{6}}=\sqrt [6]{6}](/images/math/6/9/1/691b83e98bcdb581a1c0dd53a72b4b9b.png)
... = 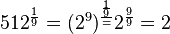
... = ![(2^5)^{\frac{1}{20}}=2^{5\cdot \frac{1}{20}}=2^{\frac{1}{4}}=\sqrt [4]{2}](/images/math/d/5/b/d5b0b7dd774f7de49386cb1fda1e3385.png)
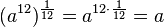
117/9
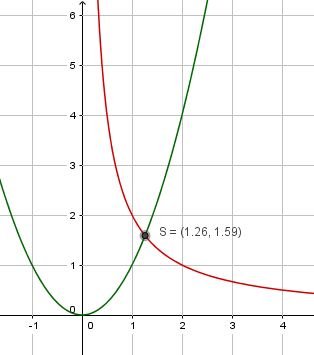
a) Ein Kubikmeterwürfel hat das Volumen V = 1 m3. Ein Würfel der doppeltes Volumen hat hat das Volumen Vneu = 2 m3 und die Seitenlänge ![b = \sqrt [3]{2} m \approx 1,26](/images/math/d/4/7/d4776aaf8773cd764f0608a7ff6c9572.png)
b) TR liefert 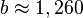
c) ---
e) In Aufgabe a) wird die Seitenlänge a = 1m zu Grunde gelegt und man rechnet die Seitenlänge des neuen Altars aus.
Bei b) wird die Gleichung x3 = 2, die sich algebraisch als Lösung ergibt nach x aufgelöst und man erhält die Seitenlänge des "doppelten Kubikmeterwürfels".
Bei d) führt die Frage nach dem Schnittpunkt auf die Gleichung x3 = 2, die man in b) schon gelöst hat.
Allgemein kann man die Problemstellung lösen. Der "alte Altar" hat das Volumen V = a3. Der neue Altar mit Seitenlänge b soll doppeltes Volumen haben, also V = b3 = 2 · a3. Dies führt zur Gleichung b3 = 2 · a3 und zur Lösung ![b = \sqrt [3] {2} \cdot a](/images/math/f/a/e/fae1a693e9ce1a22098143d061d65e8b.png) .
.

![\sqrt[n]{a}](/images/math/9/a/2/9a2b6d33f3d62a1e8bd99c76f3cb79f5.png) kann man auch eine Potenz
kann man auch eine Potenz 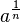 schreiben. Es ist für a
schreiben. Es ist für a 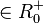 , n
, n 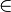 N \ {1}
N \ {1}
![\sqrt[n]{a^m}=a^{\frac{m}{n}}](/images/math/8/5/c/85c88b44eee019603a6e7884c34a8050.png)
![\sqrt[n]{a^n}=a^{\frac{n}{n}}=a^1=a](/images/math/9/b/d/9bd6f13f768b895069a041089c026c05.png)
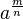 hat man zwei mögliche Wurzelschreibweisen:
hat man zwei mögliche Wurzelschreibweisen: 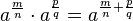
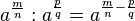
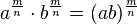
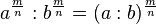
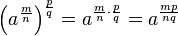
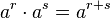
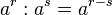
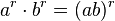
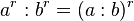
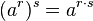
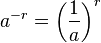 ist.
ist.
![a^{\frac{m}{n}}=\sqrt [n]{a^m}=(\sqrt [n] {a})^m](/images/math/0/3/6/0367448ffa6fd36c69b124002a162775.png) . Hier sieht man, dass der Nenner n des Exponenten für die Wurzel zuständig ist und der Zähler m potenziert.
. Hier sieht man, dass der Nenner n des Exponenten für die Wurzel zuständig ist und der Zähler m potenziert. 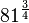 sieht man, dass oft der zweite Weg der günstigere ist:
sieht man, dass oft der zweite Weg der günstigere ist:![81^{\frac{3}{4}}=\sqrt[4]{81^3}=\sqrt[4]{531441} = 27](/images/math/2/3/4/234ae2422f7782b98a662533c7b4cc83.png) Hier hilft nur noch der Taschenrechner, das ist im Kopf nicht machbar!
Hier hilft nur noch der Taschenrechner, das ist im Kopf nicht machbar!![81^{\frac{3}{4}}=(\sqrt[4]{81})^3 = 3^3 = 27](/images/math/a/6/2/a62c1d001d4e7cdadd8273325eae3e27.png) Hier blieben die Zahlen klein und überschaubar.
Hier blieben die Zahlen klein und überschaubar.
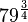 ist, dann weiß man, dass 79 eine Primzahl ist und es ist keine Wurzel möglich. Dann lässt man den Term auch gleich als Ergebnis
ist, dann weiß man, dass 79 eine Primzahl ist und es ist keine Wurzel möglich. Dann lässt man den Term auch gleich als Ergebnis ![79^{\frac{3}{4}}=\sqrt[4]{79^3} = \sqrt[4]{493039}](/images/math/a/b/6/ab66a6a05d0f91cfe7380dba8dfa7839.png) , das bringt aber nichts. Einzig einen Näherungswert mit dem Taschenrechner berechnen ist eventuell sinnvoll
, das bringt aber nichts. Einzig einen Näherungswert mit dem Taschenrechner berechnen ist eventuell sinnvoll 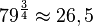 .
.
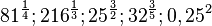
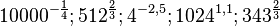
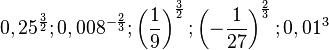
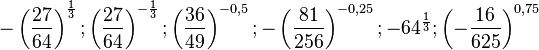
 und damit kann man vielleicht leichter weitermachen.
und damit kann man vielleicht leichter weitermachen.